Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 51643 by Tawa1 last updated on 29/Dec/18

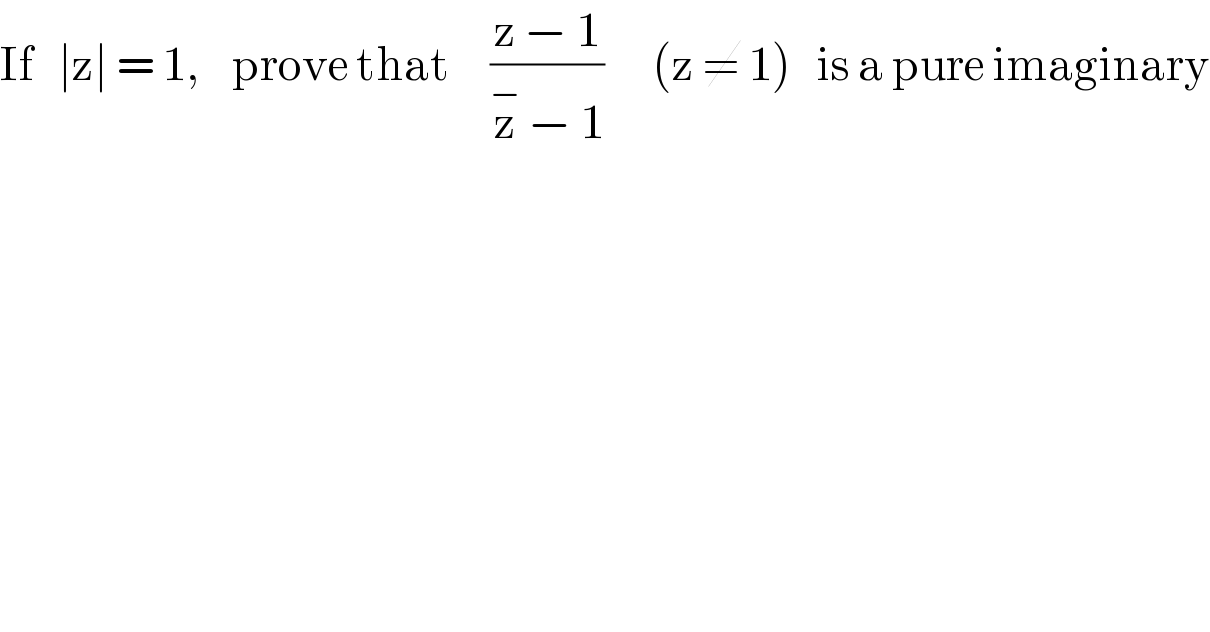
If ∣z∣ = 1, prove that ((z − 1)/(z^− − 1)) (z ≠ 1) is a pure imaginary

$$\mathrm{If}\:\:\:\mid\mathrm{z}\mid\:=\:\mathrm{1},\:\:\:\:\mathrm{prove}\:\mathrm{that}\:\:\:\:\:\frac{\mathrm{z}\:−\:\mathrm{1}}{\overset{−} {\mathrm{z}}\:−\:\mathrm{1}}\:\:\:\:\:\:\left(\mathrm{z}\:\neq\:\mathrm{1}\right)\:\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{pure}\:\mathrm{imaginary} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 29/Dec/18

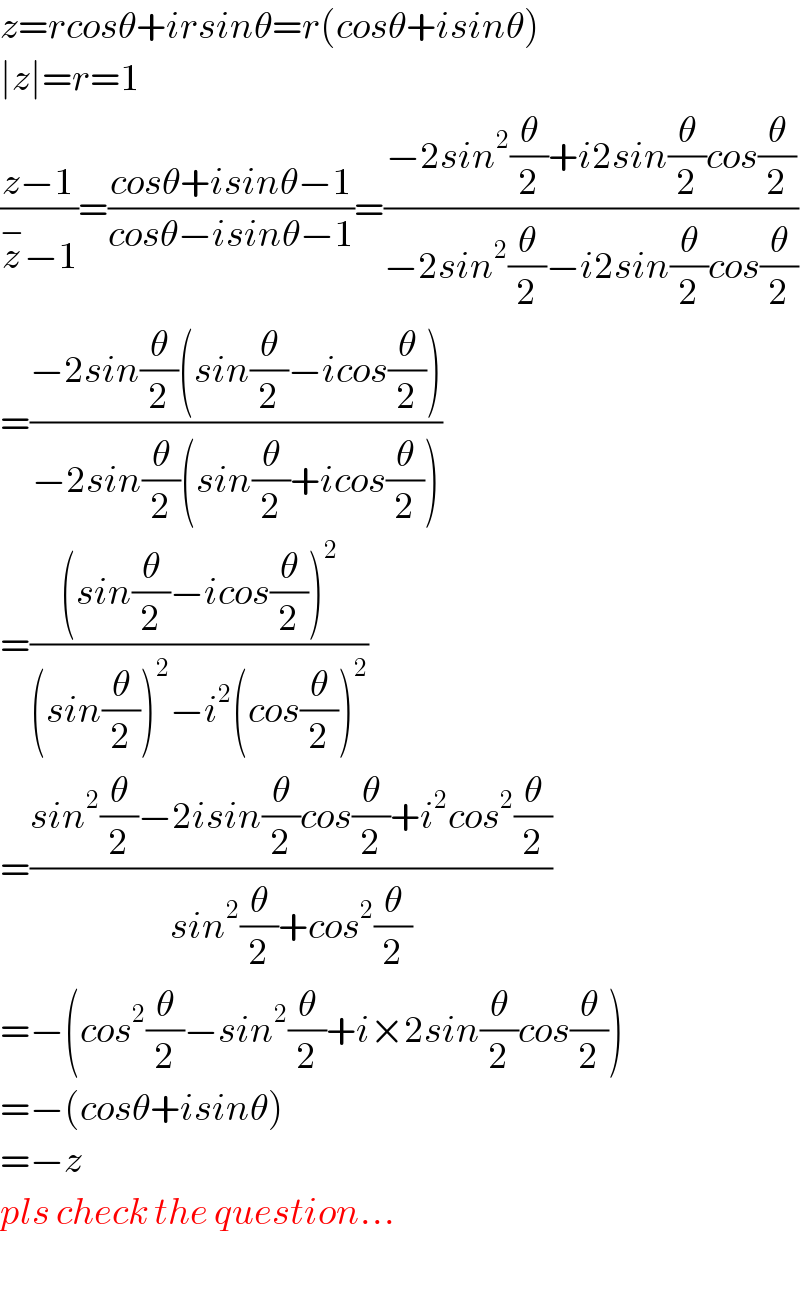
z=rcosθ+irsinθ=r(cosθ+isinθ) ∣z∣=r=1 ((z−1)/(z^− −1))=((cosθ+isinθ−1)/(cosθ−isinθ−1))=((−2sin^2 (θ/2)+i2sin(θ/2)cos(θ/2))/(−2sin^2 (θ/2)−i2sin(θ/2)cos(θ/2))) =((−2sin(θ/2)(sin(θ/2)−icos(θ/2)))/(−2sin(θ/2)(sin(θ/2)+icos(θ/2)))) =(((sin(θ/2)−icos(θ/2))^2 )/((sin(θ/2))^2 −i^2 (cos(θ/2))^2 )) =((sin^2 (θ/2)−2isin(θ/2)cos(θ/2)+i^2 cos^2 (θ/2))/(sin^2 (θ/2)+cos^2 (θ/2))) =−(cos^2 (θ/2)−sin^2 (θ/2)+i×2sin(θ/2)cos(θ/2)) =−(cosθ+isinθ) =−z pls check the question...

$${z}={rcos}\theta+{irsin}\theta={r}\left({cos}\theta+{isin}\theta\right) \\ $$$$\mid{z}\mid={r}=\mathrm{1} \\ $$$$\frac{{z}−\mathrm{1}}{\overset{−} {{z}}−\mathrm{1}}=\frac{{cos}\theta+{isin}\theta−\mathrm{1}}{{cos}\theta−{isin}\theta−\mathrm{1}}=\frac{−\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+{i}\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}{cos}\frac{\theta}{\mathrm{2}}}{−\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−{i}\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}{cos}\frac{\theta}{\mathrm{2}}} \\ $$$$=\frac{−\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}\left({sin}\frac{\theta}{\mathrm{2}}−{icos}\frac{\theta}{\mathrm{2}}\right)}{−\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}\left({sin}\frac{\theta}{\mathrm{2}}+{icos}\frac{\theta}{\mathrm{2}}\right)} \\ $$$$=\frac{\left({sin}\frac{\theta}{\mathrm{2}}−{icos}\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} }{\left({sin}\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} −{i}^{\mathrm{2}} \left({cos}\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−\mathrm{2}{isin}\frac{\theta}{\mathrm{2}}{cos}\frac{\theta}{\mathrm{2}}+{i}^{\mathrm{2}} {cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$$=−\left({cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+{i}×\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}{cos}\frac{\theta}{\mathrm{2}}\right) \\ $$$$=−\left({cos}\theta+{isin}\theta\right) \\ $$$$=−{z} \\ $$$${pls}\:{check}\:{the}\:{question}... \\ $$$$ \\ $$

Commented by Tawa1 last updated on 29/Dec/18

God bless you sir. The question is not true sir ?

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{The}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{true}\:\mathrm{sir}\:? \\ $$

Commented by peter frank last updated on 29/Dec/18

⇒ ((z+1)/(z−1)) i think

$$\Rightarrow\:\frac{{z}+\mathrm{1}}{{z}−\mathrm{1}}\:\:\:\:{i}\:{think} \\ $$

Answered by peter frank last updated on 29/Dec/18

((z+1)/(z−1)) z=x+iy z^− =x−iy ((x+iy−1)/(x−iy−1)) (((x+1)+iy)/((x−1)−iy)) [ (((x+1)+iy)/((x−1)−iy))]×[(((x−1)+iy)/((x−1)+iy ))] ((x^2 +y^2 −1)/(x^2 +y^2 −2x))+((2xi)/(x^2 +y^2 −2x)) pure imaginary ((x^2 +y^2 −1)/(x^2 +y^2 −2x))=0 x^2 +y^2 −1=0 x^2 +y^2 =1 ∣x+iy∣=1 ∣z∣=1

$$\frac{{z}+\mathrm{1}}{{z}−\mathrm{1}} \\ $$$${z}={x}+{iy} \\ $$$$\overset{−} {{z}}={x}−{iy} \\ $$$$\frac{{x}+{iy}−\mathrm{1}}{{x}−{iy}−\mathrm{1}} \\ $$$$\:\frac{\left({x}+\mathrm{1}\right)+{iy}}{\left({x}−\mathrm{1}\right)−{iy}} \\ $$$$\left[\:\frac{\left({x}+\mathrm{1}\right)+{iy}}{\left({x}−\mathrm{1}\right)−{iy}}\right]×\left[\frac{\left({x}−\mathrm{1}\right)+{iy}}{\left({x}−\mathrm{1}\right)+{iy}\:}\right] \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}}+\frac{\mathrm{2}{xi}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}} \\ $$$${pure}\:{imaginary} \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mid{x}+{iy}\mid=\mathrm{1} \\ $$$$\mid{z}\mid=\mathrm{1} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 29/Dec/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com