Question and Answers Forum
Question Number 51774 by ajfour last updated on 30/Dec/18

Commented by ajfour last updated on 30/Dec/18
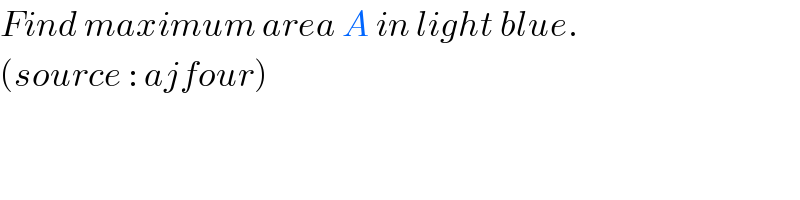
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18

Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
![area of OABCDA is=2[(1/2)×h×b+(1/2)×k×a] =hb+ka area if pinnk circle sector=(b^2 /2)×(π−2α) area of yelolow circle sector=(a^2 /2)×(π−2β) 2α+2β=(π/2) α+β=(π/4) area of light blue area hb+ka−[(π/2)(a^2 +b^2 )−(a^2 β+b^2 α)] to my view...tangent from point o to circle radius b...tangent from o to circle radis a should be equal ldngth... so h=k tanα=(b/h) α=tan^(−1) ((b/h)) tanβ=(a/k)=(a/h) β=tan^(−1) ((a/h)) tan(α+β)=((tanα+tanβ)/(1−tanαtanβ))=(((b/h)+(a/h))/(1−((ab)/h^2 )))=(((a+b)/h)/(1−((ab)/h^2 )))=1 ((a+b)/h)=1−((ab)/h^2 ) (a+b)h=h^2 −ab h^2 −h(a+b)−ab=0 h=(((a+b)±(√((a+b)^2 +4ab)))/2) h=(((a+b)+(√((a+b)^2 +4ab)))/2)=L(say) so light blue area hb+ka−[(π/2)(a^2 +b^2 )−(a^2 β+b^2 α)] =L(a+b)−[(π/2)(a^2 +b^2 )−{a^2 tan^(−1) ((a/L))+b^2 tan^(−1) ((b/L))] where L=f(a,b) pls chek upto this step...](Q51780.png)
Commented by ajfour last updated on 30/Dec/18
Answered by mr W last updated on 30/Dec/18

Commented by mr W last updated on 30/Dec/18
![A_(blue) =[a+(a+b)cos α][b+(a+b)sin α]−(((a+b)^2 sin α cos α)/2)+((αa^2 )/2)+((((π/2)−α)b^2 )/2)−((πa^2 )/2)−((πb^2 )/2) A_(blue) =(a+b)[(a sin α+b cos α)+(((a+b)sin 2α)/4)+((α(a−b))/2)]+ab−((πa^2 )/2)−((πb^2 )/4) ...(ii) (dA_(blue) /dα)=0 ⇒a cos α−b sin α+(((a+b)cos 2α)/2)+((a−b)/2)=0 ⇒2(a cos α−b sin α)+(a+b)cos 2α=b−a let (b/a)=μ, t=tan (α/2) ⇒cos α(1+cos α)=μ sin α(1+sin α) ⇒μ=((cos α(1+cos α))/(sin α(1+sin α)))=((1−t)/(t(1+t))) μt^2 +(μ+1)t−1=0 t=tan (α/2)=(((√(μ^2 +6μ+1))−μ−1)/(2μ)) ⇒α=2 tan^(−1) (((√(μ^2 +6μ+1))−μ−1)/(2μ)) ⇒max. A_(blue) from (ii)](Q51787.png)
Commented by ajfour last updated on 30/Dec/18
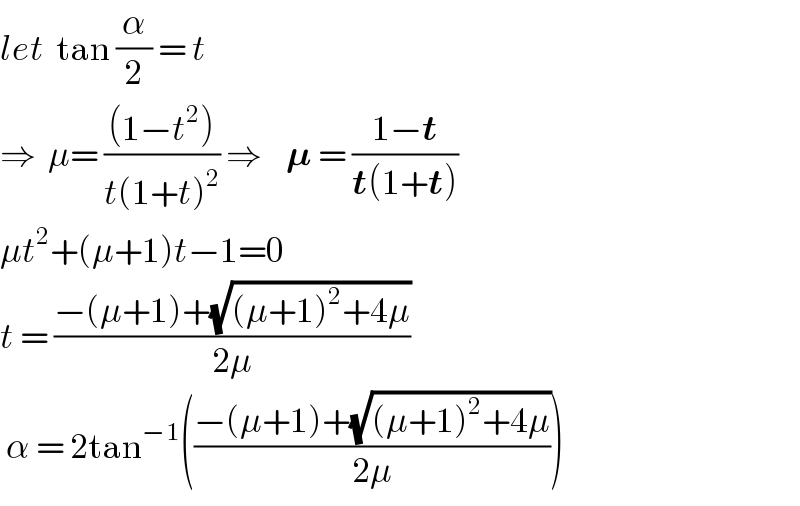
Commented by ajfour last updated on 30/Dec/18
Commented by mr W last updated on 30/Dec/18