Question Number 51933 by Tawa1 last updated on 01/Jan/19
$$\mathrm{If}\:\:\mathrm{p}\:=\:\mathrm{cos}\:\theta\:+\:\mathrm{i}\:\mathrm{sin}\:\theta\:\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\:\:\:\mathrm{q}\:\:=\:\:\mathrm{cos}\:\phi\:+\:\mathrm{i}\:\mathrm{sin}\:\phi \\ $$$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{p}\:+\:\mathrm{q}\right)\left(\mathrm{pq}\:−\:\mathrm{1}\right)}{\left(\mathrm{p}\:−\:\mathrm{q}\right)\left(\mathrm{pq}\:+\:\mathrm{1}\right)}\:\:=\:\:\frac{\mathrm{sin}\:\theta\:+\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\theta\:−\:\mathrm{sin}\:\phi} \\ $$
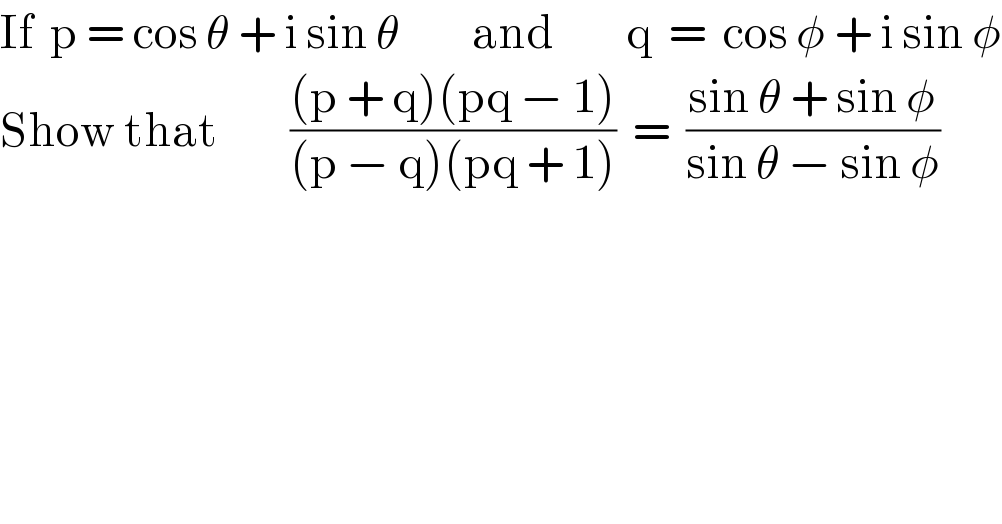
Commented by peter frank last updated on 01/Jan/19
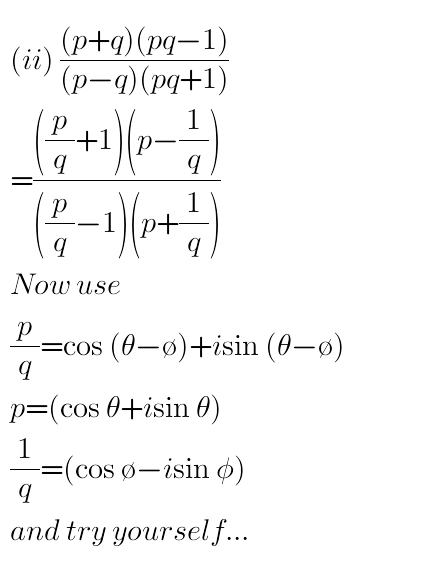
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jan/19
![p=e^(iθ) q=e^(i∅) LHS (((p+q)(pq−1))/((p−q)((pq+1))) ((((p/q)+1))/(pq+1))×((pq−1)/((p/q)−1)) =((e^(i(θ−∅)) +1)/(e^(i(θ+∅)) +1))×((e^(i(θ+∅)) −1)/(e^(i(θ−∅)) −1)) =((cos(θ−∅)+isin(θ−∅)+1)/(cos(θ+∅)+isin(θ+∅)+1))×((cos(θ+∅)+isin(θ+∅)−1)/(cos(θ−∅)+isin(θ−∅)−1)) =((2cos^2 ((θ−∅)/2)+i2sin((θ−∅)/2)cos((θ−∅)/2))/(2cos^2 ((θ+∅)/2)+i2sin((θ+∅)/2)cos((θ+φ)/2)))×((1−cos(θ+∅)−isin(θ+φ))/(1−cos(θ−∅)−isin(θ−∅))) =((2cos((θ−∅)/2)[cos((θ−∅)/2)+isin((θ−∅)/2)])/(2cos((θ+∅)/2)[cos((θ+∅)/2)+isin((θ+∅)/2)]))×((2sin^2 ((θ+∅)/2)−2isin((θ+φ)/2)cos((θ+∅)/2))/(2sin^2 ((θ−φ)/2)−2isin((θ−∅)/2)cos((θ−φ)/2))) =((cos((θ−∅)/2))/(cos((θ+∅)/2)))×e^(i(((θ−∅)/2))−i(((θ+∅)/2))) ×((2sin((θ+∅)/2))/(2sin((θ−φ)/2)))×(([sin((θ+∅)/2)−icos((θ+∅)/2)])/([sin((θ−∅)/2)−icos((θ−∅)/2)])) ((tan((θ+φ)/2))/(tan((θ−φ)/2)))×e^(i(((θ−φ−θ−φ)/2))) ×(e^(−i[(π/2)−(((θ+φ)/2))]) /e^(−i[(π/2)−(((θ−∅)/2))]) ) =((tan((θ+φ)/2))/(tan((θ−∅)/2)))×e^(−iφ) ×e^(−((iπ)/2)+i(((θ+φ))/2)+((iπ)/2)−i(((θ−∅)/2))) =((tan((θ+∅)/2))/(tan((θ−φ)/2)))×e^(−i∅) ×e^(i(((θ+∅−θ+φ)/2))) =((tan((θ+∅)/2))/(tan((θ−∅)/2)))×e^(−i∅+i∅) =((2sin((θ+∅)/2)cos((θ−∅)/2))/(2sin((θ−∅)/2)cos((θ+∅)/2))) =((sinθ+sin∅)/(sinθ−sin∅))](Q51936.png)
$${p}={e}^{{i}\theta} \:\:\:{q}={e}^{{i}\emptyset} \\ $$$${LHS} \\ $$$$\frac{\left({p}+{q}\right)\left({pq}−\mathrm{1}\right)}{\left({p}−{q}\right)\left(\left({pq}+\mathrm{1}\right)\right.} \\ $$$$\frac{\left(\frac{{p}}{{q}}+\mathrm{1}\right)}{{pq}+\mathrm{1}}×\frac{{pq}−\mathrm{1}}{\frac{{p}}{{q}}−\mathrm{1}} \\ $$$$=\frac{{e}^{{i}\left(\theta−\emptyset\right)} +\mathrm{1}}{{e}^{{i}\left(\theta+\emptyset\right)} +\mathrm{1}}×\frac{{e}^{{i}\left(\theta+\emptyset\right)} −\mathrm{1}}{{e}^{{i}\left(\theta−\emptyset\right)} −\mathrm{1}} \\ $$$$=\frac{{cos}\left(\theta−\emptyset\right)+{isin}\left(\theta−\emptyset\right)+\mathrm{1}}{{cos}\left(\theta+\emptyset\right)+{isin}\left(\theta+\emptyset\right)+\mathrm{1}}×\frac{{cos}\left(\theta+\emptyset\right)+{isin}\left(\theta+\emptyset\right)−\mathrm{1}}{{cos}\left(\theta−\emptyset\right)+{isin}\left(\theta−\emptyset\right)−\mathrm{1}} \\ $$$$=\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta−\emptyset}{\mathrm{2}}+{i}\mathrm{2}{sin}\frac{\theta−\emptyset}{\mathrm{2}}{cos}\frac{\theta−\emptyset}{\mathrm{2}}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta+\emptyset}{\mathrm{2}}+{i}\mathrm{2}{sin}\frac{\theta+\emptyset}{\mathrm{2}}{cos}\frac{\theta+\phi}{\mathrm{2}}}×\frac{\mathrm{1}−{cos}\left(\theta+\emptyset\right)−{isin}\left(\theta+\phi\right)}{\mathrm{1}−{cos}\left(\theta−\emptyset\right)−{isin}\left(\theta−\emptyset\right)} \\ $$$$=\frac{\mathrm{2}{cos}\frac{\theta−\emptyset}{\mathrm{2}}\left[{cos}\frac{\theta−\emptyset}{\mathrm{2}}+{isin}\frac{\theta−\emptyset}{\mathrm{2}}\right]}{\mathrm{2}{cos}\frac{\theta+\emptyset}{\mathrm{2}}\left[{cos}\frac{\theta+\emptyset}{\mathrm{2}}+{isin}\frac{\theta+\emptyset}{\mathrm{2}}\right]}×\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta+\emptyset}{\mathrm{2}}−\mathrm{2}{isin}\frac{\theta+\phi}{\mathrm{2}}{cos}\frac{\theta+\emptyset}{\mathrm{2}}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta−\phi}{\mathrm{2}}−\mathrm{2}{isin}\frac{\theta−\emptyset}{\mathrm{2}}{cos}\frac{\theta−\phi}{\mathrm{2}}} \\ $$$$=\frac{{cos}\frac{\theta−\emptyset}{\mathrm{2}}}{{cos}\frac{\theta+\emptyset}{\mathrm{2}}}×{e}^{{i}\left(\frac{\theta−\emptyset}{\mathrm{2}}\right)−{i}\left(\frac{\theta+\emptyset}{\mathrm{2}}\right)} ×\frac{\mathrm{2}{sin}\frac{\theta+\emptyset}{\mathrm{2}}}{\mathrm{2}{sin}\frac{\theta−\phi}{\mathrm{2}}}×\frac{\left[{sin}\frac{\theta+\emptyset}{\mathrm{2}}−{icos}\frac{\theta+\emptyset}{\mathrm{2}}\right]}{\left[{sin}\frac{\theta−\emptyset}{\mathrm{2}}−{icos}\frac{\theta−\emptyset}{\mathrm{2}}\right]} \\ $$$$\frac{{tan}\frac{\theta+\phi}{\mathrm{2}}}{{tan}\frac{\theta−\phi}{\mathrm{2}}}×{e}^{{i}\left(\frac{\theta−\phi−\theta−\phi}{\mathrm{2}}\right)} ×\frac{{e}^{−{i}\left[\frac{\pi}{\mathrm{2}}−\left(\frac{\theta+\phi}{\mathrm{2}}\right)\right]} }{{e}^{−{i}\left[\frac{\pi}{\mathrm{2}}−\left(\frac{\theta−\emptyset}{\mathrm{2}}\right)\right]} } \\ $$$$=\frac{{tan}\frac{\theta+\phi}{\mathrm{2}}}{{tan}\frac{\theta−\emptyset}{\mathrm{2}}}×{e}^{−{i}\phi} ×{e}^{−\frac{{i}\pi}{\mathrm{2}}+{i}\frac{\left(\theta+\phi\right)}{\mathrm{2}}+\frac{{i}\pi}{\mathrm{2}}−{i}\left(\frac{\theta−\emptyset}{\mathrm{2}}\right)} \\ $$$$=\frac{{tan}\frac{\theta+\emptyset}{\mathrm{2}}}{{tan}\frac{\theta−\phi}{\mathrm{2}}}×{e}^{−{i}\emptyset} ×{e}^{{i}\left(\frac{\theta+\emptyset−\theta+\phi}{\mathrm{2}}\right)} \\ $$$$=\frac{{tan}\frac{\theta+\emptyset}{\mathrm{2}}}{{tan}\frac{\theta−\emptyset}{\mathrm{2}}}×{e}^{−{i}\emptyset+{i}\emptyset} \\ $$$$=\frac{\mathrm{2}{sin}\frac{\theta+\emptyset}{\mathrm{2}}{cos}\frac{\theta−\emptyset}{\mathrm{2}}}{\mathrm{2}{sin}\frac{\theta−\emptyset}{\mathrm{2}}{cos}\frac{\theta+\emptyset}{\mathrm{2}}} \\ $$$$=\frac{{sin}\theta+{sin}\emptyset}{{sin}\theta−{sin}\emptyset} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 01/Jan/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}.\: \\ $$
Answered by $@ty@m last updated on 01/Jan/19
$${see}\:{my}\:{solution}\:{to} \\ $$$${Q}.\:{No}.\:\mathrm{51905} \\ $$
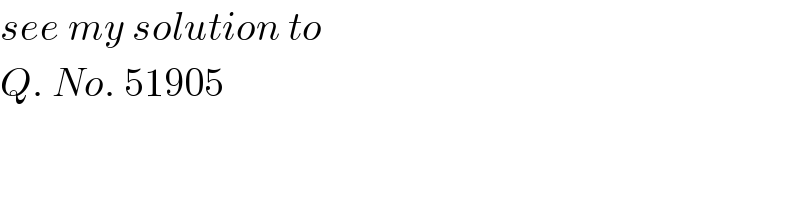
Commented by Tawa1 last updated on 01/Jan/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$