Question Number 51942 by mr W last updated on 01/Jan/19
Commented by mr W last updated on 01/Jan/19
$${Find}\:{the}\:{sum}\:{of}\:{all}\:{corner}\:{angles} \\ $$$${of}\:{a}\:{n}−{corner}\:{star}. \\ $$$$\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} +\alpha_{\mathrm{3}} +...+\alpha_{{n}} =? \\ $$$$\left({n}={odd}\:{integer},\:{n}\geqslant\mathrm{5}\right) \\ $$
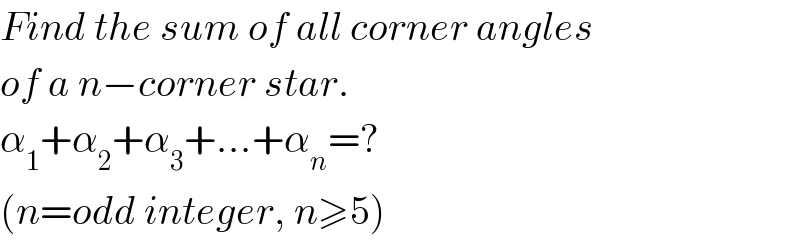
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jan/19
Commented by mr W last updated on 01/Jan/19
$${thank}\:{you}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jan/19
![n sided star form n sided polygon. The sum of internal angles of n sided polygon x_1 +x_2 +x_3 +...+x_n =nπ−2π we have to find the value of α_1 +α_2 +α_3 +...α_n now consider any one triangle α_1 +a_1 +a_2 =π a_1 +x_1 =π a_1 =π−x_1 a_2 +x_2 =π a_2 =π−x_2 so α_1 +π−x_1 +π−x_2 =π α_1 =x_1 +x_2 −π α_2 =x_2 +x_3 −π ..... ..... α_1 +α_2 +α_3 +....+α_n =2(x_1 +x_2 +x_3 +..+x_n )−nπ so α_1 +α_2 +...+α_n =2[nπ−2π]−nπ =nπ−4π pls check i have derived the formula...](Q51958.png)
$${n}\:{sided}\:{star}\:{form}\:{n}\:{sided}\:{polygon}. \\ $$$${The}\:{sum}\:{of}\:{internal}\:{angles}\:{of}\:{n}\:{sided}\:{polygon} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +...+{x}_{{n}} ={n}\pi−\mathrm{2}\pi \\ $$$${we}\:{have}\:{to}\:{find}\:{the}\:{value}\:{of} \\ $$$$\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} +\alpha_{\mathrm{3}} +...\alpha_{{n}} \\ $$$${now}\:{consider}\:{any}\:{one}\:{triangle} \\ $$$$\alpha_{\mathrm{1}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} =\pi \\ $$$${a}_{\mathrm{1}} +{x}_{\mathrm{1}} =\pi\:\:{a}_{\mathrm{1}} =\pi−{x}_{\mathrm{1}} \\ $$$${a}_{\mathrm{2}} +{x}_{\mathrm{2}} =\pi\:\:\:{a}_{\mathrm{2}} =\pi−{x}_{\mathrm{2}} \\ $$$${so}\:\alpha_{\mathrm{1}} +\pi−{x}_{\mathrm{1}} +\pi−{x}_{\mathrm{2}} =\pi \\ $$$$\alpha_{\mathrm{1}} ={x}_{\mathrm{1}} +{x}_{\mathrm{2}} −\pi \\ $$$$\alpha_{\mathrm{2}} ={x}_{\mathrm{2}} +{x}_{\mathrm{3}} −\pi \\ $$$$..... \\ $$$$..... \\ $$$$\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} +\alpha_{\mathrm{3}} +....+\alpha_{{n}} =\mathrm{2}\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +..+{x}_{{n}} \right)−{n}\pi \\ $$$${so}\: \\ $$$$\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} +...+\alpha_{{n}} =\mathrm{2}\left[{n}\pi−\mathrm{2}\pi\right]−{n}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={n}\pi−\mathrm{4}\pi \\ $$$${pls}\:{check}\:{i}\:{have}\:{derived}\:{the}\:{formula}... \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 01/Jan/19
$$\Sigma\alpha=\pi\:! \\ $$$${consider}\:{the}\:{case}\:{that}\:{the}\:{corners}\:{are} \\ $$$${on}\:{a}\:{circle},\:{then}\:{we}\:{have} \\ $$$${sum}\:{of}\:{all}\:{central}\:{angles}=\Sigma\left(\mathrm{2}\alpha\right)=\mathrm{2}\pi \\ $$$$\Rightarrow\Sigma\alpha=\pi \\ $$
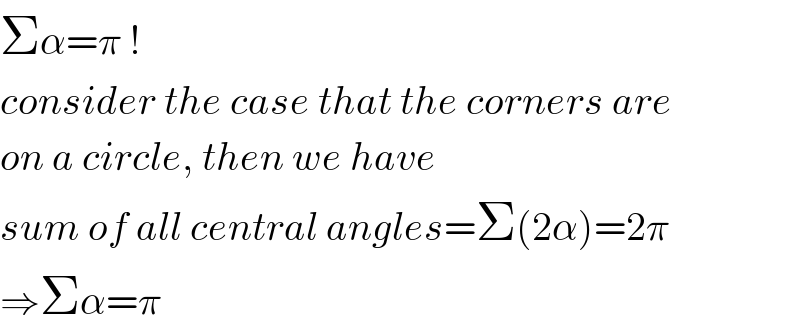
Answered by mr W last updated on 01/Jan/19
Commented by mr W last updated on 01/Jan/19
$$\left(\alpha_{\mathrm{1}} +\beta_{\mathrm{1}} \right)+\left(\alpha_{\mathrm{2}} +\gamma_{\mathrm{2}} \right)+\alpha_{{n}−\mathrm{2}} =\pi\:\:\:\left({triangle}\right) \\ $$$$\Sigma\alpha+\Sigma\beta+\Sigma\alpha+\Sigma\gamma+\Sigma\alpha={n}\pi \\ $$$$\mathrm{2}\Sigma\alpha+\left(\Sigma\alpha+\Sigma\beta+\Sigma\gamma\right)={n}\pi \\ $$$${since}\:\Sigma\alpha+\Sigma\beta+\Sigma\gamma=\left({n}−\mathrm{2}\right)\pi\:\:\:\left({n}−{side}\:{polygon}\right) \\ $$$$\Rightarrow\mathrm{2}\Sigma\alpha+\left({n}−\mathrm{2}\right)\pi={n}\pi \\ $$$$\Rightarrow\Sigma\alpha=\pi \\ $$$${this}\:{is}\:{independent}\:{from}\:{n}. \\ $$
Commented by mr W last updated on 02/Jan/19
$${yes}\:{sir}.\:{but}\:{here}\:{it}\:{doesn}'{t}\:{matter}\:{how} \\ $$$${we}\:{call}\:{it}. \\ $$
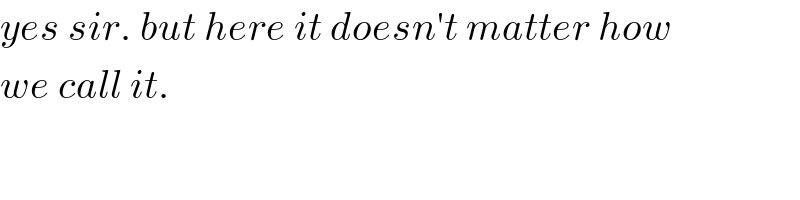
Commented by mr W last updated on 01/Jan/19
$${such}\:{stars}\:{can}\:{only}\:{have}\:{odd}\:{number} \\ $$$${of}\:{corners}.\:{they}\:{are}\:{no}\:``{normal}''\:{polygons},\:{but} \\ $$$${consist}\:{of}\:{diagonals}\:{of}\:{a}\:``{normal}''\:{polygon}\:{with} \\ $$$${odd}\:{number}\:{of}\:{sides}. \\ $$
Commented by mr W last updated on 01/Jan/19
