Question Number 51997 by maxmathsup by imad last updated on 01/Jan/19
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{xsint}}\:\:{with}\:{x}>−\mathrm{1} \\ $$ $$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({o}\right)\:,{f}\left(\mathrm{1}\right)\:{and}\:{f}\left(\mathrm{2}\right) \\ $$ $$\left.\mathrm{2}\right)\:{give}\:{f}\:{at}\:{form}\:{of}\:{function}\: \\ $$ $$ \\ $$
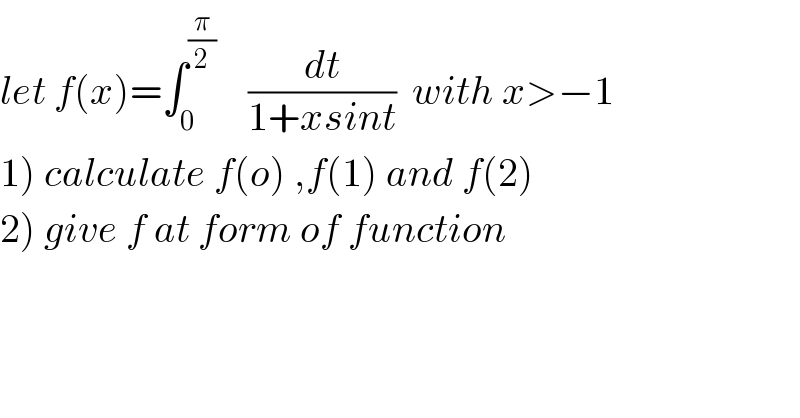
Commented bymaxmathsup by imad last updated on 02/Jan/19
![1) we have f(0)=∫_0 ^(π/2) dt =(π/2) f(1) =∫_0 ^(π/2) (dt/(1+sint)) =_(tan((t/2))=u) ∫_0 ^1 (1/(1+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^1 (du/(1+u^2 +2u)) =2∫_0 ^1 (du/((u+1)^2 )) =[−(2/(u+1))]_0 ^1 =−2((1/2) −1) =−1+2 =1 ⇒f(1)=1 f(2) =∫_0 ^(π/2) (dt/(1+2sint)) =_(tan((t/2))=u) ∫_0 ^1 (1/(1+2((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^1 (du/(1+u^2 +4u)) =2 ∫_0 ^1 (du/(u^2 +4u +1)) .roots of u^2 +4u +1 Δ^′ =2^2 −1 =3 ⇒u_1 =−2+(√3) and u_2 =−2−(√3) f(2) =2 ∫_0 ^1 (du/((u−u_1 )(u−u_2 ))) =(2/(u_1 −u_2 )) ∫_0 ^1 ((1/(u−u_1 )) −(1/(u−u_2 )))du =(2/(2(√3))) ∫_0 ^1 { (1/(u−u_1 )) −(1/(u−u_2 ))}du =(1/(√3))[ln∣((u−u_1 )/(u−u_2 ))∣]_0 ^1 =(1/(√3)){ln∣((1−u_1 )/(1−u_2 ))∣−ln∣(u_1 /u_2 )∣} =(1/(√3)){ln∣((3−(√3))/(3+(√3)))∣−ln∣((2−(√3))/(2+(√3)))∣ .](Q52055.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dt}\:=\frac{\pi}{\mathrm{2}} \\ $$ $${f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dt}}{\mathrm{1}+{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}} \\ $$ $$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left[−\frac{\mathrm{2}}{{u}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{1}\right)\:=−\mathrm{1}+\mathrm{2}\:=\mathrm{1}\:\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$ $${f}\left(\mathrm{2}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dt}}{\mathrm{1}+\mathrm{2}{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{4}{u}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{4}{u}\:+\mathrm{1}}\:\:.{roots}\:{of}\:{u}^{\mathrm{2}} \:+\mathrm{4}{u}\:+\mathrm{1} \\ $$ $$\Delta^{'} =\mathrm{2}^{\mathrm{2}} −\mathrm{1}\:\:=\mathrm{3}\:\Rightarrow{u}_{\mathrm{1}} =−\mathrm{2}+\sqrt{\mathrm{3}}\:\:{and}\:{u}_{\mathrm{2}} =−\mathrm{2}−\sqrt{\mathrm{3}} \\ $$ $${f}\left(\mathrm{2}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{\mathrm{2}}{{u}_{\mathrm{1}} −{u}_{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right){du} \\ $$ $$=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\:\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right\}{du}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left[{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left\{{ln}\mid\frac{\mathrm{1}−{u}_{\mathrm{1}} }{\mathrm{1}−{u}_{\mathrm{2}} }\mid−{ln}\mid\frac{{u}_{\mathrm{1}} }{{u}_{\mathrm{2}} }\mid\right\} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left\{{ln}\mid\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{3}+\sqrt{\mathrm{3}}}\mid−{ln}\mid\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}\mid\:.\right. \\ $$
Commented bymaxmathsup by imad last updated on 02/Jan/19
![2)changement tan((t/2))=u give f(x)=∫_0 ^1 (1/(1+x((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2∫_0 ^1 (du/(1+u^2 +2xu)) =2 ∫_0 ^1 (du/(u^2 +2xu +1)) let p(u)=u^2 +2xu +1 Δ^′ =x^2 −1 case1 Δ^′ >0 ⇔∣x∣>1 ⇒u_1 =−x+(√(x^2 −1)) and u_2 =−x−(√(x^2 −1)) ⇒f(x)=2 ∫_0 ^1 (du/((u−u_1 )(u−u_2 ))) =(2/(u_1 −u_2 ))∫_0 ^1 { (1/(u−u_1 )) −(1/(u−u_2 ))}du =(2/(2(√(1−x^2 )))) [ln∣((u−u_1 )/(u−u_2 ))∣]_0 ^1 =(1/(√(1−x^2 ))){ln∣((1−u_1 )/(1−u_2 ))∣−ln∣(u_1 /u_2 )∣} =(1/(√(1−x^2 ))){ln∣((1+x−(√(x^2 −1)))/(1+x+(√(x^2 −1))))∣−ln∣((x−(√(x^2 −1)))/(x+(√(x^2 −1))))∣} case2 Δ^′ <0 ⇔∣x∣<1 ⇒p(u)=u^2 +2xu +x^2 +1−x^2 =(u+x)^2 +1−x^2 we do the changement u+x=(√(1−x^2 ))α ⇒ f(x) =2 ∫_0 ^1 (du/((u+x)^2 +1−x^2 )) =2 ∫_(x/(√(1−x^2 ))) ^((1+x)/(√(1−x^2 ))) (((√(1−x^2 ))dα)/((1−x^2 )(1+α^2 ))) = (2/(√(1−x^2 ))) [arctan(α)]_(x/(√(1−x^2 ))) ^((1+x)/(√(1−x^2 ))) =(2/(√(1−x^2 ))) { arctan((√((1+x)/(1−x))))−arctan((x/(√(1−x^2 ))))} .](Q52070.png)
$$\left.\mathrm{2}\right){changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{xu}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}{xu}\:+\mathrm{1}}\:{let}\:{p}\left({u}\right)={u}^{\mathrm{2}} \:+\mathrm{2}{xu}\:+\mathrm{1} \\ $$ $$\Delta^{'} ={x}^{\mathrm{2}} −\mathrm{1} \\ $$ $${case}\mathrm{1}\:\:\Delta^{'} >\mathrm{0}\:\Leftrightarrow\mid{x}\mid>\mathrm{1}\:\:\Rightarrow{u}_{\mathrm{1}} =−{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:{and}\:{u}_{\mathrm{2}} =−{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$ $$\Rightarrow{f}\left({x}\right)=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{du}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{\mathrm{2}}{{u}_{\mathrm{1}} −{u}_{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\:\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right\}{du} \\ $$ $$=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\left[{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left\{{ln}\mid\frac{\mathrm{1}−{u}_{\mathrm{1}} }{\mathrm{1}−{u}_{\mathrm{2}} }\mid−{ln}\mid\frac{{u}_{\mathrm{1}} }{{u}_{\mathrm{2}} }\mid\right\} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left\{{ln}\mid\frac{\mathrm{1}+{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\mid−{ln}\mid\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\mid\right\} \\ $$ $${case}\mathrm{2}\:\:\Delta^{'} <\mathrm{0}\:\Leftrightarrow\mid{x}\mid<\mathrm{1}\:\Rightarrow{p}\left({u}\right)={u}^{\mathrm{2}} \:+\mathrm{2}{xu}\:+{x}^{\mathrm{2}} \:+\mathrm{1}−{x}^{\mathrm{2}} =\left({u}+{x}\right)^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{2}} \\ $$ $${we}\:{do}\:{the}\:{changement}\:{u}+{x}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\alpha\:\Rightarrow \\ $$ $${f}\left({x}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}+{x}\right)^{\mathrm{2}} \:+\mathrm{1}−{x}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}} ^{\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}} \:\:\:\:\:\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{d}\alpha}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$ $$=\:\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\left[{arctan}\left(\alpha\right)\right]_{\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}} ^{\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}} \:\:=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\left\{\:{arctan}\left(\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\right)−{arctan}\left(\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\right\}\:. \\ $$
Answered by Smail last updated on 02/Jan/19
![let u=tan(t/2)⇒dt=((2du)/(1+u^2 )) sint=((2u)/(1+u^2 )) f(x)=2∫_0 ^1 (du/((1+u^2 )(1+((2xu)/(1+u^2 ))))) =2∫_0 ^1 (du/(u^2 +2xu+1))=2∫_0 ^1 (du/((u+x)^2 +1−x^2 )) if −1<x≤1 f(x)=(2/(1−x^2 ))∫_0 ^1 (du/((((u+x)/(√(1−x^2 ))))^2 +1)) θ=((u+x)/(√(1−x^2 )))⇒dθ=(du/(√(1−x^2 ))) f(x)=(2/(√(1−x^2 )))∫_(x/(√(1−x^2 ))) ^((1+x)/(√(1−x^2 ))) (dθ/(θ^2 +1)) =(2/(√(1−x^2 )))[tan^(−1) (θ)]_(x/(√(1−x^2 ))) ^((1+x)/(√(1−x^2 ))) =(2/(√(1−x^2 )))(tan^(−1) (((1+x)/(√(1−x^2 ))))−tan^(−1) ((x/(√(1−x^2 )))))](Q52015.png)
$${let}\:{u}={tan}\left({t}/\mathrm{2}\right)\Rightarrow{dt}=\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $${sint}=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $${f}\left({x}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2}{xu}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$ $$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{{u}^{\mathrm{2}} +\mathrm{2}{xu}+\mathrm{1}}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\left({u}+{x}\right)^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{2}} } \\ $$ $${if}\:−\mathrm{1}<{x}\leqslant\mathrm{1} \\ $$ $${f}\left({x}\right)=\frac{\mathrm{2}}{\mathrm{1}−{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\left(\frac{{u}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$ $$\theta=\frac{{u}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\Rightarrow{d}\theta=\frac{{du}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$ $${f}\left({x}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\int_{{x}/\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} ^{\left(\mathrm{1}+{x}\right)/\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \frac{{d}\theta}{\theta^{\mathrm{2}} +\mathrm{1}} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left[{tan}^{−\mathrm{1}} \left(\theta\right)\right]_{{x}/\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} ^{\left(\mathrm{1}+{x}\right)/\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)−{tan}^{−\mathrm{1}} \left(\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\right) \\ $$