Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 52025 by Tawa1 last updated on 02/Jan/19

Commented by Abdo msup. last updated on 03/Jan/19

8)(x+1)^6 +(x−1)^6 =0 ⇔(((x−1)^6 )/((x+1)^6 )) =−1 ⇔ (((x−1)/(x+1)))^6 =−1 let ((x−1)/(x+1)) =z ⇒z^6 =−1 ⇒ z^6 =e^(i(2k+1)π) ⇒the roots of this (e) are z_k =e^(i(((2k+1)π)/6)) and k∈[[0,5]] ⇒the roots of the first (e) are x_k / ((x_k −1)/(x_k +1)) =z_k ⇒x_k −1 =z_k x_k +z_k ⇒ (1−z_k )x_k = 1+z_k ⇒x_k =((1+z_k )/(1−z_k )) =((1+cos(((2k+1)/6)π) +isin((((2k+1)π)/6)))/(1−cos((((2k+1)π)/6))−isin((((2k+1)π)/6)))) =((2cos^2 ((((2k+1)π)/(12))) +2isin((((2k+1)π)/(12)))cos((((2k+1)π)/(12))))/(2sin^2 ((((2k+1)π)/(12)))−2isin((((2k+1)π)/(12)))cos((((2k+1)π)/(12))))) =(1/(tan((((2k+1)π)/(12))))) (e^(i(((2k+1)π)/(12))) /(−i e^((i(2k+1)π)/(13)) )) =icotan((((2k+1)π)/(12))) ⇒ the roots are x_k =i cotan((((2k+1)π)/(12))) with k∈{0,1,2,3,4,5}

$$\left.\mathrm{8}\right)\left({x}+\mathrm{1}\right)^{\mathrm{6}} +\left({x}−\mathrm{1}\right)^{\mathrm{6}} =\mathrm{0}\:\Leftrightarrow\frac{\left({x}−\mathrm{1}\right)^{\mathrm{6}} }{\left({x}+\mathrm{1}\right)^{\mathrm{6}} }\:=−\mathrm{1}\:\Leftrightarrow \\ $$$$\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{6}} \:=−\mathrm{1}\:\:{let}\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\:={z}\:\Rightarrow{z}^{\mathrm{6}} =−\mathrm{1}\:\Rightarrow \\ $$$${z}^{\mathrm{6}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow{the}\:{roots}\:{of}\:{this}\:\left({e}\right)\:{are} \\ $$$${z}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{6}}} \:\:{and}\:{k}\in\left[\left[\mathrm{0},\mathrm{5}\right]\right]\:\Rightarrow{the}\:{roots}\:{of}\:{the}\:{first} \\ $$$$\left({e}\right)\:{are}\:{x}_{{k}} /\:\:\:\:\:\:\frac{{x}_{{k}} −\mathrm{1}}{{x}_{{k}} +\mathrm{1}}\:={z}_{{k}} \:\Rightarrow{x}_{{k}} −\mathrm{1}\:={z}_{{k}} {x}_{{k}} \:+{z}_{{k}} \Rightarrow \\ $$$$\left(\mathrm{1}−{z}_{{k}} \right){x}_{{k}} =\:\mathrm{1}+{z}_{{k}} \:\Rightarrow{x}_{{k}} =\frac{\mathrm{1}+{z}_{{k}} }{\mathrm{1}−{z}_{{k}} } \\ $$$$=\frac{\mathrm{1}+{cos}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{6}}\pi\right)\:+{isin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{6}}\right)}{\mathrm{1}−{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{6}}\right)−{isin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{6}}\right)} \\ $$$$=\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)\:+\mathrm{2}{isin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right){cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)−\mathrm{2}{isin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right){cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)} \\ $$$$=\frac{\mathrm{1}}{{tan}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)}\:\frac{{e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}} }{−{i}\:{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{13}}} }\:={icotan}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right) \\ $$$$\Rightarrow\:{the}\:{roots}\:{are}\:{x}_{{k}} ={i}\:{cotan}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)\:{with} \\ $$$${k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\} \\ $$

Commented by Tawa1 last updated on 03/Jan/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 03/Jan/19

Sir, what of the deduction . Thanks for your time

$$\mathrm{Sir},\:\mathrm{what}\:\mathrm{of}\:\mathrm{the}\:\mathrm{deduction}\:.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Commented by maxmathsup by imad last updated on 03/Jan/19

you are welcome sir.

$${you}\:{are}\:{welcome}\:{sir}. \\ $$

Commented by maxmathsup by imad last updated on 03/Jan/19

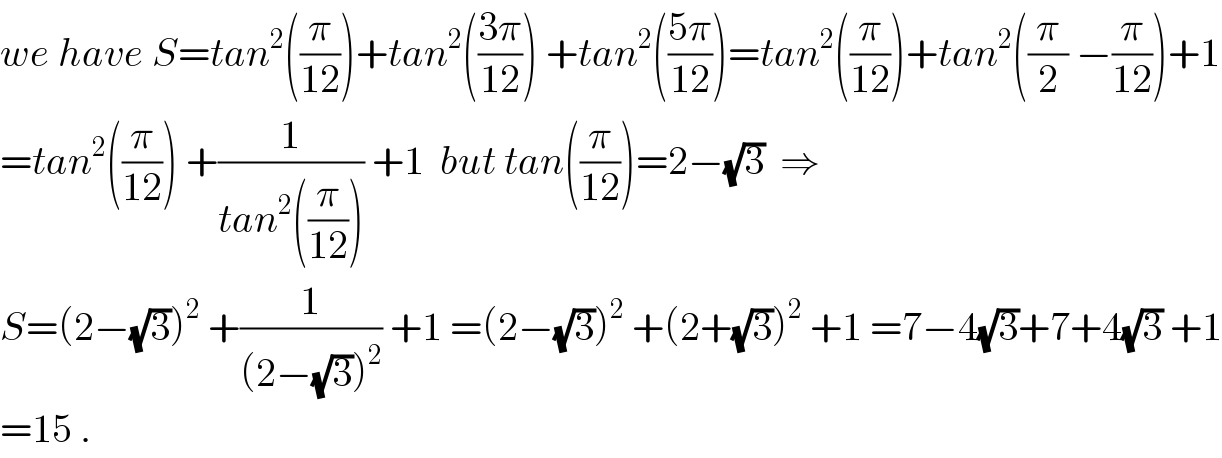
we have S=tan^2 ((π/(12)))+tan^2 (((3π)/(12))) +tan^2 (((5π)/(12)))=tan^2 ((π/(12)))+tan^2 ((π/2) −(π/(12)))+1 =tan^2 ((π/(12))) +(1/(tan^2 ((π/(12))))) +1 but tan((π/(12)))=2−(√3) ⇒ S=(2−(√3))^2 +(1/((2−(√3))^2 )) +1 =(2−(√3))^2 +(2+(√3))^2 +1 =7−4(√3)+7+4(√3) +1 =15 .

$${we}\:{have}\:{S}={tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)+{tan}^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{12}}\right)\:+{tan}^{\mathrm{2}} \left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)={tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)+{tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{12}}\right)+\mathrm{1} \\ $$$$={tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)\:+\frac{\mathrm{1}}{{tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)}\:+\mathrm{1}\:\:{but}\:{tan}\left(\frac{\pi}{\mathrm{12}}\right)=\mathrm{2}−\sqrt{\mathrm{3}}\:\:\Rightarrow \\ $$$${S}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:+\mathrm{1}\:=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:+\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:+\mathrm{1} \\ $$$$=\mathrm{15}\:. \\ $$

Commented by maxmathsup by imad last updated on 03/Jan/19

cos^2 ((π/(12)))=((1+((√3)/2))/2) =((2+(√3))/4) ⇒cos((π/(12)))=((√(2+(√3)))/2) sin((π/(12)))=((√(2−(√3)))/2) ⇒tan((π/(12)))=((√(2−(√3)))/(√(2+(√3)))) =(((√(2−(√3)))(√(2−(√3))))/(√(2^2 −3))) =2−(√3).

$${cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)=\frac{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}\:=\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{4}}\:\Rightarrow{cos}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$${sin}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:\Rightarrow{tan}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}\:=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\sqrt{\mathrm{2}^{\mathrm{2}} −\mathrm{3}}}\:=\mathrm{2}−\sqrt{\mathrm{3}}. \\ $$

Commented by Tawa1 last updated on 03/Jan/19

God bless you sir. i appreciate

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Commented by Abdo msup. last updated on 13/Jan/19

most welcome.

$${most}\:{welcome}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jan/19

7)x^9 −x^5 +x^4 −1=0 x^5 (x^4 −1)+1(x^4 −1)=0 (x^4 −1)(x^5 +1)=0 when x^4 −1=0 x^4 =1=cos2kπ+isin2kπ x=cos(((2kπ)/4))+isin(((2kπ)/4))=cos(((kπ)/2))+isin(((kπ)/2)) put k=0,1,2,3 x^5 +1=0 x^5 =−1=cosπ+isinπ=cos(2kπ+π)+isin(2kπ+π) x=cos(((2k+1)/5))π+isin(((2k+1)/5))π put n=0,1,2,3,4

$$\left.\mathrm{7}\right){x}^{\mathrm{9}} −{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{5}} \left({x}^{\mathrm{4}} −\mathrm{1}\right)+\mathrm{1}\left({x}^{\mathrm{4}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} −\mathrm{1}\right)\left({x}^{\mathrm{5}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${when}\:{x}^{\mathrm{4}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} =\mathrm{1}={cos}\mathrm{2}{k}\pi+{isin}\mathrm{2}{k}\pi \\ $$$${x}={cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{4}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{4}}\right)={cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)+{isin}\left(\frac{{k}\pi}{\mathrm{2}}\right) \\ $$$${put}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$${x}^{\mathrm{5}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{5}} =−\mathrm{1}={cos}\pi+{isin}\pi={cos}\left(\mathrm{2}{k}\pi+\pi\right)+{isin}\left(\mathrm{2}{k}\pi+\pi\right) \\ $$$${x}={cos}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{5}}\right)\pi+{isin}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{5}}\right)\pi \\ $$$${put}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4} \\ $$

Commented by Tawa1 last updated on 02/Jan/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jan/19

8)(x+1)^6 +(x−1)^6 =0 (x^6 +6c_1 x^5 +6c_2 x^4 +6c_3 x^3 +6c_4 x^2 +6c_5 x+6c_6 )+ (x^6 −6c_1 x^5 +6c_2 x^4 −6c_3 x^3 +6c_4 x^2 −6c_5 x+6c_6 )=0 adding 2(x^6 +((6×5)/2)x^4 +((6×5)/2)x^2 +1)=0 x^6 +15x^4 +15x^2 +1=0 x^3 +15x+((15)/x)+(1/x^3 )=0 (x^3 +(1/x^3 ))+15(x+(1/x))=0 (x+(1/x))^3 −3(x+(1/x))+15(x+(1/x))=0 (x+(1/x))^3 +12(x+(1/x))=0 (x+(1/x))[(x+(1/x))^2 +12]=0 when x+(1/x)=0 x^2 +1=0 x^2 =−1=cosπ+isinπ=cos(2kπ+π)+isin(2kπ+π) x=cos(((2k+1)/2))π+isin(((2k+1)/2))π put k=0 and 1 x_1 =cos(π/2)+isin(π/2)=i x_2 =cos(((3π)/2))+isin(((3π)/2))=−i (x+(1/x))^2 +12=0 x^2 +2+(1/x^2 )+12=0 x^4 +14x^2 +1=0 x^2 =((−14±(√(196−4)))/2)=((−14±(√(192)))/2)=((−14±8(√3))/2) x^2 =−7+4(√3) =−1(7−4(√3) ) x^2 =i^2 (2−(√3) )^2 x=±i(2−(√3) ) when x^2 =−7−4(√3) =−1(7+4(√3) ) x^2 =i^2 (2+(√3) )^2 x=±i(2+(√3) ) so roots are x→[ ±i ,±i(2−(√3) ),±i(2+(√3) )] alternative way to solve....i am trying...

$$\left.\mathrm{8}\right)\left({x}+\mathrm{1}\right)^{\mathrm{6}} +\left({x}−\mathrm{1}\right)^{\mathrm{6}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{6}} +\mathrm{6}{c}_{\mathrm{1}} {x}^{\mathrm{5}} +\mathrm{6}{c}_{\mathrm{2}} {x}^{\mathrm{4}} +\mathrm{6}{c}_{\mathrm{3}} {x}^{\mathrm{3}} +\mathrm{6}{c}_{\mathrm{4}} {x}^{\mathrm{2}} +\mathrm{6}{c}_{\mathrm{5}} {x}+\mathrm{6}{c}_{\mathrm{6}} \right)+ \\ $$$$\left({x}^{\mathrm{6}} −\mathrm{6}{c}_{\mathrm{1}} {x}^{\mathrm{5}} +\mathrm{6}{c}_{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{6}{c}_{\mathrm{3}} {x}^{\mathrm{3}} +\mathrm{6}{c}_{\mathrm{4}} {x}^{\mathrm{2}} −\mathrm{6}{c}_{\mathrm{5}} {x}+\mathrm{6}{c}_{\mathrm{6}} \right)=\mathrm{0} \\ $$$${adding} \\ $$$$\mathrm{2}\left({x}^{\mathrm{6}} +\frac{\mathrm{6}×\mathrm{5}}{\mathrm{2}}{x}^{\mathrm{4}} +\frac{\mathrm{6}×\mathrm{5}}{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{6}} +\mathrm{15}{x}^{\mathrm{4}} +\mathrm{15}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +\mathrm{15}{x}+\frac{\mathrm{15}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)+\mathrm{15}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} −\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{15}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} +\mathrm{12}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left[\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{12}\right]=\mathrm{0} \\ $$$${when}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =−\mathrm{1}={cos}\pi+{isin}\pi={cos}\left(\mathrm{2}{k}\pi+\pi\right)+{isin}\left(\mathrm{2}{k}\pi+\pi\right) \\ $$$${x}={cos}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}\right)\pi+{isin}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}\right)\pi \\ $$$${put}\:{k}=\mathrm{0}\:{and}\:\mathrm{1} \\ $$$${x}_{\mathrm{1}} ={cos}\frac{\pi}{\mathrm{2}}+{isin}\frac{\pi}{\mathrm{2}}={i} \\ $$$${x}_{\mathrm{2}} ={cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)+{isin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)=−{i} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{12}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{12}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{14}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{−\mathrm{14}\pm\sqrt{\mathrm{196}−\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{14}\pm\sqrt{\mathrm{192}}}{\mathrm{2}}=\frac{−\mathrm{14}\pm\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =−\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:=−\mathrm{1}\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\:\right) \\ $$$${x}^{\mathrm{2}} ={i}^{\mathrm{2}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \:\:{x}=\pm{i}\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right) \\ $$$${when}\:{x}^{\mathrm{2}} =−\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\:=−\mathrm{1}\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:\right) \\ $$$${x}^{\mathrm{2}} ={i}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \\ $$$${x}=\pm{i}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right) \\ $$$${so}\:{roots}\:{are}\:{x}\rightarrow\left[\:\pm{i}\:,\pm{i}\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right),\pm{i}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)\right] \\ $$$$\boldsymbol{{alternative}}\:\boldsymbol{{way}}\:\boldsymbol{{to}}\:\boldsymbol{{solve}}....{i}\:{am}\:{trying}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Tawa1 last updated on 02/Jan/19

God bless you sir. Thanks for your time sir. i appreciate

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jan/19

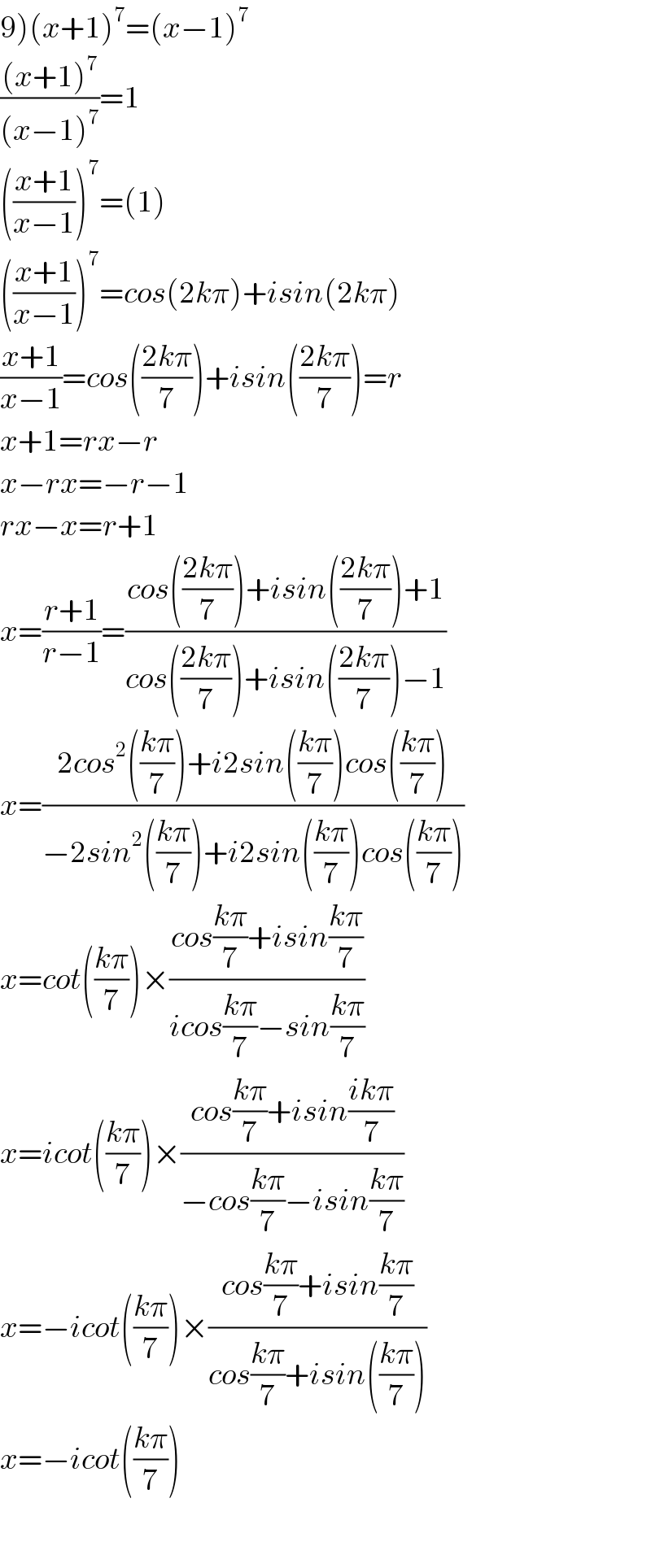
9)(x+1)^7 =(x−1)^7 (((x+1)^7 )/((x−1)^7 ))=1 (((x+1)/(x−1)))^7 =(1) (((x+1)/(x−1)))^7 =cos(2kπ)+isin(2kπ) ((x+1)/(x−1))=cos(((2kπ)/7))+isin(((2kπ)/7))=r x+1=rx−r x−rx=−r−1 rx−x=r+1 x=((r+1)/(r−1))=((cos(((2kπ)/7))+isin(((2kπ)/7))+1)/(cos(((2kπ)/7))+isin(((2kπ)/7))−1)) x=((2cos^2 (((kπ)/7))+i2sin(((kπ)/7))cos(((kπ)/7)))/(−2sin^2 (((kπ)/7))+i2sin(((kπ)/7))cos(((kπ)/7)))) x=cot(((kπ)/7))×((cos((kπ)/7)+isin((kπ)/7))/(icos((kπ)/7)−sin((kπ)/7))) x=icot(((kπ)/7))×((cos((kπ)/7)+isin((ikπ)/7))/(−cos((kπ)/7)−isin((kπ)/7))) x=−icot(((kπ)/7))×((cos((kπ)/7)+isin((kπ)/7))/(cos((kπ)/7)+isin(((kπ)/7)))) x=−icot(((kπ)/7))

$$\left.\mathrm{9}\right)\left({x}+\mathrm{1}\right)^{\mathrm{7}} =\left({x}−\mathrm{1}\right)^{\mathrm{7}} \\ $$$$\frac{\left({x}+\mathrm{1}\right)^{\mathrm{7}} }{\left({x}−\mathrm{1}\right)^{\mathrm{7}} }=\mathrm{1} \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{7}} =\left(\mathrm{1}\right) \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{7}} ={cos}\left(\mathrm{2}{k}\pi\right)+{isin}\left(\mathrm{2}{k}\pi\right) \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}={cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)={r} \\ $$$${x}+\mathrm{1}={rx}−{r} \\ $$$${x}−{rx}=−{r}−\mathrm{1} \\ $$$${rx}−{x}={r}+\mathrm{1} \\ $$$${x}=\frac{{r}+\mathrm{1}}{{r}−\mathrm{1}}=\frac{{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)+\mathrm{1}}{{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)−\mathrm{1}} \\ $$$${x}=\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{7}}\right)+{i}\mathrm{2}{sin}\left(\frac{{k}\pi}{\mathrm{7}}\right){cos}\left(\frac{{k}\pi}{\mathrm{7}}\right)}{−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{7}}\right)+{i}\mathrm{2}{sin}\left(\frac{{k}\pi}{\mathrm{7}}\right){cos}\left(\frac{{k}\pi}{\mathrm{7}}\right)} \\ $$$${x}={cot}\left(\frac{{k}\pi}{\mathrm{7}}\right)×\frac{{cos}\frac{{k}\pi}{\mathrm{7}}+{isin}\frac{{k}\pi}{\mathrm{7}}}{{icos}\frac{{k}\pi}{\mathrm{7}}−{sin}\frac{{k}\pi}{\mathrm{7}}} \\ $$$${x}={icot}\left(\frac{{k}\pi}{\mathrm{7}}\right)×\frac{{cos}\frac{{k}\pi}{\mathrm{7}}+{isin}\frac{{ik}\pi}{\mathrm{7}}}{−{cos}\frac{{k}\pi}{\mathrm{7}}−{isin}\frac{{k}\pi}{\mathrm{7}}} \\ $$$${x}=−{icot}\left(\frac{{k}\pi}{\mathrm{7}}\right)×\frac{{cos}\frac{{k}\pi}{\mathrm{7}}+{isin}\frac{{k}\pi}{\mathrm{7}}}{{cos}\frac{{k}\pi}{\mathrm{7}}+{isin}\left(\frac{{k}\pi}{\mathrm{7}}\right)} \\ $$$${x}=−{icot}\left(\frac{{k}\pi}{\mathrm{7}}\right) \\ $$$$ \\ $$

Commented by Tawa1 last updated on 02/Jan/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jan/19

8)alternative.. (x+1)^6 +(x−1)^6 =0 (((x+1)/(x−1)))^6 +1=0 (((x+1)/(x−1)))^6 =−1=cos(2kπ+π)+isin(2kπ+π) (((x+1)/(x−1)))=cos(((2kπ+π)/6))+isin(((2kπ+π)/6)) ((x+1)/(x−1))=r x+1=rx−r x−rx=−r−1 rx−x=r+1 x=((r+1)/(r−1))=((1+(1/r))/(1−(1/r)))=((1+cos(((2kπ+π)/6))−isin(((2kπ+π)/6)))/(1−cos(((2kπ+π)/6))+isin(((2kπ+π)/6)))) x=((2cos^2 (((2kπ+π)/(12)))−2isin(((2kπ+π)/(12)))cos(((2kπ+π)/(12))))/(2sin^2 (((2kπ+π)/(12)))+2icos(((2kπ+π)/(12)))sin(((2kπ+π)/(12))))) x=cot(((2kπ+π)/(12)))×((cos(((2kπ+π)/(12)))−isin(((2kπ+π)/(12))))/(sin(((2kπ+π)/(12)))+icos(((2kπ+π)/(12))))) x=icot(((2kπ+π)/(12)))×((cos(((2kπ+π)/(12)))−isin(((2kπ+π)/(12))))/(−cos(((2kπ+π)/(12)))+isin(((2kπ+π)/(12))))) x=−icot(((2kπ+π)/(12)))

$$\left.\mathrm{8}\right){alternative}.. \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{6}} +\left({x}−\mathrm{1}\right)^{\mathrm{6}} =\mathrm{0} \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{6}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{6}} =−\mathrm{1}={cos}\left(\mathrm{2}{k}\pi+\pi\right)+{isin}\left(\mathrm{2}{k}\pi+\pi\right) \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)={cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right) \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}={r} \\ $$$${x}+\mathrm{1}={rx}−{r} \\ $$$${x}−{rx}=−{r}−\mathrm{1} \\ $$$${rx}−{x}={r}+\mathrm{1} \\ $$$${x}=\frac{{r}+\mathrm{1}}{{r}−\mathrm{1}}=\frac{\mathrm{1}+\frac{\mathrm{1}}{{r}}}{\mathrm{1}−\frac{\mathrm{1}}{{r}}}=\frac{\mathrm{1}+{cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right)}{\mathrm{1}−{cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{6}}\right)} \\ $$$${x}=\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)−\mathrm{2}{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right){cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)+\mathrm{2}{icos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right){sin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)} \\ $$$${x}={cot}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)×\frac{{cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)}{{sin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)+{icos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)} \\ $$$${x}={icot}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)×\frac{{cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)}{−{cos}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right)} \\ $$$${x}=−{icot}\left(\frac{\mathrm{2}{k}\pi+\pi}{\mathrm{12}}\right) \\ $$

Commented by Tawa1 last updated on 03/Jan/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 03/Jan/19

Sir, what of the deduction sir. Thanks for your time sir.

$$\mathrm{Sir},\:\mathrm{what}\:\mathrm{of}\:\mathrm{the}\:\mathrm{deduction}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com