Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 52086 by prakash jain last updated on 03/Jan/19

If 1,a_(1,) a_2 ,...,a_(n−1) are n^(th) roots of unity, then prove that. (1+a_1 )(1+a_2 )..(1+a_(n−1) )= n if n is even 0 if n is odd

$$\mathrm{If}\:\mathrm{1},{a}_{\mathrm{1},} {a}_{\mathrm{2}} ,...,{a}_{{n}−\mathrm{1}} \:\mathrm{are}\:{n}^{{th}} \:\mathrm{roots}\:\mathrm{of} \\ $$$$\mathrm{unity},\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}. \\ $$$$\left(\mathrm{1}+{a}_{\mathrm{1}} \right)\left(\mathrm{1}+{a}_{\mathrm{2}} \right)..\left(\mathrm{1}+{a}_{{n}−\mathrm{1}} \right)= \\ $$$${n}\:\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{0}\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{odd} \\ $$

Commented by mr W last updated on 03/Jan/19

should it be =n if n is odd =0 if n is even?

$${should}\:{it}\:{be}\: \\ $$$$={n}\:{if}\:{n}\:{is}\:{odd} \\ $$$$=\mathrm{0}\:{if}\:{n}\:{is}\:{even}? \\ $$

Commented by mr W last updated on 03/Jan/19

please check the question sir: n=3: a_1 =ω=−(1/2)+((√3)/2)i a_2 =ω^2 =−(1/2)−((√3)/2) (1+a_1 )(1+a_2 )=((1/2)−((√3)/2)i)((1/2)+((√3)/2)i) =(1/4)+(3/4) =1≠n=3

$${please}\:{check}\:{the}\:{question}\:{sir}: \\ $$$${n}=\mathrm{3}: \\ $$$${a}_{\mathrm{1}} =\omega=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$$${a}_{\mathrm{2}} =\omega^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{a}_{\mathrm{1}} \right)\left(\mathrm{1}+{a}_{\mathrm{2}} \right)=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\mathrm{1}\neq{n}=\mathrm{3} \\ $$

Commented by prakash jain last updated on 03/Jan/19

You are correct. The question should 1 for n odd. And 0 for n even

Answered by mr W last updated on 04/Jan/19

see question above a_k =cos ((2kπ)/n)+i sin ((2kπ)/n), k=0,1,2,...,n−1 1+a_k =1+cos ((2kπ)/n)+i sin ((2kπ)/n) 1+a_k =2cos^2 ((kπ)/n)+i 2sin ((kπ)/n)cos ((kπ)/n) 1+a_k =2cos ((kπ)/n)(cos ((kπ)/n)+i sin ((kπ)/n)) P=Π_(k=1) ^(n−1) (1+a_k )=2^(n−1) Π_(k=1) ^(n−1) cos ((kπ)/n) Π_(k=1) ^(n−1) (cos ((kπ)/n)+i sin ((kπ)/n)) if n=even: at k=(n/2): cos ((kπ)/n)=cos (π/2)=0 ⇒P=0 if n=odd: cos (((n−1)π)/n)=cos (π−(π/n))=−cos (π/n) sin (((n−1)π)/n)=sin (π−(π/n))=sin (π/n) [cos (((n−1)π)/n)+i sin (((n−1)π)/n)][cos (π/n)+i sin (π/n)] =[−cos (π/n)+i sin (π/n)][cos (π/n)+i sin (π/n)] =−[cos (π/n)−i sin (π/n)][cos (π/n)+i sin (π/n)] =−[cos^2 (π/n)+sin^2 (π/n)] =−1 ⇒Π_(k=1) ^(n−1) (cos ((kπ)/n)+i sin ((kπ)/n))=(−1)^((n−1)/2) =1 cos (π/n) cos (((n−1)π)/n)=−cos^2 (π/n) cos ((2π)/n) cos (((n−2)π)/n)=−cos^2 ((2π)/n) P=2^(n−1) cos^2 (π/n) cos^2 ((2π)/n) cos^2 ((3π)/n) ... cos^2 (((n−1)π)/(2n)) P=2^(n−1) [cos (π/n) cos ((2π)/n) cos ((3π)/n) ... cos (((n−1)π)/(2n))]^2 ......????

$${see}\:{question}\:{above} \\ $$$${a}_{{k}} =\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{{n}},\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},...,{n}−\mathrm{1} \\ $$$$\mathrm{1}+{a}_{{k}} =\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{{n}} \\ $$$$\mathrm{1}+{a}_{{k}} =\mathrm{2cos}^{\mathrm{2}} \:\frac{{k}\pi}{{n}}+{i}\:\mathrm{2sin}\:\frac{{k}\pi}{{n}}\mathrm{cos}\:\frac{{k}\pi}{{n}} \\ $$$$\mathrm{1}+{a}_{{k}} =\mathrm{2cos}\:\frac{{k}\pi}{{n}}\left(\mathrm{cos}\:\frac{{k}\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{{k}\pi}{{n}}\right) \\ $$$${P}=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}+{a}_{{k}} \right)=\mathrm{2}^{{n}−\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\mathrm{cos}\:\frac{{k}\pi}{{n}}\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{cos}\:\frac{{k}\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{{k}\pi}{{n}}\right) \\ $$$$ \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{n}}=\boldsymbol{{even}}: \\ $$$${at}\:{k}=\frac{{n}}{\mathrm{2}}: \\ $$$$\mathrm{cos}\:\frac{{k}\pi}{{n}}=\mathrm{cos}\:\frac{\pi}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{P}=\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{n}}=\boldsymbol{{odd}}: \\ $$$$\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}=\mathrm{cos}\:\left(\pi−\frac{\pi}{{n}}\right)=−\mathrm{cos}\:\frac{\pi}{{n}} \\ $$$$\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}=\mathrm{sin}\:\left(\pi−\frac{\pi}{{n}}\right)=\mathrm{sin}\:\frac{\pi}{{n}} \\ $$$$\left[\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right]\left[\mathrm{cos}\:\frac{\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\pi}{{n}}\right] \\ $$$$=\left[−\mathrm{cos}\:\frac{\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\pi}{{n}}\right]\left[\mathrm{cos}\:\frac{\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\pi}{{n}}\right] \\ $$$$=−\left[\mathrm{cos}\:\frac{\pi}{{n}}−{i}\:\mathrm{sin}\:\frac{\pi}{{n}}\right]\left[\mathrm{cos}\:\frac{\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{\pi}{{n}}\right] \\ $$$$=−\left[\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{{n}}+\mathrm{sin}^{\mathrm{2}} \:\frac{\pi}{{n}}\right] \\ $$$$=−\mathrm{1} \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{cos}\:\frac{{k}\pi}{{n}}+{i}\:\mathrm{sin}\:\frac{{k}\pi}{{n}}\right)=\left(−\mathrm{1}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} =\mathrm{1} \\ $$$$ \\ $$$$\mathrm{cos}\:\frac{\pi}{{n}}\:\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}=−\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{{n}} \\ $$$$\mathrm{cos}\:\frac{\mathrm{2}\pi}{{n}}\:\mathrm{cos}\:\frac{\left({n}−\mathrm{2}\right)\pi}{{n}}=−\mathrm{cos}^{\mathrm{2}} \:\frac{\mathrm{2}\pi}{{n}} \\ $$$${P}=\mathrm{2}^{{n}−\mathrm{1}} \:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{{n}}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\mathrm{2}\pi}{{n}}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{{n}}\:...\:\mathrm{cos}^{\mathrm{2}} \:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}} \\ $$$${P}=\mathrm{2}^{{n}−\mathrm{1}} \left[\mathrm{cos}\:\frac{\pi}{{n}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{{n}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{{n}}\:...\:\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}\right]^{\mathrm{2}} \\ $$$$......???? \\ $$

Commented by prakash jain last updated on 03/Jan/19

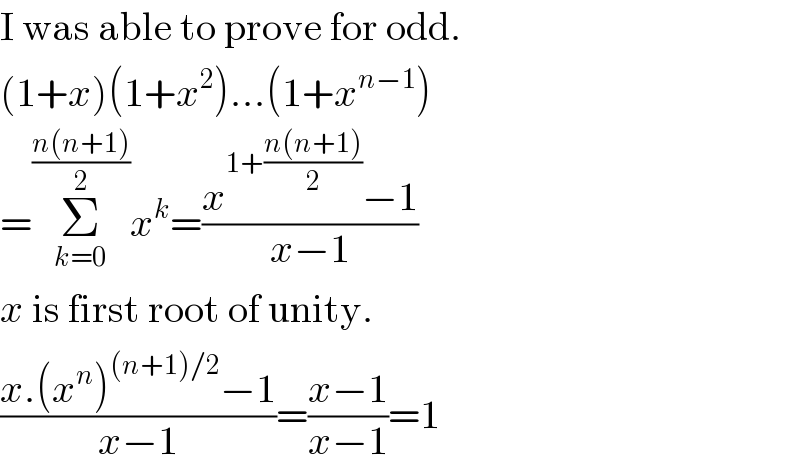
I was able to prove for odd. (1+x)(1+x^2 )...(1+x^(n−1) ) =Σ_(k=0) ^((n(n+1))/2) x^k =((x^(1+((n(n+1))/2)) −1)/(x−1)) x is first root of unity. ((x.(x^n )^((n+1)/2) −1)/(x−1))=((x−1)/(x−1))=1

$$\mathrm{I}\:\mathrm{was}\:\mathrm{able}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{for}\:\mathrm{odd}. \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)...\left(\mathrm{1}+{x}^{{n}−\mathrm{1}} \right) \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} {\sum}}{x}^{{k}} =\frac{{x}^{\mathrm{1}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$${x}\:\mathrm{is}\:\mathrm{first}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\frac{{x}.\left({x}^{{n}} \right)^{\left({n}+\mathrm{1}\right)/\mathrm{2}} −\mathrm{1}}{{x}−\mathrm{1}}=\frac{{x}−\mathrm{1}}{{x}−\mathrm{1}}=\mathrm{1} \\ $$

Commented by mr W last updated on 03/Jan/19

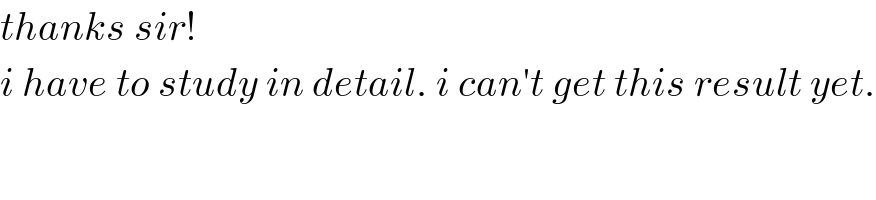
thanks sir! i have to study in detail. i can′t get this result yet.

$${thanks}\:{sir}! \\ $$$${i}\:{have}\:{to}\:{study}\:{in}\:{detail}.\:{i}\:{can}'{t}\:{get}\:{this}\:{result}\:{yet}. \\ $$

Commented by mr W last updated on 04/Jan/19

I studied your workings and unterstand now. should the third line not be =Σ_(k=0) ^((n(n−1))/2) x^k =((x^(1+((n(n−1))/2)) −1)/(x−1)) ? why must n be odd? i can′t see this restriction in your workings.

$${I}\:{studied}\:{your}\:{workings}\:{and}\:{unterstand} \\ $$$${now}. \\ $$$${should}\:{the}\:{third}\:{line}\:{not}\:{be} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}} {\sum}}{x}^{{k}} =\frac{{x}^{\mathrm{1}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}} −\mathrm{1}}{{x}−\mathrm{1}}\:? \\ $$$${why}\:{must}\:{n}\:{be}\:{odd}?\:{i}\:{can}'{t}\:{see}\:{this} \\ $$$${restriction}\:{in}\:{your}\:{workings}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com