Question Number 52129 by ajfour last updated on 03/Jan/19
Commented by ajfour last updated on 03/Jan/19
$${Find}\:{radius}\:\boldsymbol{{r}}\:{of}\:{circles}\:\left({the}\:{same}\right) \\ $$$${in}\:{terms}\:{of}\:{square}\:{side}\:\boldsymbol{{a}}. \\ $$
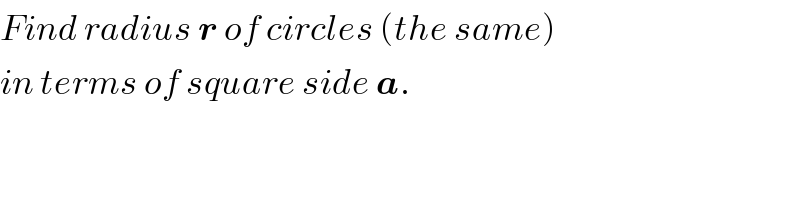
Commented by ajfour last updated on 03/Jan/19
![r(√2)+r+b = a(√2) ....(i) AP^2 = b^2 +(r+r(√2))^2 ...(ii) also AP = (a−r)+(a−r−CP) ⇒ AP = a−r+a−r−(√2)(r+r(√2)) AP = 2a−r(4+(√2)) ...(iii) ⇒ [2a−r(4+(√2))]^2 =[a(√2)−r(1+(√2))]^2 +(r+r(√2))^2 ⇒ 4a^2 −4ar(4+(√2))+(18+8(√2))r^2 = 2a^2 −2ar(2+(√2))+(6+4(√2))r^2 ⇒ 2a^2 −ar(12+2(√2))+(12+4(√2))r^2 = 0 ⇒ (6+2(√2))r^2 −(6+(√2))ar+a^2 = 0 let (r/a) = λ ⇒ (6+2(√2))λ^2 −(6+(√2))λ+1 = 0 λ ≈ 0.1688a (& 0.671a not acceptable).](Q52151.png)
$${r}\sqrt{\mathrm{2}}+{r}+{b}\:=\:{a}\sqrt{\mathrm{2}}\:\:\:\:....\left({i}\right) \\ $$$${AP}\:^{\mathrm{2}} =\:{b}^{\mathrm{2}} +\left({r}+{r}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$${also}\:\:\:\:{AP}\:=\:\left({a}−{r}\right)+\left({a}−{r}−{CP}\right) \\ $$$$\Rightarrow\:\:\:{AP}\:=\:{a}−{r}+{a}−{r}−\sqrt{\mathrm{2}}\left({r}+{r}\sqrt{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:{AP}\:\:=\:\mathrm{2}{a}−{r}\left(\mathrm{4}+\sqrt{\mathrm{2}}\right)\:\:\:\:...\left({iii}\right) \\ $$$$\Rightarrow\:\:\:\left[\mathrm{2}{a}−{r}\left(\mathrm{4}+\sqrt{\mathrm{2}}\right)\right]^{\mathrm{2}} =\left[{a}\sqrt{\mathrm{2}}−{r}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({r}+{r}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ar}\left(\mathrm{4}+\sqrt{\mathrm{2}}\right)+\left(\mathrm{18}+\mathrm{8}\sqrt{\mathrm{2}}\right){r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ar}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right){r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}{a}^{\mathrm{2}} −{ar}\left(\mathrm{12}+\mathrm{2}\sqrt{\mathrm{2}}\right)+\left(\mathrm{12}+\mathrm{4}\sqrt{\mathrm{2}}\right){r}^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{2}}\right){r}^{\mathrm{2}} −\left(\mathrm{6}+\sqrt{\mathrm{2}}\right){ar}+{a}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\:{let}\:\:\frac{{r}}{{a}}\:=\:\lambda \\ $$$$\Rightarrow\:\:\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{2}}\right)\lambda^{\mathrm{2}} −\left(\mathrm{6}+\sqrt{\mathrm{2}}\right)\lambda+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\lambda\:\approx\:\mathrm{0}.\mathrm{1688}{a}\:\:\:\:\left(\&\:\mathrm{0}.\mathrm{671}{a}\:\:{not}\:{acceptable}\right). \\ $$
Commented by ajfour last updated on 03/Jan/19
Commented by mr W last updated on 03/Jan/19
$${good}\:{solution}! \\ $$
Commented by Olalekan99 last updated on 04/Jan/19
$${pls}\:{wat}\:{app}\: \\ $$$${did}\:{u}\:{use}\:{for}\:{the}\:{drawing} \\ $$
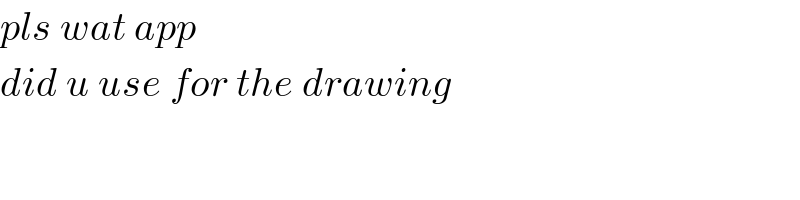
Answered by mr W last updated on 03/Jan/19
![((ax)/2)=(r/2)(a+x+(√(a^2 +x^2 ))) ⇒r=((ax)/((a+x+(√(a^2 +x^2 ))))) ...(i) (((a−x)^2 )/2)=(r/2)[2(a−x)+(√2)(a−x)] ⇒r=((a−x)/(2+(√2))) ...(ii) ((ax)/((a+x+(√(a^2 +x^2 )))))=((a−x)/(2+(√2))) let λ=(x/a) (λ/((1+λ+(√(1+λ^2 )))))=((1−λ)/(2+(√2))) λ^2 +(2+(√2))λ−1=(1−λ)(√(1+λ^2 )) ⇒(3+(√2))λ^2 +(1+2(√2))λ−(1+(√2))=0 λ=(((√((1+2(√2))^2 +4(3+(√2))(1+(√2))))−(1+2(√2)))/(2(3+(√2)))) λ=(((√(79+46(√2)))−5(√2)+1)/(14))≈0.4237 ⇒(r/a)=((1−λ)/(2+(√2)))=(1/(2+(√2)))(((13+5(√2)−(√(79+46(√2))))/(14))) ⇒(r/a)=((16−3(√2)−(√(2(53−20(√2)))))/(28))≈0.1688](Q52149.png)
$$\frac{{ax}}{\mathrm{2}}=\frac{{r}}{\mathrm{2}}\left({a}+{x}+\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{r}=\frac{{ax}}{\left({a}+{x}+\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right)}\:\:\:\:\:...\left({i}\right) \\ $$$$\frac{\left({a}−{x}\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{{r}}{\mathrm{2}}\left[\mathrm{2}\left({a}−{x}\right)+\sqrt{\mathrm{2}}\left({a}−{x}\right)\right] \\ $$$$\Rightarrow{r}=\frac{{a}−{x}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:\:\:\:\:...\left({ii}\right) \\ $$$$\frac{{ax}}{\left({a}+{x}+\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right)}=\frac{{a}−{x}}{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$${let}\:\lambda=\frac{{x}}{{a}} \\ $$$$\frac{\lambda}{\left(\mathrm{1}+\lambda+\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\right)}=\frac{\mathrm{1}−\lambda}{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$$\lambda^{\mathrm{2}} +\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\lambda−\mathrm{1}=\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)\lambda^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\right)\lambda−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\lambda=\frac{\sqrt{\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{4}\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}−\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)} \\ $$$$\lambda=\frac{\sqrt{\mathrm{79}+\mathrm{46}\sqrt{\mathrm{2}}}−\mathrm{5}\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{14}}\approx\mathrm{0}.\mathrm{4237} \\ $$$$\Rightarrow\frac{{r}}{{a}}=\frac{\mathrm{1}−\lambda}{\mathrm{2}+\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}\left(\frac{\mathrm{13}+\mathrm{5}\sqrt{\mathrm{2}}−\sqrt{\mathrm{79}+\mathrm{46}\sqrt{\mathrm{2}}}}{\mathrm{14}}\right) \\ $$$$\Rightarrow\frac{{r}}{{a}}=\frac{\mathrm{16}−\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}\left(\mathrm{53}−\mathrm{20}\sqrt{\mathrm{2}}\right)}}{\mathrm{28}}\approx\mathrm{0}.\mathrm{1688} \\ $$
Commented by ajfour last updated on 03/Jan/19
$${Thank}\:{you}\:{Sir}!\:\left({got}\:{the}\:{same}\:{finally}\right) \\ $$$$\:{and}\:{whats}\:{x}\:{in}\:{your}\:{solution}. \\ $$
Commented by mr W last updated on 03/Jan/19
$${x}\:{is}\:{BP}\:{in}\:{your}\:{diagram}. \\ $$