Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 5226 by sanusihammed last updated on 02/May/16

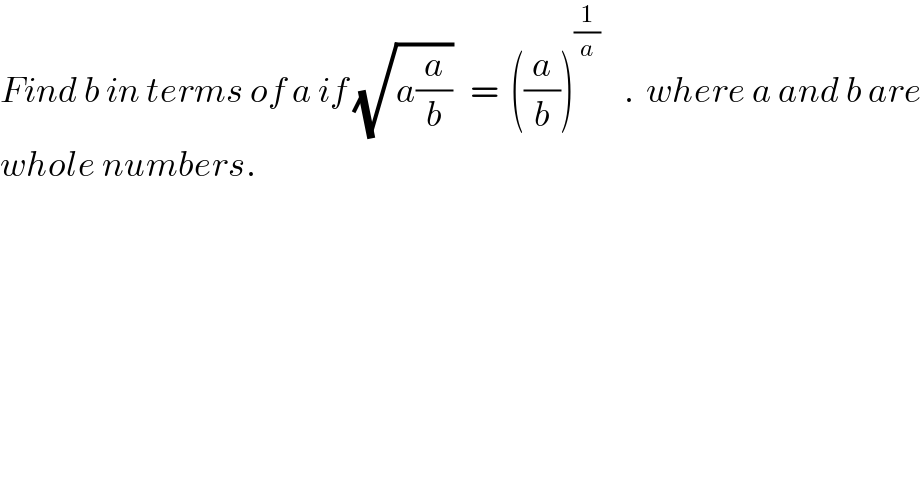
Find b in terms of a if (√(a(a/b))) = ((a/b))^(1/a) . where a and b are whole numbers.

$${Find}\:{b}\:{in}\:{terms}\:{of}\:{a}\:{if}\:\sqrt{{a}\frac{{a}}{{b}}}\:\:\:=\:\:\left(\frac{{a}}{{b}}\right)^{\frac{\mathrm{1}}{{a}}} \:\:\:\:.\:\:{where}\:{a}\:{and}\:{b}\:{are} \\ $$$${whole}\:{numbers}.\:\: \\ $$

Commented by prakash jain last updated on 02/May/16

(((ab+a)/b))^(1/2) =((a/b))^(1/a) (((ab+a)/b))^a =(a^2 /b^2 ) (((ab+a)^a )/a^2 )=(b^a /b^2 ) a^(a−2) (b+1)^a =b^(a−2) Assume we are only dealing when both LHS and RHS are real⇒(a^2 /b)>0⇒b>0 also a≠0 and b≠0 case a>0 (b+1)^a =((b/a))^(a−2) LHS is a +ve interger so RHS must be +ve integer continue

$$\left(\frac{{ab}+{a}}{{b}}\right)^{\mathrm{1}/\mathrm{2}} =\left(\frac{{a}}{{b}}\right)^{\mathrm{1}/{a}} \\ $$$$\left(\frac{{ab}+{a}}{{b}}\right)^{{a}} =\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\frac{\left({ab}+{a}\right)^{{a}} }{{a}^{\mathrm{2}} }=\frac{{b}^{{a}} }{{b}^{\mathrm{2}} } \\ $$$${a}^{{a}−\mathrm{2}} \left({b}+\mathrm{1}\right)^{{a}} ={b}^{{a}−\mathrm{2}} \\ $$$$\mathrm{Assume}\:\mathrm{we}\:\mathrm{are}\:\mathrm{only}\:\mathrm{dealing}\:\mathrm{when}\:\mathrm{both} \\ $$$$\mathrm{LHS}\:\mathrm{and}\:\mathrm{RHS}\:\mathrm{are}\:\mathrm{real}\Rightarrow\frac{{a}^{\mathrm{2}} }{{b}}>\mathrm{0}\Rightarrow{b}>\mathrm{0} \\ $$$$\mathrm{also}\:{a}\neq\mathrm{0}\:\mathrm{and}\:{b}\neq\mathrm{0} \\ $$$${case}\:{a}>\mathrm{0} \\ $$$$\left({b}+\mathrm{1}\right)^{{a}} =\left(\frac{{b}}{{a}}\right)^{{a}−\mathrm{2}} \\ $$$$\mathrm{LHS}\:\mathrm{is}\:\mathrm{a}\:+\mathrm{ve}\:\mathrm{interger}\:\mathrm{so}\:\mathrm{RHS}\:\mathrm{must}\:\mathrm{be}\:+\mathrm{ve}\:\mathrm{integer} \\ $$$${continue} \\ $$

Answered by Yozzii last updated on 02/May/16

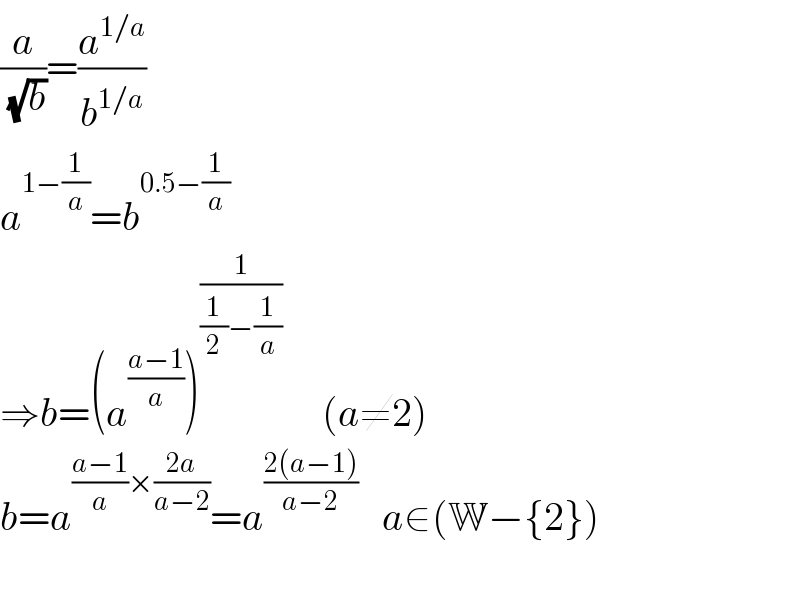
(a/(√b))=(a^(1/a) /b^(1/a) ) a^(1−(1/a)) =b^(0.5−(1/a)) ⇒b=(a^((a−1)/a) )^(1/((1/2)−(1/a))) (a≠2) b=a^(((a−1)/a)×((2a)/(a−2))) =a^((2(a−1))/(a−2)) a∈(W−{2})

$$\frac{{a}}{\sqrt{{b}}}=\frac{{a}^{\mathrm{1}/{a}} }{{b}^{\mathrm{1}/{a}} } \\ $$$${a}^{\mathrm{1}−\frac{\mathrm{1}}{{a}}} ={b}^{\mathrm{0}.\mathrm{5}−\frac{\mathrm{1}}{{a}}} \\ $$$$\Rightarrow{b}=\left({a}^{\frac{{a}−\mathrm{1}}{{a}}} \right)^{\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{a}}}} \:\:\:\:\:\left({a}\neq\mathrm{2}\right) \\ $$$${b}={a}^{\frac{{a}−\mathrm{1}}{{a}}×\frac{\mathrm{2}{a}}{{a}−\mathrm{2}}} ={a}^{\frac{\mathrm{2}\left({a}−\mathrm{1}\right)}{{a}−\mathrm{2}}} \:\:\:{a}\in\left(\mathbb{W}−\left\{\mathrm{2}\right\}\right) \\ $$$$ \\ $$

Commented by FilupSmith last updated on 02/May/16

What is W?

$$\mathrm{What}\:\mathrm{is}\:\mathbb{W}? \\ $$

Commented by sanusihammed last updated on 02/May/16

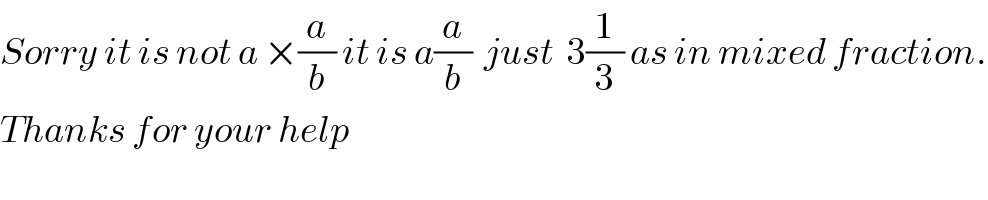
Sorry it is not a ×(a/b) it is a(a/b) just 3(1/3) as in mixed fraction. Thanks for your help

$${Sorry}\:{it}\:{is}\:{not}\:{a}\:×\frac{{a}}{{b}}\:{it}\:{is}\:{a}\frac{{a}}{{b}}\:\:{just}\:\:\mathrm{3}\frac{\mathrm{1}}{\mathrm{3}}\:{as}\:{in}\:{mixed}\:{fraction}. \\ $$$${Thanks}\:{for}\:{your}\:{help} \\ $$

Commented by Yozzii last updated on 02/May/16

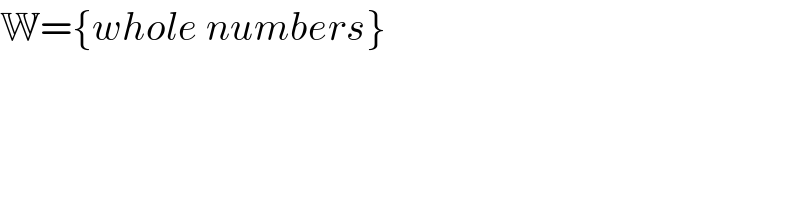
W={whole numbers}

$$\mathbb{W}=\left\{{whole}\:{numbers}\right\} \\ $$

Commented by FilupSmith last updated on 02/May/16

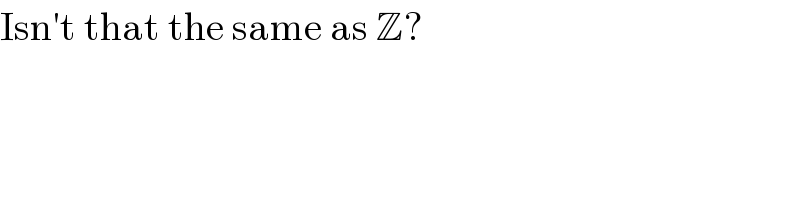
Isn′t that the same as Z?

$$\mathrm{Isn}'\mathrm{t}\:\mathrm{that}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathbb{Z}? \\ $$

Commented by Yozzii last updated on 02/May/16

Answered by Yozzii last updated on 02/May/16

(√(a+(a/b)))=(a^(1/a) /b^(1/a) ) a,b∈{whole numbers} a(1+(1/b))=(a^(2/a) /b^(2/a) ) a^a (1+(1/b))^a =a^2 /b^2 Let u=1/b a^a (1+u)^a =a^2 u^2 Let l=1+u ⇒l^a =a^(2−a) (l−1)^2 l^a =a^(2−a) (l^2 −2l+1) l^a −a^(2−a) l^2 +2a^(2−a) l−a^(2−a) =0 (∗) For a being a whole number, if a≥5 then no general algebraic solution exists for (∗), according to the Abel−Ruffini theorem.

$$\sqrt{{a}+\frac{{a}}{{b}}}=\frac{{a}^{\mathrm{1}/{a}} }{{b}^{\mathrm{1}/{a}} }\:\:\:\:\:\:\:{a},{b}\in\left\{{whole}\:{numbers}\right\} \\ $$$${a}\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)=\frac{{a}^{\mathrm{2}/{a}} }{{b}^{\mathrm{2}/{a}} } \\ $$$${a}^{{a}} \left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)^{{a}} ={a}^{\mathrm{2}} /{b}^{\mathrm{2}} \\ $$$${Let}\:{u}=\mathrm{1}/{b} \\ $$$${a}^{{a}} \left(\mathrm{1}+{u}\right)^{{a}} ={a}^{\mathrm{2}} {u}^{\mathrm{2}} \\ $$$${Let}\:{l}=\mathrm{1}+{u} \\ $$$$\Rightarrow{l}^{{a}} ={a}^{\mathrm{2}−{a}} \left({l}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${l}^{{a}} ={a}^{\mathrm{2}−{a}} \left({l}^{\mathrm{2}} −\mathrm{2}{l}+\mathrm{1}\right) \\ $$$${l}^{{a}} −{a}^{\mathrm{2}−{a}} {l}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}−{a}} {l}−{a}^{\mathrm{2}−{a}} =\mathrm{0}\:\left(\ast\right) \\ $$$${For}\:{a}\:{being}\:{a}\:{whole}\:{number},\:{if}\: \\ $$$${a}\geqslant\mathrm{5}\:{then}\:{no}\:{general}\:{algebraic} \\ $$$${solution}\:{exists}\:{for}\:\left(\ast\right),\:{according}\:{to} \\ $$$${the}\:{Abel}−{Ruffini}\:{theorem}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com