Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 5237 by sanusihammed last updated on 02/May/16

find the domain and range of y = [_( 4x^2 +3 x <2) ^( 3x−1 x ≥ 2)

$${find}\:{the}\:{domain}\:{and}\:{range}\:{of}\: \\ $$ $${y}\:=\:\left[_{\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:<\mathrm{2}} ^{\:\mathrm{3}{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\geqslant\:\mathrm{2}} \right. \\ $$

Answered by FilupSmith last updated on 02/May/16

Domain = {x: −∞≤x≤∞} Range_1 y=3x−1 {y: [3(2)−1]≤y≤∞} {y: 5≤y≤∞} Range_2 y=4x^2 +3 {y: −∞≤y<[4(2)^2 +3]} {y: −∞≤y<19} ∴Range = {y: −∞≤y≤∞}

$${Domain}\:=\:\left\{{x}:\:−\infty\leqslant{x}\leqslant\infty\right\} \\ $$ $$ \\ $$ $${Range}_{\mathrm{1}} \:{y}=\mathrm{3}{x}−\mathrm{1} \\ $$ $$\left\{{y}:\:\left[\mathrm{3}\left(\mathrm{2}\right)−\mathrm{1}\right]\leqslant{y}\leqslant\infty\right\} \\ $$ $$\left\{{y}:\:\mathrm{5}\leqslant{y}\leqslant\infty\right\} \\ $$ $$ \\ $$ $${Range}_{\mathrm{2}} \:{y}=\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3} \\ $$ $$\left\{{y}:\:−\infty\leqslant{y}<\left[\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}\right]\right\} \\ $$ $$\left\{{y}:\:−\infty\leqslant{y}<\mathrm{19}\right\} \\ $$ $$ \\ $$ $$\therefore{Range}\:=\:\left\{{y}:\:−\infty\leqslant{y}\leqslant\infty\right\} \\ $$

Answered by Rasheed Soomro last updated on 02/May/16

y = [_( 4x^2 +3 x <2) ^( 3x−1 x ≥ 2) The function is defined for all real numbers. Hence domain of function is R. ^• For x≥2 x≥2 ⇒3x≥6 ⇒3x−1≥5 ⇒ y≥5 ^(• ) For x<2 x<2 ⇒x^2 <4 ⇒4x^2 <16 ⇒4x^2 +3<19 ⇒ y<19 So the range is {y ∣ y∈ R ∧ 5≤y<19 }

$${y}\:=\:\left[_{\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:<\mathrm{2}} ^{\:\mathrm{3}{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\geqslant\:\mathrm{2}} \right. \\ $$ $$\mathrm{The}\:\mathrm{function}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{all}\:\mathrm{real} \\ $$ $$\mathrm{numbers}.\:\mathrm{Hence}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{function}\: \\ $$ $$\mathrm{is}\:\mathbb{R}. \\ $$ $$\:^{\bullet} \mathrm{For}\:\mathrm{x}\geqslant\mathrm{2} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\mathrm{x}\geqslant\mathrm{2} \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{3x}\geqslant\mathrm{6} \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{3x}−\mathrm{1}\geqslant\mathrm{5} \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{y}\geqslant\mathrm{5} \\ $$ $$\:^{\bullet\:} \mathrm{For}\:\mathrm{x}<\mathrm{2} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\mathrm{x}<\mathrm{2} \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{2}} <\mathrm{4} \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{4x}^{\mathrm{2}} <\mathrm{16} \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{3}<\mathrm{19} \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{y}<\mathrm{19} \\ $$ $$\mathrm{So}\:\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:\left\{\mathrm{y}\:\mid\:\mathrm{y}\in\:\mathbb{R}\:\wedge\:\:\mathrm{5}\leqslant\mathrm{y}<\mathrm{19}\:\right\} \\ $$

Commented byYozzii last updated on 02/May/16

y≥3. Do a sketch graph for y to see this.

$${y}\geqslant\mathrm{3}.\:{Do}\:{a}\:{sketch}\:{graph}\:{for}\:{y}\:{to}\:{see} \\ $$ $${this}. \\ $$

Commented byFilupSmith last updated on 02/May/16

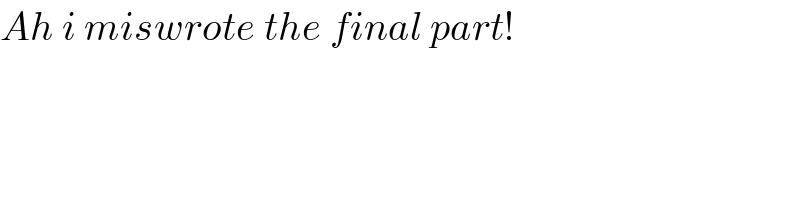
Ah i miswrote the final part!

$${Ah}\:{i}\:{miswrote}\:{the}\:{final}\:{part}! \\ $$

Commented byRasheed Soomro last updated on 06/May/16

From graph I understand now that the range is {y: y∈R,y≥3} Credit goes to Yozzi. I think that for determining range of a function its minima and maxima should be considered.

$$\mathrm{From}\:\mathrm{graph}\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{that}\:\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:\left\{{y}:\:{y}\in\mathbb{R},{y}\geqslant\mathrm{3}\right\} \\ $$ $$\mathrm{Credit}\:\mathrm{goes}\:\mathrm{to}\:\mathrm{Yozzi}. \\ $$ $$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{for}\:\mathrm{determining}\:\mathrm{range}\:\mathrm{of}\: \\ $$ $$\mathrm{a}\:\mathrm{function}\:\mathrm{its}\:\mathrm{minima}\:\mathrm{and}\:\mathrm{maxima}\:\mathrm{should} \\ $$ $$\mathrm{be}\:\mathrm{considered}. \\ $$

Commented byRasheed Soomro last updated on 05/May/16

Commented byYozzii last updated on 06/May/16

You also need to then find out whether those stationary points are global or local for all real x. If these points are global then you would have found one end of the interval for y.

$${You}\:{also}\:{need}\:{to}\:{then}\:{find}\:{out}\:{whether} \\ $$ $${those}\:{stationary}\:{points}\:{are}\:{global} \\ $$ $${or}\:{local}\:{for}\:{all}\:{real}\:{x}.\:{If}\:{these}\:{points} \\ $$ $${are}\:{global}\:{then}\:{you}\:{would}\:{have}\:{found} \\ $$ $${one}\:{end}\:{of}\:{the}\:{interval}\:{for}\:{y}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com