
Question and Answers Forum
Question Number 52459 by Abdo msup. last updated on 08/Jan/19
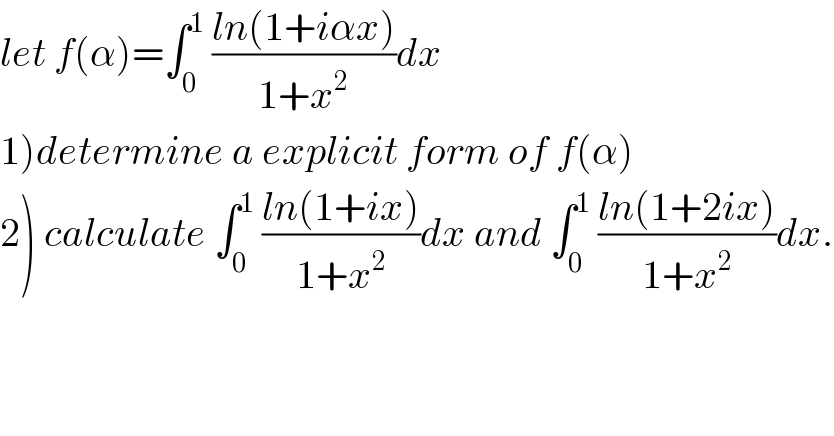
Commented by maxmathsup by imad last updated on 08/Jan/19
![1) we have f^′ (α) =∫_0 ^1 ((ix)/((1+iαx)(1+x^2 )))dx so for α≠0 f^′ (α)=(1/α) ∫_0 ^1 ((1+iαx−1)/((1+iαx)(x^2 +1)))dx =(1/α) −(1/α) ∫_0 ^1 (dx/((iαx+1)(x^2 +1)))dx let decompose F(x)=(1/((iαx+1)(x^2 +1))) ⇒ F(x)=(a/(iαx+1)) +((bx+c)/(x^2 +1)) a=lim_(x→((−1)/(iα))) (iαx+1)F(x) = (1/((((1/(iα )))^2 +1))) =(1/((1/(−α^2 ))+1)) =−(1/(1−α^2 )) α^2 =(α^2 /(α^2 −1)) lim_(x→+∞ ) xF(x)=0 =(a/(iα)) +b ⇒b=−(a/(iα)) =((ia)/α) ⇒ F(x)=(α^2 /(α^2 −1)) (1/(iαx+1)) +((((ia)/α)x+c)/(x^2 +1)) (we suppose α≠+^− 1) F(o)=1 =(α^2 /(α^2 −1)) +c ⇒c=1−(α^2 /(α^2 −1)) =((−1)/(α^2 −1)) ⇒ F(x) =(α^2 /((α^2 −1)(1+iαx))) +(((i/α)(α^2 /(α^2 −1))x−(1/(α^2 −1)))/(x^2 +1)) =(α^2 /((α^2 −1)(1+iαx))) +(1/(α^2 −1)) ((iαx−1)/(x^2 +1)) ⇒ f^′ (α)=(1/α) −(1/α) ∫_0 ^1 (α^2 /((α^2 −1)(1+iαx))) dx−(1/(α(α^2 −1))) ∫_0 ^1 ((iαx −1)/(x^2 +1))dx =(1/α) −(α/(α^2 −1))(1/(iα)) ∫_0 ^1 ((iαdx)/(1+iαx)) dx −(i/(2(α^2 −1)))[ln(x^2 +1)]_0 ^1 +(π/(4α(α^2 −1))) =(1/α) +(i/(α^2 −1))ln(1+iα) −((iln(2))/(2(α^2 −1))) +(π/(4α(α^2 −1))) ⇒ f(α) =ln∣α∣ +i ∫ ((ln(1+iα))/(α^2 −1))dα +i((ln(2))/2) ∫ (dα/(α^2 −1)) +(π/4) ∫ (dα/(α(α^2 −1))) +c but ∫ (dα/(α^2 −1)) =(1/2) ∫ ((1/(α−1)) −(1/(α+1)))dα =(1/2)ln∣((α−1)/(α+1))∣ let decompose w(α)=(1/(α(α^2 −1))) =(1/(α(α−1)(α+1))) w(α)=(a/α) +(b/(α−1)) +(c/(α+1)) ⇒a =−1 b=(1/2) and c=(1/2) ⇒w(α)=−(1/α) +(1/(2(α−1))) +(1/(2(α+1))) ⇒ ∫ (dα/(α(α^2 −1))) =−ln∣α∣ +(1/2)ln∣α^2 −1∣ ⇒ f(α)=i ∫ ((ln(1+iα))/(α^2 −1))dα +((iln(2))/4)ln∣((α−1)/(α+1))∣+ (1−(π/4))ln∣α∣+(π/8)ln∣α^2 −1∣ +c](Q52483.png)
Commented by Abdo msup. last updated on 08/Jan/19
![2) we have 1+ix=(√(1+x^2 ))((1/(√(1+x^2 ))) +i(x/(√(1+x^2 ))))=r e^(iθ) ⇒ r=(√(1+x^2 )) and θ=arctanx ⇒ ln(1+ix)=(1/2)ln(1+x^2 )+iarctanx ⇒ ∫_0 ^1 ((ln(1+ix))/(1+x^2 )) =(1/2) ∫_0 ^1 ((ln(1+x^2 ))/(1+x^2 )) dx +i∫_0 ^1 ((arctanx)/(1+x^2 ))dx by parts I=∫_0 ^1 ((arctanx)/(1+x^2 ))dx=[arctan^2 x]_0 ^1 −∫_0 ^1 ((arctanx)/(1+x^2 )) =(π^2 /(16)) −I ⇒2I=(π^2 /(16)) ⇒I=(π^2 /(32)) let find ∫_0 ^1 ((ln(1+x^2 ))/(1+x^2 )) dx let f(t)=∫_0 ^1 ((ln(1+tx^2 ))/(1+x^2 )) dx with t>0 we have f^′ (t) = ∫_0 ^1 (x^2 /((1+tx^2 )(1+x^2 )))dx =_((√t)x=u) ∫_0 ^(√t) (u^2 /(t(1+u^2 )(1+(u^2 /t)))) (du/(√t)) =(1/(√t)) ∫_0 ^(√t) (u^2 /((u^2 +1)(u^2 +t))) du let decompose F(u) =(u^2 /((u^2 +1)(u^2 +t))) ⇒ F(u)=((au +b)/(u^2 +1)) +((cu+d)/(u^2 +t)) F(−u)=F(u) ⇒((−au+b)/(u^2 +1)) +((−cu +d)/(u^2 +t)) =F(u) ⇒a=0 and c=0 ⇒ F(u)=(b/(u^2 +1)) +(d/(u^2 +t)) we see that F(u)=(1/(t−1))((1/(u^2 +1))−(1/(u^2 +t))) ⇒ ∫_0 ^(√t) F(u)du =(1/(t−1)) ∫_0 ^(√t) (du/(u^2 +1)) −(1/(t−1)) ∫_0 ^(√t) (du/(u^2 +t)) but ∫_0 ^(√t) (du/(1+u^2 )) =arctan((√t)) ∫_0 ^(√t) (du/(u^2 +t)) =_(u=(√t)α) ∫_0 ^1 (((√t)dα)/(t(1+α^2 ))) =(1/(√t))(π/4) ⇒ f^′ (t)=(1/(√t)){((arctan((√t)))/(t−1)) −(π/(4(√t)(t−1)))} ⇒ f(t) =∫ ((arctan((√t)))/((√t)(t−1)))dy −(π/4) ∫ (dt/(t(t−1))) +C ∫ (dt/(t(t−1))) =∫ ((1/(t−1)) −(1/t))dt=ln∣((t−1)/t)∣ +c_1 ∫ ((arctan((√t)))/((√t)(t−1)))dt =_((√t)=u) ∫ ((arctan(u))/(u(u^2 −1))) (2u)du =2 ∫ ((arctan(u))/(u^2 −1)) du ....be continued...](Q52497.png)
| ||
Question and Answers Forum | ||
Question Number 52459 by Abdo msup. last updated on 08/Jan/19 | ||
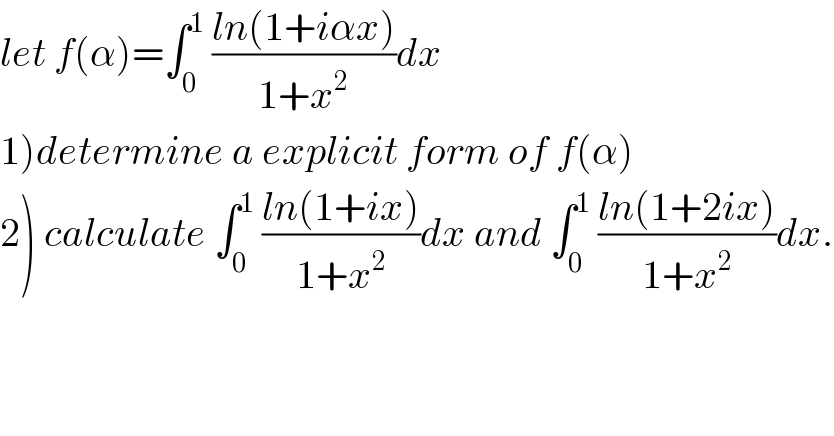 | ||
Commented by maxmathsup by imad last updated on 08/Jan/19 | ||
![1) we have f^′ (α) =∫_0 ^1 ((ix)/((1+iαx)(1+x^2 )))dx so for α≠0 f^′ (α)=(1/α) ∫_0 ^1 ((1+iαx−1)/((1+iαx)(x^2 +1)))dx =(1/α) −(1/α) ∫_0 ^1 (dx/((iαx+1)(x^2 +1)))dx let decompose F(x)=(1/((iαx+1)(x^2 +1))) ⇒ F(x)=(a/(iαx+1)) +((bx+c)/(x^2 +1)) a=lim_(x→((−1)/(iα))) (iαx+1)F(x) = (1/((((1/(iα )))^2 +1))) =(1/((1/(−α^2 ))+1)) =−(1/(1−α^2 )) α^2 =(α^2 /(α^2 −1)) lim_(x→+∞ ) xF(x)=0 =(a/(iα)) +b ⇒b=−(a/(iα)) =((ia)/α) ⇒ F(x)=(α^2 /(α^2 −1)) (1/(iαx+1)) +((((ia)/α)x+c)/(x^2 +1)) (we suppose α≠+^− 1) F(o)=1 =(α^2 /(α^2 −1)) +c ⇒c=1−(α^2 /(α^2 −1)) =((−1)/(α^2 −1)) ⇒ F(x) =(α^2 /((α^2 −1)(1+iαx))) +(((i/α)(α^2 /(α^2 −1))x−(1/(α^2 −1)))/(x^2 +1)) =(α^2 /((α^2 −1)(1+iαx))) +(1/(α^2 −1)) ((iαx−1)/(x^2 +1)) ⇒ f^′ (α)=(1/α) −(1/α) ∫_0 ^1 (α^2 /((α^2 −1)(1+iαx))) dx−(1/(α(α^2 −1))) ∫_0 ^1 ((iαx −1)/(x^2 +1))dx =(1/α) −(α/(α^2 −1))(1/(iα)) ∫_0 ^1 ((iαdx)/(1+iαx)) dx −(i/(2(α^2 −1)))[ln(x^2 +1)]_0 ^1 +(π/(4α(α^2 −1))) =(1/α) +(i/(α^2 −1))ln(1+iα) −((iln(2))/(2(α^2 −1))) +(π/(4α(α^2 −1))) ⇒ f(α) =ln∣α∣ +i ∫ ((ln(1+iα))/(α^2 −1))dα +i((ln(2))/2) ∫ (dα/(α^2 −1)) +(π/4) ∫ (dα/(α(α^2 −1))) +c but ∫ (dα/(α^2 −1)) =(1/2) ∫ ((1/(α−1)) −(1/(α+1)))dα =(1/2)ln∣((α−1)/(α+1))∣ let decompose w(α)=(1/(α(α^2 −1))) =(1/(α(α−1)(α+1))) w(α)=(a/α) +(b/(α−1)) +(c/(α+1)) ⇒a =−1 b=(1/2) and c=(1/2) ⇒w(α)=−(1/α) +(1/(2(α−1))) +(1/(2(α+1))) ⇒ ∫ (dα/(α(α^2 −1))) =−ln∣α∣ +(1/2)ln∣α^2 −1∣ ⇒ f(α)=i ∫ ((ln(1+iα))/(α^2 −1))dα +((iln(2))/4)ln∣((α−1)/(α+1))∣+ (1−(π/4))ln∣α∣+(π/8)ln∣α^2 −1∣ +c](Q52483.png) | ||
Commented by Abdo msup. last updated on 08/Jan/19 | ||
![2) we have 1+ix=(√(1+x^2 ))((1/(√(1+x^2 ))) +i(x/(√(1+x^2 ))))=r e^(iθ) ⇒ r=(√(1+x^2 )) and θ=arctanx ⇒ ln(1+ix)=(1/2)ln(1+x^2 )+iarctanx ⇒ ∫_0 ^1 ((ln(1+ix))/(1+x^2 )) =(1/2) ∫_0 ^1 ((ln(1+x^2 ))/(1+x^2 )) dx +i∫_0 ^1 ((arctanx)/(1+x^2 ))dx by parts I=∫_0 ^1 ((arctanx)/(1+x^2 ))dx=[arctan^2 x]_0 ^1 −∫_0 ^1 ((arctanx)/(1+x^2 )) =(π^2 /(16)) −I ⇒2I=(π^2 /(16)) ⇒I=(π^2 /(32)) let find ∫_0 ^1 ((ln(1+x^2 ))/(1+x^2 )) dx let f(t)=∫_0 ^1 ((ln(1+tx^2 ))/(1+x^2 )) dx with t>0 we have f^′ (t) = ∫_0 ^1 (x^2 /((1+tx^2 )(1+x^2 )))dx =_((√t)x=u) ∫_0 ^(√t) (u^2 /(t(1+u^2 )(1+(u^2 /t)))) (du/(√t)) =(1/(√t)) ∫_0 ^(√t) (u^2 /((u^2 +1)(u^2 +t))) du let decompose F(u) =(u^2 /((u^2 +1)(u^2 +t))) ⇒ F(u)=((au +b)/(u^2 +1)) +((cu+d)/(u^2 +t)) F(−u)=F(u) ⇒((−au+b)/(u^2 +1)) +((−cu +d)/(u^2 +t)) =F(u) ⇒a=0 and c=0 ⇒ F(u)=(b/(u^2 +1)) +(d/(u^2 +t)) we see that F(u)=(1/(t−1))((1/(u^2 +1))−(1/(u^2 +t))) ⇒ ∫_0 ^(√t) F(u)du =(1/(t−1)) ∫_0 ^(√t) (du/(u^2 +1)) −(1/(t−1)) ∫_0 ^(√t) (du/(u^2 +t)) but ∫_0 ^(√t) (du/(1+u^2 )) =arctan((√t)) ∫_0 ^(√t) (du/(u^2 +t)) =_(u=(√t)α) ∫_0 ^1 (((√t)dα)/(t(1+α^2 ))) =(1/(√t))(π/4) ⇒ f^′ (t)=(1/(√t)){((arctan((√t)))/(t−1)) −(π/(4(√t)(t−1)))} ⇒ f(t) =∫ ((arctan((√t)))/((√t)(t−1)))dy −(π/4) ∫ (dt/(t(t−1))) +C ∫ (dt/(t(t−1))) =∫ ((1/(t−1)) −(1/t))dt=ln∣((t−1)/t)∣ +c_1 ∫ ((arctan((√t)))/((√t)(t−1)))dt =_((√t)=u) ∫ ((arctan(u))/(u(u^2 −1))) (2u)du =2 ∫ ((arctan(u))/(u^2 −1)) du ....be continued...](Q52497.png) | ||