
Question and Answers Forum
Question Number 52487 by ajfour last updated on 08/Jan/19
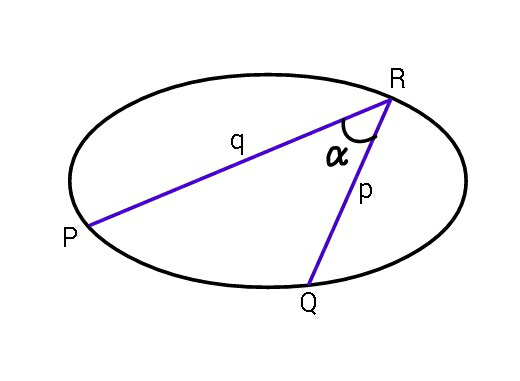
Commented by ajfour last updated on 08/Jan/19
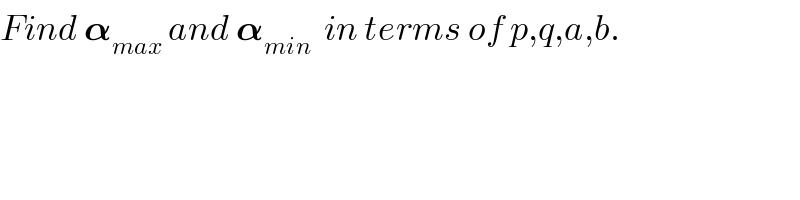
Commented by mr W last updated on 09/Jan/19
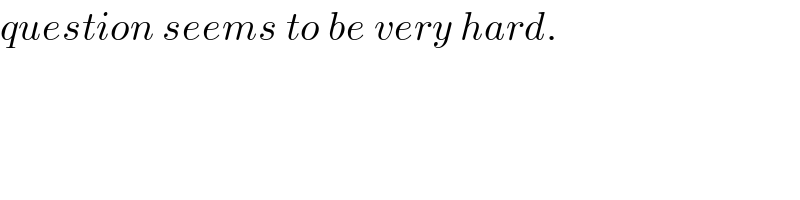
Commented by ajfour last updated on 09/Jan/19

Commented by MJS last updated on 09/Jan/19

Commented by MJS last updated on 09/Jan/19
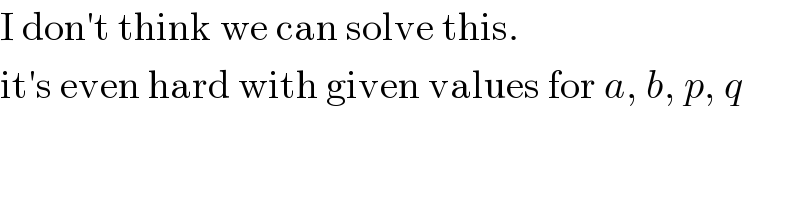
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

Commented by ajfour last updated on 09/Jan/19
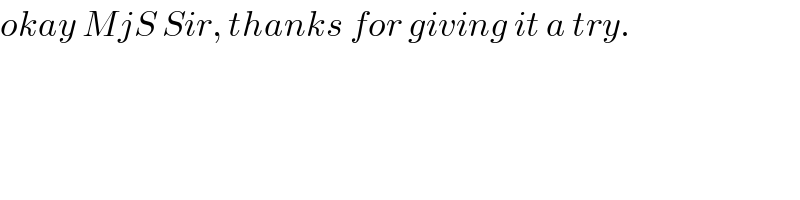
Commented by ajfour last updated on 09/Jan/19
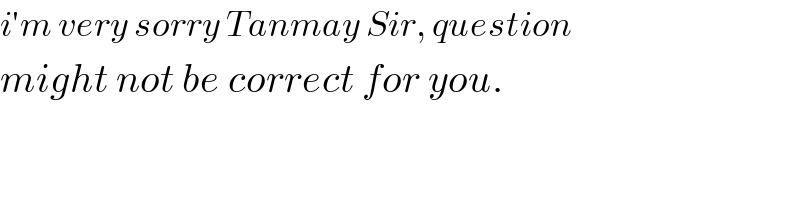
Commented by MJS last updated on 09/Jan/19
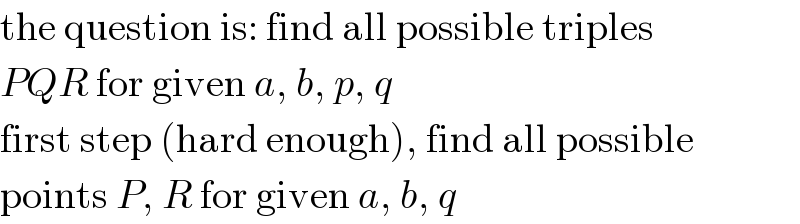
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

Commented by ajfour last updated on 09/Jan/19
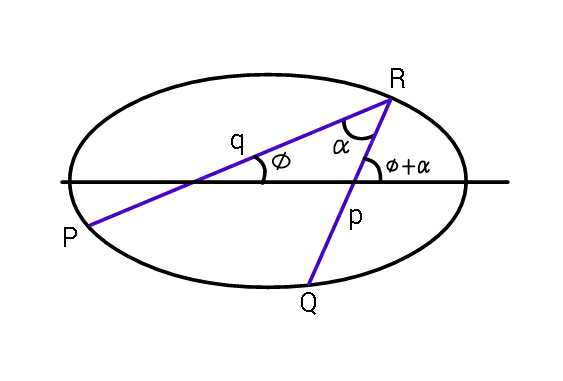
Commented by ajfour last updated on 09/Jan/19
![let R(acos θ, bsin θ) P[acos θ−pcos (θ+φ), bsin θ−psin (θ+φ)] Q(acos θ−qcos φ, bsin θ−qsin φ) let us call cos θ = c_0 , cos φ= c_1 , cos (θ+φ)=c_2 , sin θ=s_0 , sin φ= s_1 , sin (θ+φ)= s_2 . P is on ellipse, so (((ac_0 −qc_1 )^2 )/a^2 )+(((bs_0 −qs_1 )^2 )/b^2 ) = 1 ⇒ ((qc_1 ^2 )/a^2 )+((qs_1 ^2 )/b^2 ) = (2/(ab))(ac_0 c_1 +bs_0 s_1 ) similarly for Q on ellipse, ⇒ ((pc_2 ^2 )/a^2 )+((ps_2 ^2 )/b^2 ) = (2/(ab))(ac_0 c_2 +bs_0 s_2 ) _________________________ rewriting ac_0 c_1 +bs_0 s_1 = (q/(ab))(b^2 c_1 ^2 +a^2 s_1 ^2 )=(q/(ab))h_1 ac_0 c_2 +bs_0 s_2 = (p/(ab))(b^2 c_2 +a^2 s_2 ^2 )=(p/(ab))h_2 from these two eqs. c_0 = ( determinant ((((qh_1 )/(ab)),(bs_1 )),(((ph_2 )/(ab)),(bs_2 )))_ / determinant (((ac_1 ),(bs_1 )),((ac_2 ),(bs_2 )))^ ) , s_0 = ( determinant (((ac_1 ),((qh_1 )/(ab))),((ac_2 ),((ph_2 )/(ab))))_ / determinant (((ac_1 ),(bs_1 )),((ac_2 ),(bs_2 )))^ ) Now c_0 ^2 +s_0 ^2 = 1 ⇒ b^2 (((qh_1 s_2 −ph_2 s_1 )/(s_2 c_1 −c_2 s_1 )))^2 +a^2 (((ph_2 c_1 −qh_1 c_2 )/(s_2 c_1 −c_2 s_1 )))^2 = a^4 b^4 but s_2 c_1 −c_2 s_1 = sin (φ+α)cos φ−cos (φ+α)sin φ = sin α hence b^2 {qsin (φ+α)[b^2 cos^2 φ+a^2 sin^2 φ] −psin φ[b^2 cos^2 (φ+α)+a^2 sin^2 (φ+α)]}^2 +a^2 {pcos φ[b^2 cos^2 (φ+α)+a^2 sin^2 (φ+α)] −qcos (φ+α)[b^2 cos^2 φ+a^2 sin^2 φ]}^2 = a^4 b^4 sin^2 α And with (dα/dφ) = 0, φ can be obtained; hence 𝛂_(max) and 𝛂_(min) .](Q52545.png)
Commented by MJS last updated on 09/Jan/19

