Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 52627 by ajfour last updated on 10/Jan/19

Commented by ajfour last updated on 10/Jan/19

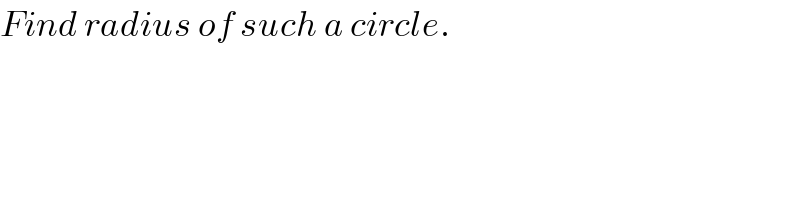
Find radius of such a circle.

$${Find}\:{radius}\:{of}\:{such}\:{a}\:{circle}. \\ $$

Answered by mr W last updated on 10/Jan/19

Q(−h,ah^2 ) y′_Q =−2ah eqn. of QP: y=ah^2 +(((x+h))/(2ah)) y=ax^2 ⇒ah^2 +((x+h)/(2ah))=ax^2 ⇒x^2 −(x/(2a^2 h))−h^2 −(1/(2a^2 ))=0 ⇒x_P =(1/2)[(1/(2a^2 h))+(√((1/(4a^4 h^2 ))+4(h^2 +(1/(2a^2 )))))] ⇒x_P =h+(1/(2a^2 h)) ⇒y_P =ah^2 +(1/(2ah))(2h+(1/(2a^2 h))) ⇒y_P =ah^2 +(1/a)+(1/(4a^3 h^2 )) PQ^2 =(h+(1/(2a^2 h))+h)^2 +(ah^2 +(1/a)+(1/(4a^3 h^2 ))−ah^2 )^2 PQ^2 =(2h+(1/(2a^2 h)))^2 +((1/a)+(1/(4a^3 h^2 )))^2 =y_P ^2 (2h+(1/(2a^2 h)))^2 +((1/a)+(1/(4a^3 h^2 )))^2 =(ah^2 +(1/a)+(1/(4a^3 h^2 )))^2 ⇒(2ah+(1/(2ah)))^2 =h^2 a^2 (2+a^2 h^2 +(1/(2a^2 h^2 ))) let λ=ah ⇒(2λ+(1/(2λ)))^2 =λ^2 (2+λ^2 +(1/(2λ^2 ))) ⇒4λ^6 −8λ^4 −6λ^2 −1=0 ⇒λ≈1.6159 ⇒R=y_P =(1/a)(1+λ^2 +(1/(4λ^2 )))≈((3.7069)/a)

$${Q}\left(−{h},{ah}^{\mathrm{2}} \right) \\ $$$${y}'_{{Q}} =−\mathrm{2}{ah} \\ $$$${eqn}.\:{of}\:{QP}: \\ $$$${y}={ah}^{\mathrm{2}} +\frac{\left({x}+{h}\right)}{\mathrm{2}{ah}} \\ $$$${y}={ax}^{\mathrm{2}} \\ $$$$\Rightarrow{ah}^{\mathrm{2}} +\frac{{x}+{h}}{\mathrm{2}{ah}}={ax}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\frac{{x}}{\mathrm{2}{a}^{\mathrm{2}} {h}}−{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{x}_{{P}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{4}} {h}^{\mathrm{2}} }+\mathrm{4}\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }\right)}\right] \\ $$$$\Rightarrow{x}_{{P}} ={h}+\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}} \\ $$$$\Rightarrow{y}_{{P}} ={ah}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{ah}}\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}}\right) \\ $$$$\Rightarrow{y}_{{P}} ={ah}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{2}} } \\ $$$${PQ}^{\mathrm{2}} =\left({h}+\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}}+{h}\right)^{\mathrm{2}} +\left({ah}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{2}} }−{ah}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${PQ}^{\mathrm{2}} =\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{2}} }\right)^{\mathrm{2}} ={y}_{{P}} ^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{2}} }\right)^{\mathrm{2}} =\left({ah}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{ah}+\frac{\mathrm{1}}{\mathrm{2}{ah}}\right)^{\mathrm{2}} ={h}^{\mathrm{2}} {a}^{\mathrm{2}} \left(\mathrm{2}+{a}^{\mathrm{2}} {h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} {h}^{\mathrm{2}} }\right) \\ $$$${let}\:\lambda={ah} \\ $$$$\Rightarrow\left(\mathrm{2}\lambda+\frac{\mathrm{1}}{\mathrm{2}\lambda}\right)^{\mathrm{2}} =\lambda^{\mathrm{2}} \left(\mathrm{2}+\lambda^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}\lambda^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\mathrm{4}\lambda^{\mathrm{6}} −\mathrm{8}\lambda^{\mathrm{4}} −\mathrm{6}\lambda^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda\approx\mathrm{1}.\mathrm{6159} \\ $$$$\Rightarrow{R}={y}_{{P}} =\frac{\mathrm{1}}{{a}}\left(\mathrm{1}+\lambda^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }\right)\approx\frac{\mathrm{3}.\mathrm{7069}}{{a}} \\ $$

Commented by mr W last updated on 11/Jan/19

Commented by ajfour last updated on 11/Jan/19

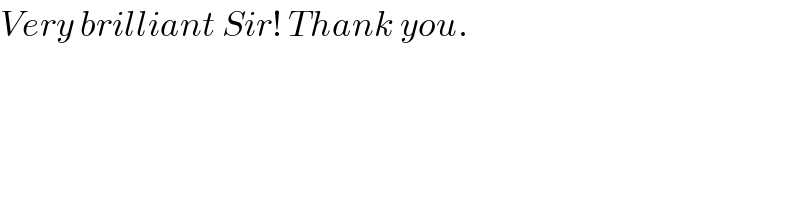
Very brilliant Sir! Thank you.

$${Very}\:{brilliant}\:{Sir}!\:{Thank}\:{you}. \\ $$

Answered by ajfour last updated on 11/Jan/19

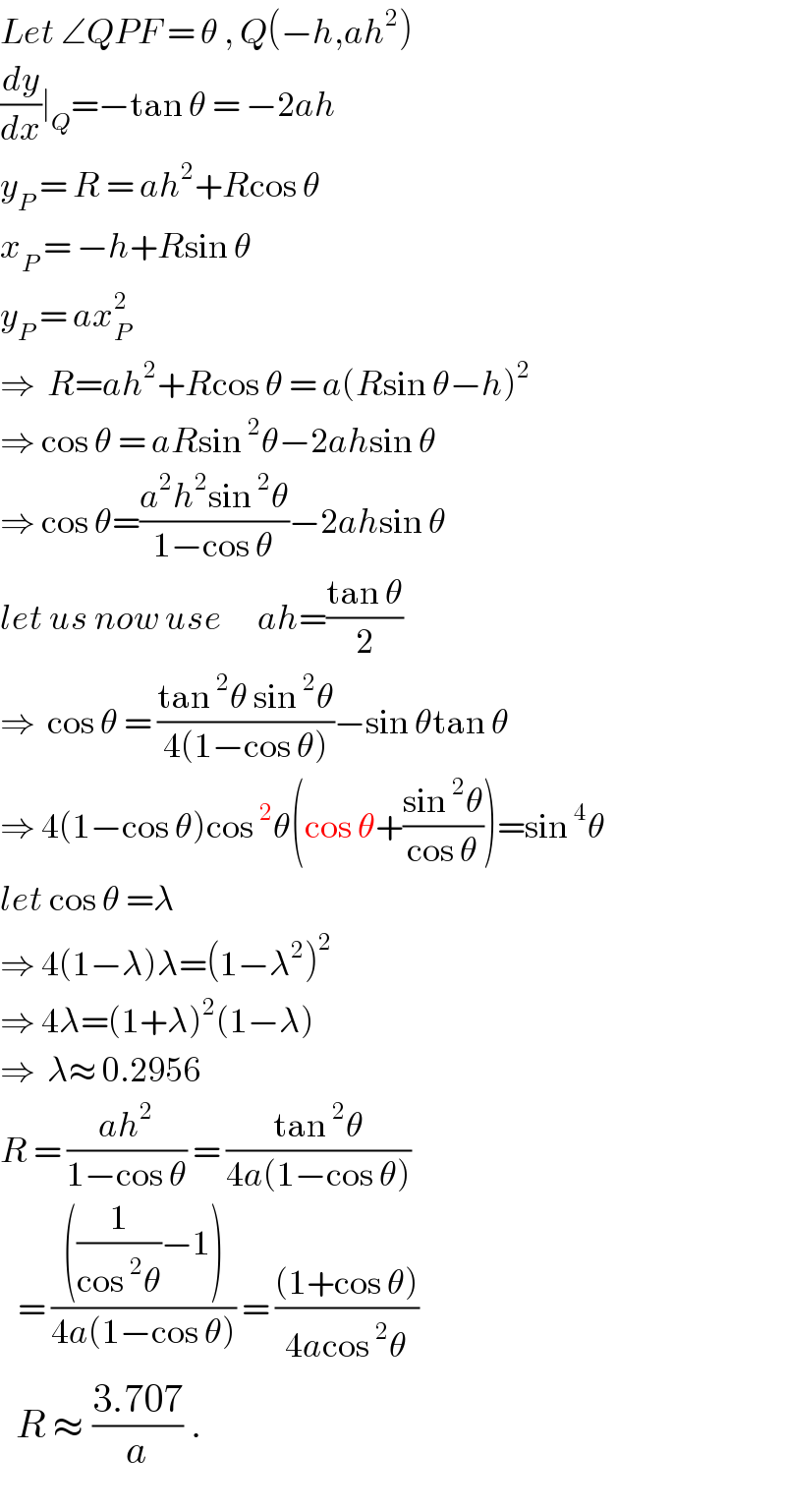
Let ∠QPF = θ , Q(−h,ah^2 ) (dy/dx)∣_Q =−tan θ = −2ah y_P = R = ah^2 +Rcos θ x_P = −h+Rsin θ y_P = ax_P ^2 ⇒ R=ah^2 +Rcos θ = a(Rsin θ−h)^2 ⇒ cos θ = aRsin^2 θ−2ahsin θ ⇒ cos θ=((a^2 h^2 sin^2 θ)/(1−cos θ))−2ahsin θ let us now use ah=((tan θ)/2) ⇒ cos θ = ((tan^2 θ sin^2 θ)/(4(1−cos θ)))−sin θtan θ ⇒ 4(1−cos θ)cos^2 θ(cos θ+((sin^2 θ)/(cos θ)))=sin^4 θ let cos θ =λ ⇒ 4(1−λ)λ=(1−λ^2 )^2 ⇒ 4λ=(1+λ)^2 (1−λ) ⇒ λ≈ 0.2956 R = ((ah^2 )/(1−cos θ)) = ((tan^2 θ)/(4a(1−cos θ))) = ((((1/(cos^2 θ))−1))/(4a(1−cos θ))) = (((1+cos θ))/(4acos^2 θ)) R ≈ ((3.707)/a) .

$${Let}\:\angle{QPF}\:=\:\theta\:,\:{Q}\left(−{h},{ah}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}\mid_{{Q}} =−\mathrm{tan}\:\theta\:=\:−\mathrm{2}{ah} \\ $$$${y}_{{P}} \:=\:{R}\:=\:{ah}^{\mathrm{2}} +{R}\mathrm{cos}\:\theta \\ $$$${x}_{{P}} \:=\:−{h}+{R}\mathrm{sin}\:\theta \\ $$$${y}_{{P}} \:=\:{ax}_{{P}} ^{\mathrm{2}} \: \\ $$$$\Rightarrow\:\:{R}={ah}^{\mathrm{2}} +{R}\mathrm{cos}\:\theta\:=\:{a}\left({R}\mathrm{sin}\:\theta−{h}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta\:=\:{aR}\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{2}{ah}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta=\frac{{a}^{\mathrm{2}} {h}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{1}−\mathrm{cos}\:\theta}−\mathrm{2}{ah}\mathrm{sin}\:\theta \\ $$$${let}\:{us}\:{now}\:{use}\:\:\:\:\:\:{ah}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{tan}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}−\mathrm{sin}\:\theta\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:\theta}\right)=\mathrm{sin}\:^{\mathrm{4}} \theta \\ $$$${let}\:\mathrm{cos}\:\theta\:=\lambda \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{1}−\lambda\right)\lambda=\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{4}\lambda=\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} \left(\mathrm{1}−\lambda\right) \\ $$$$\Rightarrow\:\:\lambda\approx\:\mathrm{0}.\mathrm{2956} \\ $$$${R}\:=\:\frac{{ah}^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}\:\theta}\:=\:\frac{\mathrm{tan}\:^{\mathrm{2}} \theta}{\mathrm{4}{a}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)} \\ $$$$\:\:\:=\:\frac{\left(\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \theta}−\mathrm{1}\right)}{\mathrm{4}{a}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}\:=\:\frac{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{\mathrm{4}{a}\mathrm{cos}\:^{\mathrm{2}} \theta}\: \\ $$$$\:\:{R}\:\approx\:\frac{\mathrm{3}.\mathrm{707}}{{a}}\:. \\ $$

Commented by mr W last updated on 11/Jan/19

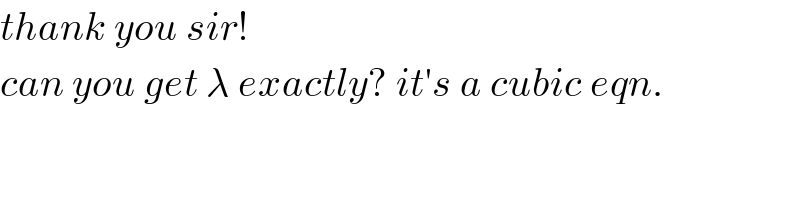
thank you sir! can you get λ exactly? it′s a cubic eqn.

$${thank}\:{you}\:{sir}! \\ $$$${can}\:{you}\:{get}\:\lambda\:{exactly}?\:{it}'{s}\:{a}\:{cubic}\:{eqn}. \\ $$

Commented by ajfour last updated on 12/Jan/19

Thanks sir, i meant i tried but couldn′t match with the calculated answer in one attempt.

$${Thanks}\:{sir},\:{i}\:{meant}\:{i}\:{tried}\:{but} \\ $$$${couldn}'{t}\:{match}\:{with}\:{the}\:{calculated} \\ $$$${answer}\:{in}\:{one}\:{attempt}. \\ $$

Commented by ajfour last updated on 11/Jan/19

no sir, how come ?

$${no}\:{sir},\:{how}\:{come}\:? \\ $$

Commented by mr W last updated on 11/Jan/19

4λ=(1+λ)^2 (1−λ) ⇒λ^3 +λ^2 +3λ−1=0 (cubic eqn.) let λ=t+δ t^3 +(3δ+1)t^2 +(3δ^2 +2δ+3)t+δ^3 +δ^2 +3δ−1=0 let 3δ+1=0⇒δ=−(1/3) ⇒t^3 +(8/3)t−((52)/(27))=0 (u+v)^3 −3uv(u+v)−(u^3 +v^3 )=0 let t=u+v −3uv=(8/3) ⇒u^3 v^3 =−((512)/(729)) ⇒u^3 +v^3 =((52)/(27)) u^3 and v^3 are roots of x^2 −((52)/(27))x−((512)/(729))=0 x=((2(13±3(√(33))))/(27))=u^3 and v^3 ⇒u=(((2(13+3(√(33)))))^(1/3) /3) ⇒v=(((2(13−3(√(33)))))^(1/3) /3) ⇒λ=t+δ=u+v+δ ⇒λ=((((2(13+3(√(33)))))^(1/3) +((2(13−3(√(33)))))^(1/3) −1)/3)≈0.295598

$$\mathrm{4}\lambda=\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} \left(\mathrm{1}−\lambda\right) \\ $$$$\Rightarrow\lambda^{\mathrm{3}} +\lambda^{\mathrm{2}} +\mathrm{3}\lambda−\mathrm{1}=\mathrm{0}\:\:\:\left({cubic}\:{eqn}.\right) \\ $$$${let}\:\lambda={t}+\delta \\ $$$${t}^{\mathrm{3}} +\left(\mathrm{3}\delta+\mathrm{1}\right){t}^{\mathrm{2}} +\left(\mathrm{3}\delta^{\mathrm{2}} +\mathrm{2}\delta+\mathrm{3}\right){t}+\delta^{\mathrm{3}} +\delta^{\mathrm{2}} +\mathrm{3}\delta−\mathrm{1}=\mathrm{0} \\ $$$${let}\:\mathrm{3}\delta+\mathrm{1}=\mathrm{0}\Rightarrow\delta=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +\frac{\mathrm{8}}{\mathrm{3}}{t}−\frac{\mathrm{52}}{\mathrm{27}}=\mathrm{0} \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} −\mathrm{3}{uv}\left({u}+{v}\right)−\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$${let}\:{t}={u}+{v} \\ $$$$−\mathrm{3}{uv}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\Rightarrow{u}^{\mathrm{3}} {v}^{\mathrm{3}} =−\frac{\mathrm{512}}{\mathrm{729}} \\ $$$$\Rightarrow{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\frac{\mathrm{52}}{\mathrm{27}} \\ $$$${u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \:{are}\:{roots}\:{of} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{52}}{\mathrm{27}}{x}−\frac{\mathrm{512}}{\mathrm{729}}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{13}\pm\mathrm{3}\sqrt{\mathrm{33}}\right)}{\mathrm{27}}={u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \\ $$$$\Rightarrow{u}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}\left(\mathrm{13}+\mathrm{3}\sqrt{\mathrm{33}}\right)}}{\mathrm{3}} \\ $$$$\Rightarrow{v}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}\left(\mathrm{13}−\mathrm{3}\sqrt{\mathrm{33}}\right)}}{\mathrm{3}} \\ $$$$\Rightarrow\lambda={t}+\delta={u}+{v}+\delta \\ $$$$\Rightarrow\lambda=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}\left(\mathrm{13}+\mathrm{3}\sqrt{\mathrm{33}}\right)}+\sqrt[{\mathrm{3}}]{\mathrm{2}\left(\mathrm{13}−\mathrm{3}\sqrt{\mathrm{33}}\right)}−\mathrm{1}}{\mathrm{3}}\approx\mathrm{0}.\mathrm{295598} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com