Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 52663 by ajfour last updated on 11/Jan/19

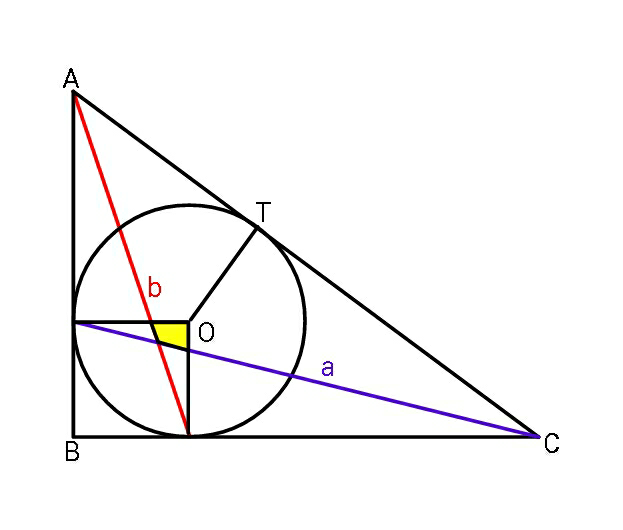
Commented by ajfour last updated on 11/Jan/19

$F i n d r a d i u s R i n t e r m s o f a a n d b .$ $A l s o f i n d t h e c e n t r a l a r e a i n y e l l o w$ $i n t e r m s o f a a n d b . (s o u r c e : a j f o u r)$
	Answered by mr W last updated on 11/Jan/19

	$(a^{2} - r^{2}) + (b^{2} - r^{2}) = {(\sqrt{a^{2} - r^{2}} - r + \sqrt{b^{2} - r^{2}} - r)}^{2}$ $a^{2} + b^{2} - 2 r^{2} = {(\sqrt{a^{2} - r^{2}} + \sqrt{b^{2} - r^{2}} - 2 r)}^{2}$ $a^{2} + b^{2} - 2 r^{2} = a^{2} - r^{2} + b^{2} - r^{2} + 4 r^{2} + 2 [\sqrt{(a^{2} - r^{2}) (b^{2} - r^{2})} - 2 r (\sqrt{a^{2} - r^{2}} + \sqrt{b^{2} - r^{2}})]$ $\Rightarrow \sqrt{(a^{2} - r^{2}) (b^{2} - r^{2})} = 2 r (\sqrt{a^{2} - r^{2}} + \sqrt{b^{2} - r^{2}} - r)$ $e x a m p l e :$ $a = 3, b = 4 \Rightarrow r = 0.9569$
	Commented by ajfour last updated on 11/Jan/19

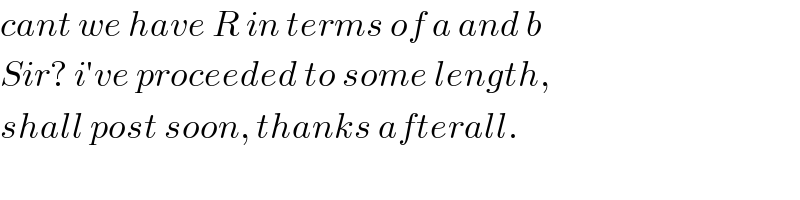
	$c a n t w e h a v e R i n t e r m s o f a a n d b$ $S i r ? i^{'} v e p r o c e e d e d t o s o m e l e n g t h,$ $s h a l l p o s t s o o n, t h a n k s a f t e r a l l .$
	Answered by ajfour last updated on 18/Jan/19
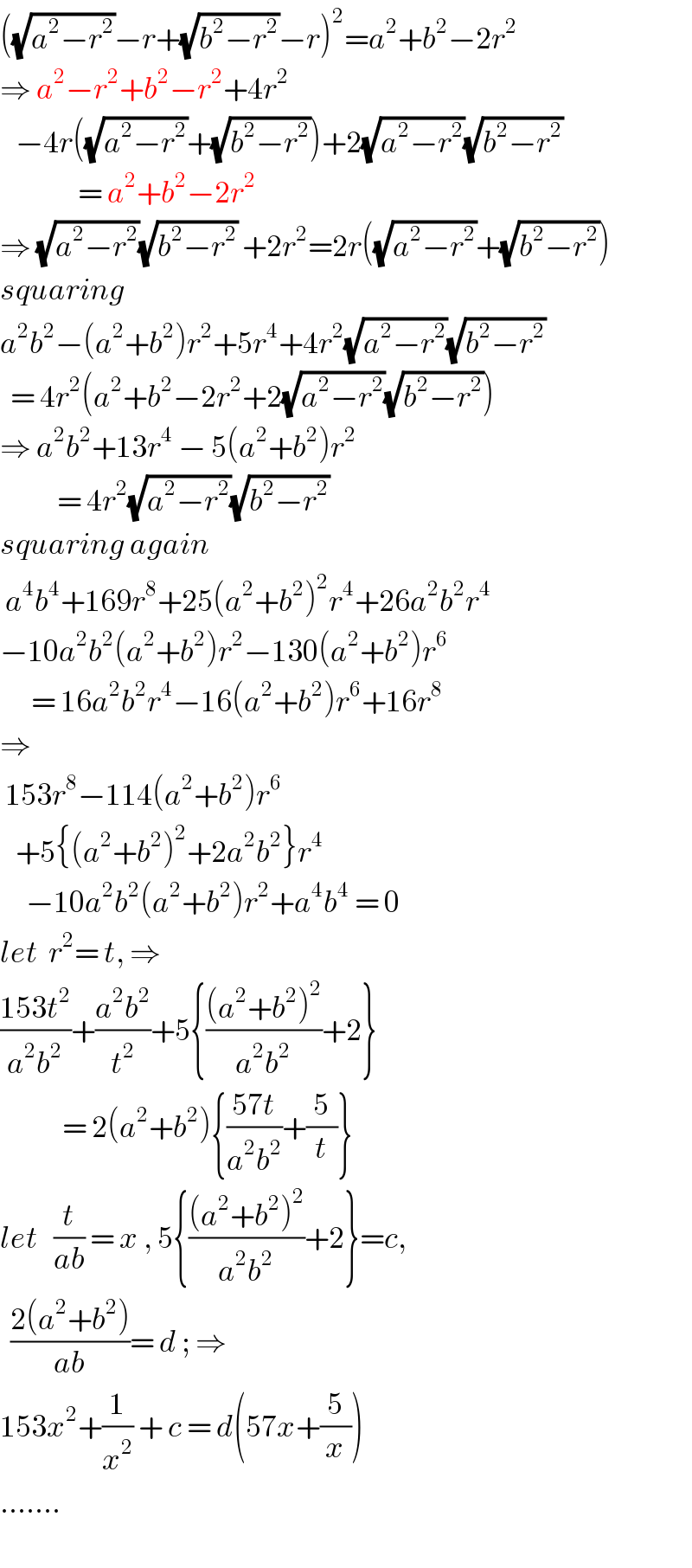
	$((√(a^2 −r^2 ))−r+(√(b^2 −r^2 ))−r)^2 =a^2 +b^2 −2r^2 ⇒ a^2 −r^2 +b^2 −r^2 +4r^2 −4r((√(a^2 −r^2 ))+(√(b^2 −r^2 )))+2(√(a^2 −r^2 ))(√(b^2 −r^2 )) = a^2 +b^2 −2r^2 ⇒ (√(a^2 −r^2 ))(√(b^2 −r^2 )) +2r^2 =2r((√(a^2 −r^2 ))+(√(b^2 −r^2 ))) squaring a^2 b^2 −(a^2 +b^2 )r^2 +5r^4 +4r^2 (√(a^2 −r^2 ))(√(b^2 −r^2 )) = 4r^2 (a^2 +b^2 −2r^2 +2(√(a^2 −r^2 ))(√(b^2 −r^2 ))) ⇒ a^2 b^2 +13r^4 − 5(a^2 +b^2 )r^2 = 4r^2 (√(a^2 −r^2 ))(√(b^2 −r^2 )) squaring again a^4 b^4 +169r^8 +25(a^2 +b^2 )^2 r^4 +26a^2 b^2 r^4 −10a^2 b^2 (a^2 +b^2 )r^2 −130(a^2 +b^2 )r^6 = 16a^2 b^2 r^4 −16(a^2 +b^2 )r^6 +16r^8 ⇒ 153r^8 −114(a^2 +b^2 )r^6 +5{(a^2 +b^2 )^2 +2a^2 b^2 }r^4 −10a^2 b^2 (a^2 +b^2 )r^2 +a^4 b^4 = 0 let r^2 = t, ⇒ ((153t^2 )/(a^2 b^2 ))+((a^2 b^2 )/t^2 )+5{(((a^2 +b^2 )^2 )/(a^2 b^2 ))+2} = 2(a^2 +b^2 ){((57t)/(a^2 b^2 ))+(5/t)} let (t/(ab)) = x , 5{(((a^2 +b^2 )^2 )/(a^2 b^2 ))+2}=c, ((2(a^2 +b^2 ))/(ab))= d ; ⇒ 153x^2 +(1/x^2 ) + c = d(57x+(5/x)) .......$
	${(\sqrt{a^{2} - r^{2}} - r + \sqrt{b^{2} - r^{2}} - r)}^{2} = a^{2} + b^{2} - 2 r^{2}$ $\Rightarrow a^{2} - r^{2} + b^{2} - r^{2} + 4 r^{2}$ $- 4 r (\sqrt{a^{2} - r^{2}} + \sqrt{b^{2} - r^{2}}) + 2 \sqrt{a^{2} - r^{2}} \sqrt{b^{2} - r^{2}}$ $= a^{2} + b^{2} - 2 r^{2}$ $\Rightarrow \sqrt{a^{2} - r^{2}} \sqrt{b^{2} - r^{2}} + 2 r^{2} = 2 r (\sqrt{a^{2} - r^{2}} + \sqrt{b^{2} - r^{2}})$ $s q u a r i n g$ $a^{2} b^{2} - (a^{2} + b^{2}) r^{2} + 5 r^{4} + 4 r^{2} \sqrt{a^{2} - r^{2}} \sqrt{b^{2} - r^{2}}$ $= 4 r^{2} (a^{2} + b^{2} - 2 r^{2} + 2 \sqrt{a^{2} - r^{2}} \sqrt{b^{2} - r^{2}})$ $\Rightarrow a^{2} b^{2} + 13 r^{4} - 5 (a^{2} + b^{2}) r^{2}$ $= 4 r^{2} \sqrt{a^{2} - r^{2}} \sqrt{b^{2} - r^{2}}$ $s q u a r i n g a g a i n$ $a^{4} b^{4} + 169 r^{8} + 25 {(a^{2} + b^{2})}^{2} r^{4} + 26 a^{2} b^{2} r^{4}$ $- 10 a^{2} b^{2} (a^{2} + b^{2}) r^{2} - 130 (a^{2} + b^{2}) r^{6}$ $= 16 a^{2} b^{2} r^{4} - 16 (a^{2} + b^{2}) r^{6} + 16 r^{8}$ $\Rightarrow$ $153 r^{8} - 114 (a^{2} + b^{2}) r^{6}$ $+ 5 {{(a^{2} + b^{2})}^{2} + 2 a^{2} b^{2}} r^{4}$ $- 10 a^{2} b^{2} (a^{2} + b^{2}) r^{2} + a^{4} b^{4} = 0$ $l e t r^{2} = t, \Rightarrow$ $\frac{153 t^{2}}{a^{2} b^{2}} + \frac{a^{2} b^{2}}{t^{2}} + 5 {\frac{{(a^{2} + b^{2})}^{2}}{a^{2} b^{2}} + 2}$ $= 2 (a^{2} + b^{2}) {\frac{57 t}{a^{2} b^{2}} + \frac{5}{t}}$ $l e t \frac{t}{a b} = x, 5 {\frac{{(a^{2} + b^{2})}^{2}}{a^{2} b^{2}} + 2} = c,$ $\frac{2 (a^{2} + b^{2})}{a b} = d; \Rightarrow$ $153 x^{2} + \frac{1}{x^{2}} + c = d (57 x + \frac{5}{x})$ $. . . . . . .$
	Commented by ajfour last updated on 11/Jan/19

	$y e s s i r, n o t u s e f u l e t a l . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum