
Previous in Relation and Functions Next in Relation and Functions
Question Number 52671 by maxmathsup by imad last updated on 11/Jan/19
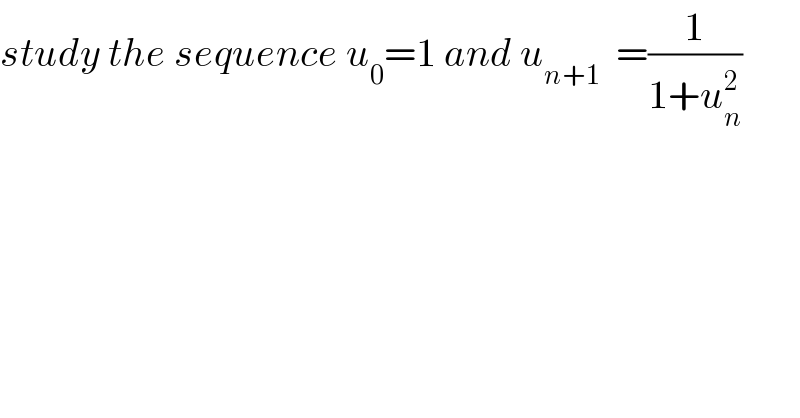
$${study}\:{the}\:{sequence}\:{u}_{\mathrm{0}} =\mathrm{1}\:{and}\:{u}_{{n}+\mathrm{1}} \:\:=\frac{\mathrm{1}}{\mathrm{1}+{u}_{{n}} ^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 11/Mar/19
![its clear that u_n >0 ∀n let prove that 0<u_n ≤1 n=0 ⇒ 0<u_o ≤1 (true) let suppose 0<u_n ≤1 ⇒ u_(n+1) −1=(1/(1+u_n ^2 )) −1 =−(u_n ^2 /(1+u_n ^2 )) ≤0 ⇒ 0<u_(n+1) ≤1 we have u_(n+1) =f(u_n ) with f(x)=(1/(1+x^2 )) (we can take x>0) ⇒f^′ (x)=−((2x)/(1+x^2 ))<0 ⇒ f is decresing x 0 +∞ f^′ (x) − f(x)1 decre 0 is f have a fixed point f(x)=x ⇒(1/(1+x^2 )) =x ⇒1 =x +x^3 ⇒x^3 +x−1 =0 let p(x) =x^3 +x−1 we have p^′ (x)=3x^2 +1>0 ⇒p is incressing p(0)=−1 <0 and p(1) =1 >0 ⇒∃! α_0 ∈]0,1[ /p(α_0 )=0 and α is the fixed point ⇒ α_0 =lim_(n→+∞) u_n](Q56197.png)
$${its}\:{clear}\:{that}\:{u}_{{n}} >\mathrm{0}\:\forall{n}\:\:\:\:{let}\:{prove}\:{that}\:\mathrm{0}<{u}_{{n}} \leqslant\mathrm{1}\: \\ $$$${n}=\mathrm{0}\:\Rightarrow\:\mathrm{0}<{u}_{{o}} \leqslant\mathrm{1}\:\left({true}\right)\:{let}\:{suppose}\:\mathrm{0}<{u}_{{n}} \leqslant\mathrm{1}\:\Rightarrow\:{u}_{{n}+\mathrm{1}} −\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}+{u}_{{n}} ^{\mathrm{2}} }\:−\mathrm{1} \\ $$$$=−\frac{{u}_{{n}} ^{\mathrm{2}} }{\mathrm{1}+{u}_{{n}} ^{\mathrm{2}} }\:\leqslant\mathrm{0}\:\Rightarrow\:\mathrm{0}<{u}_{{n}+\mathrm{1}} \leqslant\mathrm{1}\:\:{we}\:{have} \\ $$$${u}_{{n}+\mathrm{1}} ={f}\left({u}_{{n}} \right)\:\:{with}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\left({we}\:{can}\:{take}\:{x}>\mathrm{0}\right)\:\Rightarrow{f}^{'} \left({x}\right)=−\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }<\mathrm{0}\:\Rightarrow \\ $$$${f}\:{is}\:{decresing}\: \\ $$$${x}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:− \\ $$$${f}\left({x}\right)\mathrm{1}\:\:\:\:\:\:\:{decre}\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:{is}\:{f}\:{have}\:{a}\:{fixed}\:{point} \\ $$$${f}\left({x}\right)={x}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={x}\:\Rightarrow\mathrm{1}\:={x}\:+{x}^{\mathrm{3}} \:\Rightarrow{x}^{\mathrm{3}} \:+{x}−\mathrm{1}\:=\mathrm{0} \\ $$$${let}\:{p}\left({x}\right)\:={x}^{\mathrm{3}} \:+{x}−\mathrm{1}\:\:\:{we}\:{have}\:{p}^{'} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{1}>\mathrm{0}\:\Rightarrow{p}\:{is}\:{incressing} \\ $$$$\left.{p}\left(\mathrm{0}\right)=−\mathrm{1}\:<\mathrm{0}\:\:{and}\:{p}\left(\mathrm{1}\right)\:=\mathrm{1}\:>\mathrm{0}\:\Rightarrow\exists!\:\alpha_{\mathrm{0}} \:\:\in\right]\mathrm{0},\mathrm{1}\left[\:/{p}\left(\alpha_{\mathrm{0}} \right)=\mathrm{0}\:\:{and}\:\alpha\:{is}\:{the}\:{fixed}\right. \\ $$$${point}\:\:\Rightarrow\:\alpha_{\mathrm{0}} ={lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \\ $$
