
Previous in Relation and Functions Next in Relation and Functions
Question Number 52673 by maxmathsup by imad last updated on 11/Jan/19
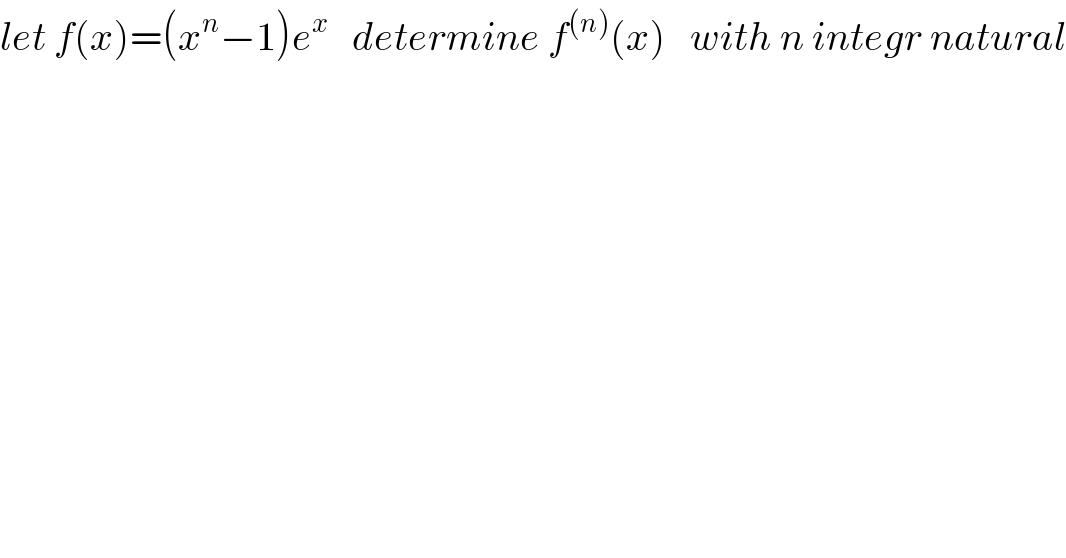
$${let}\:{f}\left({x}\right)=\left({x}^{{n}} −\mathrm{1}\right){e}^{{x}} \:\:\:{determine}\:{f}^{\left({n}\right)} \left({x}\right)\:\:\:{with}\:{n}\:{integr}\:{natural} \\ $$
Commented by maxmathsup by imad last updated on 13/Jan/19
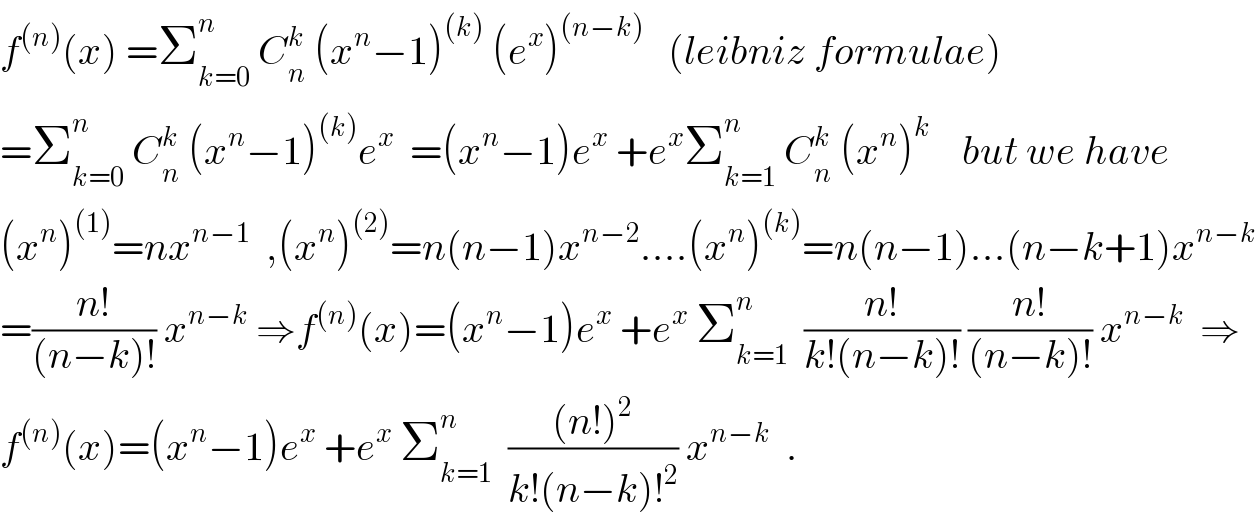
$${f}^{\left({n}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({x}^{{n}} −\mathrm{1}\right)^{\left({k}\right)} \:\left({e}^{{x}} \right)^{\left({n}−{k}\right)} \:\:\:\left({leibniz}\:{formulae}\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({x}^{{n}} −\mathrm{1}\right)^{\left({k}\right)} {e}^{{x}} \:\:=\left({x}^{{n}} −\mathrm{1}\right){e}^{{x}} \:+{e}^{{x}} \sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({x}^{{n}} \right)^{{k}} \:\:\:\:{but}\:{we}\:{have} \\ $$$$\left({x}^{{n}} \right)^{\left(\mathrm{1}\right)} ={nx}^{{n}−\mathrm{1}} \:\:,\left({x}^{{n}} \right)^{\left(\mathrm{2}\right)} ={n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} ....\left({x}^{{n}} \right)^{\left({k}\right)} ={n}\left({n}−\mathrm{1}\right)...\left({n}−{k}+\mathrm{1}\right){x}^{{n}−{k}} \\ $$$$=\frac{{n}!}{\left({n}−{k}\right)!}\:{x}^{{n}−{k}} \:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\left({x}^{{n}} −\mathrm{1}\right){e}^{{x}} \:+{e}^{{x}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{n}!}{{k}!\left({n}−{k}\right)!}\:\frac{{n}!}{\left({n}−{k}\right)!}\:{x}^{{n}−{k}} \:\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left({x}^{{n}} −\mathrm{1}\right){e}^{{x}} \:+{e}^{{x}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\left({n}!\right)^{\mathrm{2}} }{{k}!\left({n}−{k}\right)!^{\mathrm{2}} }\:{x}^{{n}−{k}} \:\:. \\ $$
Answered by Smail last updated on 11/Jan/19
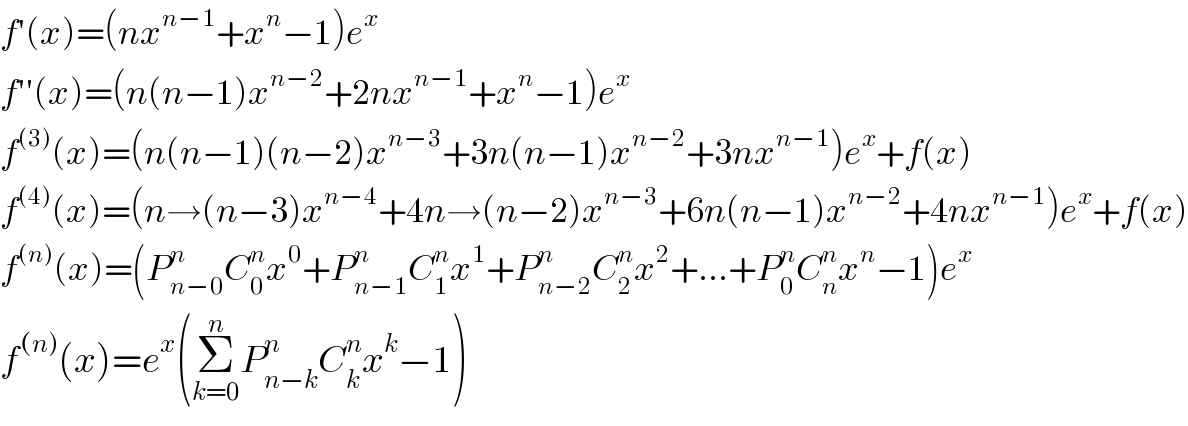
$${f}'\left({x}\right)=\left({nx}^{{n}−\mathrm{1}} +{x}^{{n}} −\mathrm{1}\right){e}^{{x}} \\ $$$${f}''\left({x}\right)=\left({n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} +\mathrm{2}{nx}^{{n}−\mathrm{1}} +{x}^{{n}} −\mathrm{1}\right){e}^{{x}} \\ $$$${f}^{\left(\mathrm{3}\right)} \left({x}\right)=\left({n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right){x}^{{n}−\mathrm{3}} +\mathrm{3}{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} +\mathrm{3}{nx}^{{n}−\mathrm{1}} \right){e}^{{x}} +{f}\left({x}\right) \\ $$$${f}^{\left(\mathrm{4}\right)} \left({x}\right)=\left({n}\rightarrow\left({n}−\mathrm{3}\right){x}^{{n}−\mathrm{4}} +\mathrm{4}{n}\rightarrow\left({n}−\mathrm{2}\right){x}^{{n}−\mathrm{3}} +\mathrm{6}{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} +\mathrm{4}{nx}^{{n}−\mathrm{1}} \right){e}^{{x}} +{f}\left({x}\right) \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left({P}_{{n}−\mathrm{0}} ^{{n}} {C}_{\mathrm{0}} ^{{n}} {x}^{\mathrm{0}} +{P}_{{n}−\mathrm{1}} ^{{n}} {C}_{\mathrm{1}} ^{{n}} {x}^{\mathrm{1}} +{P}_{{n}−\mathrm{2}} ^{{n}} {C}_{\mathrm{2}} ^{{n}} {x}^{\mathrm{2}} +...+{P}_{\mathrm{0}} ^{{n}} {C}_{{n}} ^{{n}} {x}^{{n}} −\mathrm{1}\right){e}^{{x}} \\ $$$${f}^{\left({n}\right)} \left({x}\right)={e}^{{x}} \left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{P}_{{n}−{k}} ^{{n}} {C}_{{k}} ^{{n}} {x}^{{k}} −\mathrm{1}\right) \\ $$
