
Question Number 52680 by maxmathsup by imad last updated on 11/Jan/19
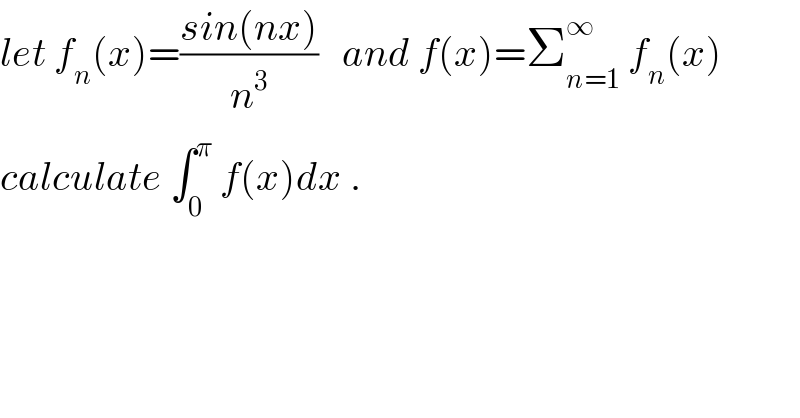
$${let}\:{f}_{{n}} \left({x}\right)=\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }\:\:\:{and}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{f}_{{n}} \left({x}\right) \\ $$$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:{f}\left({x}\right){dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 11/Jan/19
![its clear that the serie Σ f_n (x) converge simpl.and unif. because ∣f_n (x)∣≤(1/n^3 ) and Σ (1/n^3 ) converges we have ∫_0 ^π f(x)dx =∫_0 ^π Σ_(n=1) ^∞ ((sin(nx))/n^3 ) =Σ_(n=1) ^∞ (1/n^3 ) ∫_0 ^π sin(nx)dx =Σ_(n=1) ^∞ (1/n^3 )[−(1/n)cos(nx)]_0 ^π =Σ_(n=1) ^∞ (1/n^4 )(1−(−1)^n ) =2 Σ_(n=0) ^∞ (1/((2n+1)^4 )) but we have proved that Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^4 )) + (1/(16))Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒Σ_(n=0) ^∞ (1/((2n+1)^4 )) =(π^4 /(90)) −(1/(16)) (π^4 /(90)) =(1−(1/(16)))(π^4 /(90)) =((15)/(16)) (π^4 /(90)) =((3.5)/(3.30 16)) π^4 =(π^4 /(6.16)) =(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =2 .(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =(π^4 /(48)) .](Q52704.png)
$${its}\:{clear}\:{that}\:{the}\:{serie}\:\Sigma\:{f}_{{n}} \left({x}\right)\:{converge}\:{simpl}.{and}\:{unif}.\:{because} \\ $$$$\mid{f}_{{n}} \left({x}\right)\mid\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\:{and}\:\Sigma\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:{converges}\:\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\pi} \sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{\pi} \:{sin}\left({nx}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\left[−\frac{\mathrm{1}}{{n}}{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right) \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} }\:\:{but}\:{we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\:=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{\mathrm{16}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\:=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} }\:=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:−\frac{\mathrm{1}}{\mathrm{16}}\:\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}\right)\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:=\frac{\mathrm{15}}{\mathrm{16}}\:\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:=\frac{\mathrm{3}.\mathrm{5}}{\mathrm{3}.\mathrm{30}\:\mathrm{16}}\:\pi^{\mathrm{4}} \:=\frac{\pi^{\mathrm{4}} }{\mathrm{6}.\mathrm{16}}\:=\frac{\pi^{\mathrm{4}} }{\mathrm{96}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){dx}\:=\mathrm{2}\:.\frac{\pi^{\mathrm{4}} }{\mathrm{96}}\:\Rightarrow\:\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){dx}\:=\frac{\pi^{\mathrm{4}} }{\mathrm{48}}\:. \\ $$
