Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 52731 by ajfour last updated on 12/Jan/19

Commented by MJS last updated on 12/Jan/19

for b=a (circle) the equilateral triangle is the one with minimum perimeter. we can draw an equilateral triangle for a circle with r=a and then compress with the factor (a/b) [P= ((x),(y) ) → P′= ((x),(((b/a)y)) )] A′= (((acos α)),((bsin α)) ) B′= (((acos (α+120°))),((bsin (α+120°))) ) C′= (((acos (α−120°))),((bsin (α−120°))) ) now calculate the perimeter p(α) and find its min/max p′(α)=0 sorry I have no time at the moment

$$\mathrm{for}\:{b}={a}\:\left(\mathrm{circle}\right)\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{one}\:\mathrm{with}\:\mathrm{minimum}\:\mathrm{perimeter}. \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{draw}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{for}\:\mathrm{a} \\ $$$$\mathrm{circle}\:\mathrm{with}\:{r}={a}\:\mathrm{and}\:\mathrm{then}\:\mathrm{compress}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{factor}\:\frac{{a}}{{b}}\:\left[{P}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:\rightarrow\:{P}'=\begin{pmatrix}{{x}}\\{\frac{{b}}{{a}}{y}}\end{pmatrix}\right] \\ $$$$ \\ $$$${A}'=\begin{pmatrix}{{a}\mathrm{cos}\:\alpha}\\{{b}\mathrm{sin}\:\alpha}\end{pmatrix}\:\:{B}'=\begin{pmatrix}{{a}\mathrm{cos}\:\left(\alpha+\mathrm{120}°\right)}\\{{b}\mathrm{sin}\:\left(\alpha+\mathrm{120}°\right)}\end{pmatrix}\:\:{C}'=\begin{pmatrix}{{a}\mathrm{cos}\:\left(\alpha−\mathrm{120}°\right)}\\{{b}\mathrm{sin}\:\left(\alpha−\mathrm{120}°\right)}\end{pmatrix} \\ $$$$\mathrm{now}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{perimeter}\:{p}\left(\alpha\right)\:\mathrm{and}\:\mathrm{find} \\ $$$$\mathrm{its}\:\mathrm{min}/\mathrm{max}\:{p}'\left(\alpha\right)=\mathrm{0} \\ $$$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}\:\mathrm{at}\:\mathrm{the}\:\mathrm{moment} \\ $$

Commented by ajfour last updated on 12/Jan/19

The △ circumscribing the ellipse shall be of minimum perimeter in which of the two shown orientations?(if a>b) or can it be so in some other orientation(may be equilateral)? Find its sides in terms of a and b.

$${The}\:\bigtriangleup\:{circumscribing}\:{the}\:{ellipse} \\ $$$${shall}\:{be}\:{of}\:{minimum}\:{perimeter} \\ $$$${in}\:{which}\:{of}\:{the}\:{two}\:{shown} \\ $$$${orientations}?\left({if}\:{a}>{b}\right) \\ $$$${or}\:{can}\:{it}\:{be}\:{so}\:{in}\:{some}\:{other} \\ $$$${orientation}\left({may}\:{be}\:{equilateral}\right)? \\ $$$${Find}\:{its}\:{sides}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$

Commented by mr W last updated on 12/Jan/19

i think there is no other orientation than the two shown.

$${i}\:{think}\:{there}\:{is}\:{no}\:{other}\:{orientation} \\ $$$${than}\:{the}\:{two}\:{shown}. \\ $$

Commented by ajfour last updated on 12/Jan/19

please go ahead; sides of the △ Sir?

$${please}\:{go}\:{ahead};\:{sides}\:{of}\:{the}\:\bigtriangleup\:{Sir}? \\ $$

Commented by ajfour last updated on 12/Jan/19

wont the triangle sides become curvilinear by such compression, Sir ?

$${wont}\:{the}\:{triangle}\:{sides}\:{become} \\ $$$${curvilinear}\:{by}\:{such}\:{compression}, \\ $$$${Sir}\:? \\ $$

Commented by MJS last updated on 12/Jan/19

no. it′s linear y=kx+d ⇔ P= ((x),((kx+d)) ) → P′= ((x),(((b/a)(kx+d))) ) ⇔ y=((bk)/a)x+((bd)/a) straight lines stay straight lines

$$\mathrm{no}.\:\mathrm{it}'\mathrm{s}\:\mathrm{linear} \\ $$$${y}={kx}+{d}\:\Leftrightarrow\:{P}=\begin{pmatrix}{{x}}\\{{kx}+{d}}\end{pmatrix}\:\rightarrow\:{P}'=\begin{pmatrix}{{x}}\\{\frac{{b}}{{a}}\left({kx}+{d}\right)}\end{pmatrix}\:\Leftrightarrow\:{y}=\frac{{bk}}{{a}}{x}+\frac{{bd}}{{a}} \\ $$$$\mathrm{straight}\:\mathrm{lines}\:\mathrm{stay}\:\mathrm{straight}\:\mathrm{lines} \\ $$

Commented by ajfour last updated on 12/Jan/19

Thanks MjS Sir, i′ll have to practice this concept. Then i can appreciate your solution much more.

$${Thanks}\:{MjS}\:{Sir},\:{i}'{ll}\:{have}\:{to}\:{practice} \\ $$$${this}\:{concept}.\:\:{Then}\:{i}\:{can}\: \\ $$$${appreciate}\:{your}\:{solution}\:{much}\:{more}. \\ $$

Commented by MJS last updated on 12/Jan/19

anyway this doesn′t lead to the smallest possible perimeter... ellipses are strange figures

$$\mathrm{anyway}\:\mathrm{this}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{the}\:\mathrm{smallest} \\ $$$$\mathrm{possible}\:\mathrm{perimeter}...\:\mathrm{ellipses}\:\mathrm{are}\:\mathrm{strange} \\ $$$$\mathrm{figures} \\ $$

Commented by ajfour last updated on 12/Jan/19

do you mean some other orientation then shall give minimum perimeter, other than the two shown in question?

$${do}\:{you}\:{mean}\:{some}\:{other}\:{orientation} \\ $$$${then}\:{shall}\:{give}\:{minimum}\:{perimeter}, \\ $$$${other}\:{than}\:{the}\:{two}\:{shown}\:{in}\:{question}? \\ $$

Commented by MJS last updated on 12/Jan/19

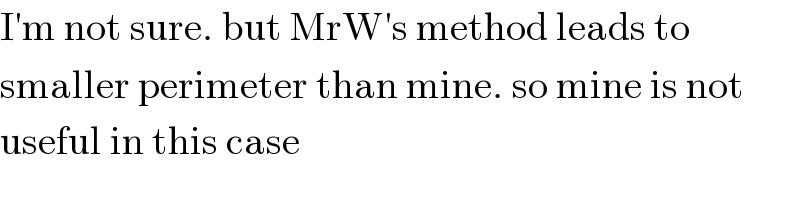
I′m not sure. but MrW′s method leads to smaller perimeter than mine. so mine is not useful in this case

$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}.\:\mathrm{but}\:\mathrm{MrW}'\mathrm{s}\:\mathrm{method}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{smaller}\:\mathrm{perimeter}\:\mathrm{than}\:\mathrm{mine}.\:\mathrm{so}\:\mathrm{mine}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{useful}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$

Commented by ajfour last updated on 26/Jan/19

this might be required again in this trapezium problem..thought of reviewing it!

$${this}\:{might}\:{be}\:{required}\:{again}\:{in}\:{this} \\ $$$${trapezium}\:{problem}..{thought}\:{of} \\ $$$${reviewing}\:{it}! \\ $$

Answered by mr W last updated on 12/Jan/19

let μ=(a/b) let ∠RPQ=θ, (1/t)=tan θ Q(0,h) eqn. of PQ: (x/t)+y=h due to tangency: (a^2 /t^2 )+b^2 =h^2 ⇒h=(b/t)(√(μ^2 +t^2 )) RP=2(b+h)(1/(tan θ))=2(b+h)t QP=(b+h)(1/(sin θ))=(b+h)(√(1+t^2 )) perimeter U=RP+2QP U=2(b+h)(t+(√(1+t^2 ))) U=2b[1+(√(1+((μ/t))^2 ))](t+(√(1+t^2 ))) (U/(2b))=f(t)=[1+(√(1+((μ/t))^2 ))](t+(√(1+t^2 ))) f′(t)=((2((μ/t))(−(μ/t^2 )))/(2(√(1+((μ/t))^2 ))))(t+(√(1+t^2 )))+[1+(√(1+((μ/t))^2 ))](1+((2t)/(2(√(1+t^2 )))))=0 (μ^2 /(t^3 (√(1+((μ/t))^2 ))))=[1+(√(1+((μ/t))^2 ))]((1/(√(1+t^2 )))) μ^2 (√(1+t^2 ))=t^3 [1+(μ^2 /t^2 )+(√(1+((μ/t))^2 ))] ⇒μ^2 ((√(1+t^2 ))−t)=t^2 (t+(√(μ^2 +t^2 ))) ⇒solve for t=t(μ)... example μ=(a/b)=2: ⇒t=0.8045⇒f(t)=7.6828⇒U=15.3656b with orientation 2: μ=(1/2) ⇒t=0.4022⇒f(t)=3.8414⇒U=7.6828a=15.3656b i.e. both orientations give the same miminum perimeter. RP=2b[1+(√(1+((μ/t))^2 ))]t=5.92b PQ=RQ=b[1+(√(1+((μ/t))^2 ))](√(1+t^2 ))=4.72b

$${let}\:\mu=\frac{{a}}{{b}} \\ $$$${let}\:\angle{RPQ}=\theta,\:\frac{\mathrm{1}}{{t}}=\mathrm{tan}\:\theta \\ $$$${Q}\left(\mathrm{0},{h}\right) \\ $$$${eqn}.\:{of}\:{PQ}: \\ $$$$\frac{{x}}{{t}}+{y}={h} \\ $$$${due}\:{to}\:{tangency}: \\ $$$$\frac{{a}^{\mathrm{2}} }{{t}^{\mathrm{2}} }+{b}^{\mathrm{2}} ={h}^{\mathrm{2}} \\ $$$$\Rightarrow{h}=\frac{{b}}{{t}}\sqrt{\mu^{\mathrm{2}} +{t}^{\mathrm{2}} } \\ $$$${RP}=\mathrm{2}\left({b}+{h}\right)\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\mathrm{2}\left({b}+{h}\right){t} \\ $$$${QP}=\left({b}+{h}\right)\frac{\mathrm{1}}{\mathrm{sin}\:\theta}=\left({b}+{h}\right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${perimeter}\:{U}={RP}+\mathrm{2}{QP} \\ $$$${U}=\mathrm{2}\left({b}+{h}\right)\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$${U}=\mathrm{2}{b}\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\frac{{U}}{\mathrm{2}{b}}={f}\left({t}\right)=\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$${f}'\left({t}\right)=\frac{\mathrm{2}\left(\frac{\mu}{{t}}\right)\left(−\frac{\mu}{{t}^{\mathrm{2}} }\right)}{\mathrm{2}\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)+\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{2}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)=\mathrm{0} \\ $$$$\frac{\mu^{\mathrm{2}} }{{t}^{\mathrm{3}} \sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }}=\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]\left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right) \\ $$$$\mu^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }={t}^{\mathrm{3}} \left[\mathrm{1}+\frac{\mu^{\mathrm{2}} }{{t}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow\mu^{\mathrm{2}} \left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−{t}\right)={t}^{\mathrm{2}} \left({t}+\sqrt{\mu^{\mathrm{2}} +{t}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{solve}\:{for}\:{t}={t}\left(\mu\right)... \\ $$$$ \\ $$$${example}\:\mu=\frac{{a}}{{b}}=\mathrm{2}: \\ $$$$\Rightarrow{t}=\mathrm{0}.\mathrm{8045}\Rightarrow{f}\left({t}\right)=\mathrm{7}.\mathrm{6828}\Rightarrow{U}=\mathrm{15}.\mathrm{3656}{b} \\ $$$$ \\ $$$${with}\:{orientation}\:\mathrm{2}:\:\mu=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{t}=\mathrm{0}.\mathrm{4022}\Rightarrow{f}\left({t}\right)=\mathrm{3}.\mathrm{8414}\Rightarrow{U}=\mathrm{7}.\mathrm{6828}{a}=\mathrm{15}.\mathrm{3656}{b} \\ $$$$ \\ $$$${i}.{e}.\:{both}\:{orientations}\:{give}\:{the}\:{same} \\ $$$${miminum}\:{perimeter}. \\ $$$${RP}=\mathrm{2}{b}\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]{t}=\mathrm{5}.\mathrm{92}{b} \\ $$$${PQ}={RQ}={b}\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\frac{\mu}{{t}}\right)^{\mathrm{2}} }\right]\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{4}.\mathrm{72}{b} \\ $$

Commented by ajfour last updated on 12/Jan/19

Very Nice! Understood Sir, i had to go along writing it.

$$\mathcal{V}{ery}\:\mathcal{N}{ice}!\:{Understood}\:{Sir},\:{i}\:{had}\:{to} \\ $$$${go}\:{along}\:{writing}\:{it}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com