Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 52841 by Tawa1 last updated on 13/Jan/19

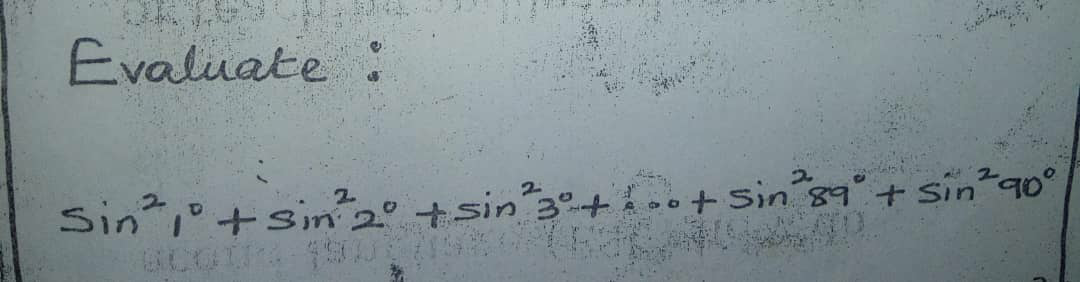
Commented by maxmathsup by imad last updated on 14/Jan/19

$$\pi \to {180}^o$$$$\alpha \to k^o\Rightarrow {180}^{}.\alpha =k\pi \Rightarrow \alpha =\frac{k\pi }{180}\Rightarrow$$$$S=\sum _{k=0}^{90}{sin}^2\left(\frac{k\pi }{180}\right)generallyletdetermine{S}_n=\sum _{k=0}^n{sin}^2\left(\frac{k\pi }{180}\right)\Rightarrow$$$$S_n=\sum _{k=0}^n\frac{1-cos\left(\frac{k\pi }{90}\right)}{2}=\frac{n+1}{2}-\frac{1}{2}\sum _{k=0}^{n}cos\left(\frac{k\pi }{90}\right)but$$$$\sum _{k=0}^{n}cos\left(\frac{k\pi }{90}\right)=Re\left(\sum _{k=0}^n{e}^{i\frac{k\pi }{90}}\right)and\sum _{k=0}^n{e}^{i\frac{k\pi }{90}}=\sum _{k=0}^n{\left(e^{\frac{i\pi }{90}}\right)}^k$$$$=\frac{1-e^{i(n+1)\frac{\pi }{90}}}{1-e^{\frac{i\pi }{90}}}=\frac{1-cos\left(\frac{(n+1)\pi }{90}\right)-isin\left(\frac{(n+1)\pi }{90}\right)}{1-cos\left(\frac{\pi }{90}\right)-isin\left(\frac{\pi }{90}\right)}$$$$=\frac{2{sin}^2\left(\frac{(n+1)\pi }{180}\right)-2isin\left(\frac{(n+1)\pi }{180}\right)cos\left(\frac{(n+1)\pi }{180}\right)}{2{sin}^2\left(\frac{\pi }{180}\right)-2isin\left(\frac{\pi }{180}\right)cos\left(\frac{\pi }{180}\right)}$$$$=\frac{-isin\left(\frac{(n+1)\pi }{180}\right)\left(e^{i\frac{(n+1)\pi }{180}}\right)}{-isin\left(\frac{\pi }{180}\right)e^{\frac{i\pi }{180}}}=\frac{sin\left(\frac{(n+1)\pi }{180}\right)}{sin\left(\frac{\pi }{180}\right)}{e}^{\frac{in\pi }{180}}\Rightarrow$$$$\sum _{k=0}^{n}cos\left(\frac{k\pi }{90}\right)=\frac{sin\left(\frac{(n+1)\pi }{180}\right)cos\left(\frac{n\pi }{180}\right)}{sin\left(\frac{\pi }{180}\right)}\Rightarrow$$$$S_n=\frac{n+1}{2}-\frac{sin\left(\frac{(n+1)\pi }{180}\right)cos\left(\frac{n\pi }{180}\right)}{sin\left(\frac{\pi }{180}\right)}\Rightarrow S=S_{90}=\frac{91}{2}-\frac{sin\left(\frac{91\pi }{180}\right)cos\left(\frac{\pi }{2}\right)}{sin\left(\frac{\pi }{180}\right)}$$$$=\frac{91}{2}-0\Rightarrow S=\frac{91}{2}.$$$$$$

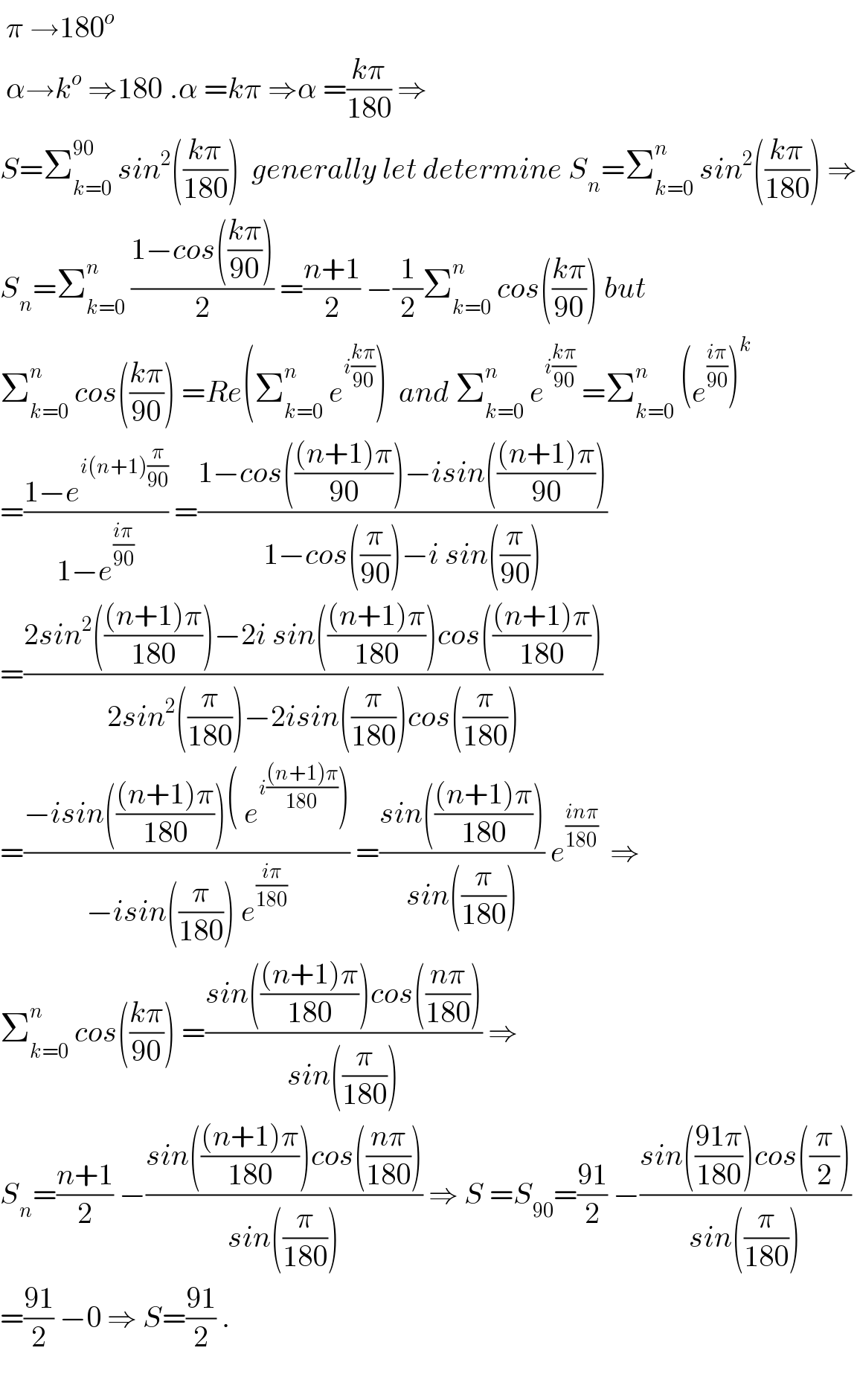
Commented by Tawa1 last updated on 16/Jan/19

$$\mathrm{God}\mathrm{bless}\mathrm{you}\mathrm{sir}$$

Commented by Tawa1 last updated on 17/Jan/19

$$\mathrm{Sir},\mathrm{please}\mathrm{explain}\mathrm{from}\mathrm{here}\mathrm{sir}.$$$$\mathrm{How}{\mathrm{S}}_{\mathrm{n}}=\sum _{\mathrm{k}=0}^{\mathrm{n}}{\sin }^2\left(\frac{\mathrm{k}\pi }{180}\right)\mathrm{becomes}$$$${\mathrm{S}}_{\mathrm{n}}=\sum _{\mathrm{k}=0}^{\mathrm{n}}\frac{1-\cos \left(\frac{\mathrm{k}\pi }{90}\right)}{2}=\frac{\mathrm{n}+1}{2}-\frac{1}{2}\sum _{\mathrm{k}=0}^{\mathrm{n}}\cos \left(\frac{\mathrm{k}\pi }{90}\right)$$$$$$$$\mathrm{And}\mathrm{how}2\mathrm{becomes}1-{\mathrm{e}}^{\mathrm{i}\frac{\pi }{90}}$$$$\mathrm{please}\mathrm{sir}.$$

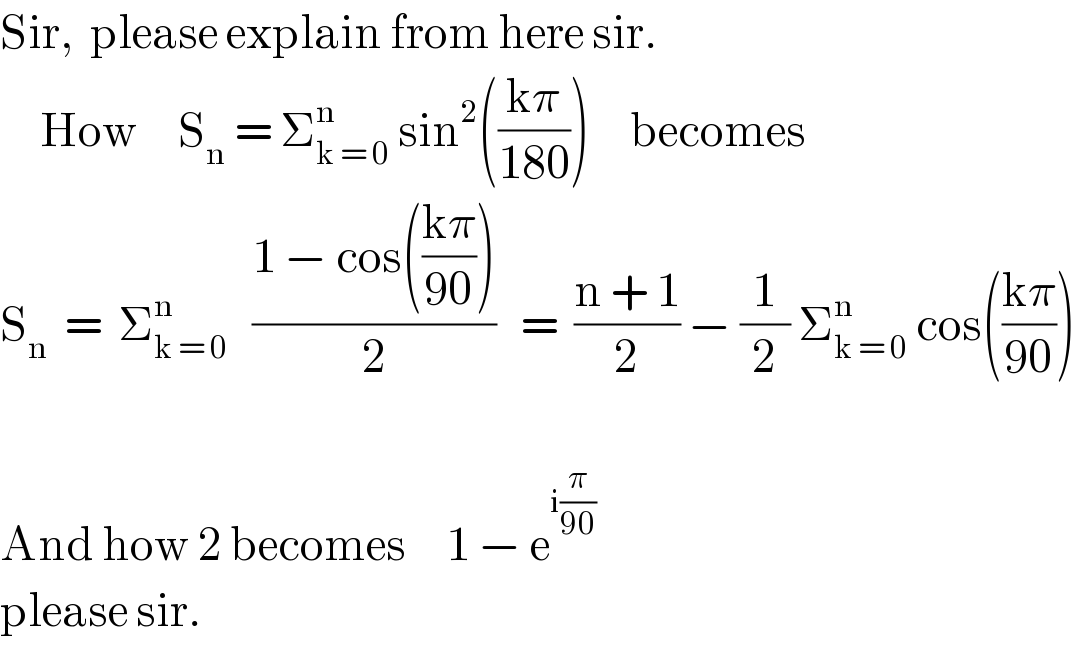
Commented by maxmathsup by imad last updated on 19/Jan/19

$$sirtakex=\frac{k\pi }{180}anduseformulalae{sin}^2\left(x\right)=\frac{1-cos\left(2x\right)}{2}$$$$also\sum _{k=0}^n\frac{1-cos\left(\frac{k\pi }{90}\right)}{2}=\frac{1}{2}\sum _{k=0}^n\left(1\right)-\frac{1}{2}\sum _{k=0}^{n}cos\left(\frac{k\pi }{90}\right)and$$$$\sum _{k=0}^n\left(1\right)=n+1(lookthat\sum _{k=0}^{n}a=(n+1)a)$$

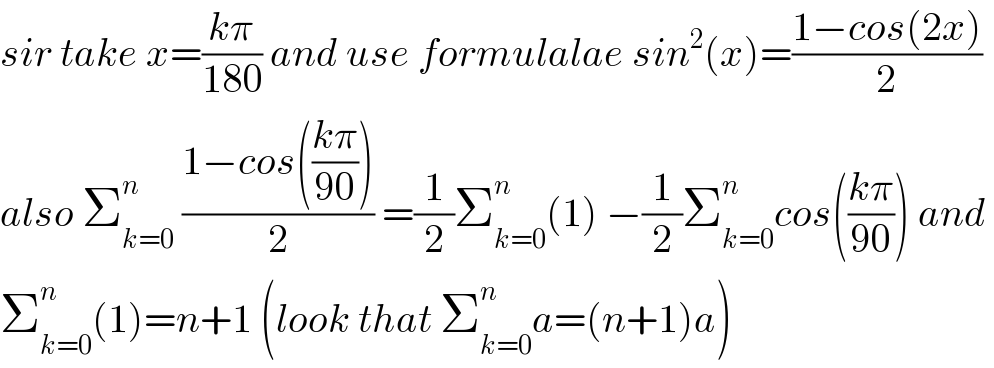
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19

$$1+89=90so{sin}^{2}1+{sin}^{2}89$$$$={sin}^{2}1+{sin}^2(90-1)$$$$={sin}^{2}1+{cos}^{2}1$$$$=1$$$$similarly..$$$$2+88=90$$$$...$$$$...$$$$45+45=90$$$$$$$$s=({sin}^{2}1+{sin}^{2}2+{sin}^{2}3+...+{sin}^{2}89)+{sin}^{2}90$$$$s=({sin}^{2}89+{sin}^{2}88+{sin}^{2}87+..+{sin}^{2}1)+{sin}^{2}90$$$$2s=[({sin}^{2}1+{sin}^{2}89)+({sin}^{2}2+{sin}^{2}88)+..+({sin}^{2}89+{sin}^{2}1)]+(1+1)$$$$2s=[1+1+1...89times]+2$$$$s=\frac{91}{2}=45.5$$$$$$

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19

$$thankyou..Godblessall...$$

Commented by Tawa1 last updated on 14/Jan/19

$$\mathrm{God}\mathrm{bless}\mathrm{you}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com