
Question and Answers Forum
Question Number 53066 by ajfour last updated on 16/Jan/19

Commented by ajfour last updated on 17/Jan/19
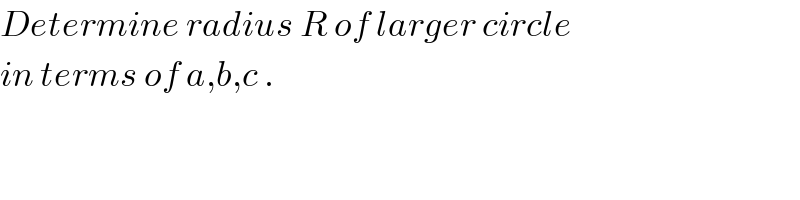
Commented by ajfour last updated on 17/Jan/19

Commented by MJS last updated on 17/Jan/19

Commented by ajfour last updated on 18/Jan/19

Commented by ajfour last updated on 18/Jan/19
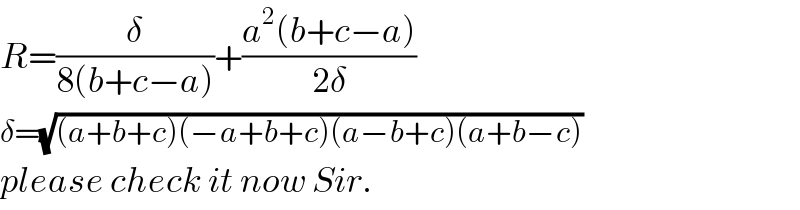
Commented by ajfour last updated on 18/Jan/19
![BK = R, BM=(a/2) ⇒ MK=(√(R^2 −(a^2 /4))) JN = r−(√(R^2 −(a^2 /4))) , KN = R−r Now r(cot θ+cot φ)=a r(cot θ+cot ψ)=c r(cot φ+cot ψ)=b ⇒ 2rcot θ = a+c−b rcot θ = ((c−b)/2)+(a/2) BP = rcot θ JK = MP = BP−(a/2) JK = rcot θ−(a/2) = ((c−b)/2) In △JKN KN^( 2) =JK^( 2) +JN^( 2) ⇒ (R−r)^2 =(((c−b)/2))^2 +(r−(√(R^2 −(a^2 /4))))^2 ⇒ R^2 −2rR+r^2 =(((c−b)/2))^2 +r^2 +R^2 −(a^2 /4) −2r(√(R^2 −(a^2 /4))) ⇒ 2r(R−(√(R^2 −(a^2 /4))))=(((a+c−b)(a+b−c))/4) let area(△ABC)=△ we know r(a+b+c)= 2△ , and △= (√(s(s−a)(s−b)(s−c))) If δ=(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) ⇒ 4△= δ = 2r(a+b+c) ⇒ r = (𝛅/(2(a+b+c))) 2r(R−(√(R^2 −(a^2 /4))))=(((a+c−b)(a+b−c))/4) gives 2r(R−(√(R^2 −(a^2 /4))) ) = (δ^2 /(4(a+b+c)(b+c−a))) ⇒ R−(√(R^2 −(a^2 /4))) = (δ/(4(b+c−a))) ⇒ R^2 −(a^2 /4)=[R−(δ/(4(b+c−a)))]^2 ⇒ ((Rδ)/(2(b+c−a)))=(a^2 /4)+(δ^2 /(16(b+c−a)^2 )) ⇒ R=((a^2 (b+c−a))/(2δ))+(δ/(8(b+c−a))) .](Q53123.png)
Commented by MJS last updated on 18/Jan/19

Commented by MJS last updated on 18/Jan/19

Commented by behi83417@gmail.com last updated on 19/Jan/19

Answered by MJS last updated on 18/Jan/19

Commented by MJS last updated on 18/Jan/19
Commented by ajfour last updated on 18/Jan/19
Commented by mr W last updated on 18/Jan/19
Commented by ajfour last updated on 18/Jan/19

