Question Number 53071 by behi83417@gmail.com last updated on 16/Jan/19
Commented by behi83417@gmail.com last updated on 16/Jan/19
$${as}\:{shown}\:{in}\:{fig}: \\ $$$${prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\rightarrow\:\frac{\boldsymbol{\mathrm{area}}\:\boldsymbol{\mathrm{of}}\:\:{outer}\:\:\boldsymbol{\mathrm{hexagon}}}{\boldsymbol{\mathrm{area}}\:\boldsymbol{\mathrm{of}}\:\:{inner}\:\boldsymbol{\mathrm{triangle}}}\:\:\:\geqslant\:\mathrm{13} \\ $$
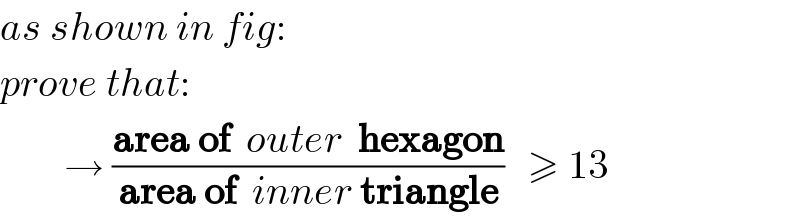
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
![area ABC triangle=S S=(1/2)acsinB=(1/2)absinC=(1/2)bcsinA others three triangle ...butterfly wings like.. are also S. area of hexagon=4S+P+Q+R now S+Q=(1/2)(b+c)(a+b)sinB S+P=(1/2)(a+c)(a+b)sinA S+R=(1/2)(b+c)(a+c)sinC now we know ((sinA)/a)=((sinB)/b)=((sinC)/c)=k(say) so △ABC area=(1/2)acsinB=((abck)/2) area hexagon=4S+P+Q+R =(S+P)+(S+Q)+(S+R)+S =(((a+c)(a+b)ka+(b+c)(a+b)kb+(b+c)(a+c)kc+abck)/2) =(k/2)[(a^2 +ab+ac+bc)a+(ab+b^2 +ac+bc)b+(ab+bc+ac+c^2 )c+abc] =(k/2)[a^3 +a^2 b+a^2 c+abc+ab^2 +b^3 +abc+b^2 c+abc+bc^2 +ac^2 +c^3 +abc] =(k/2)[4abc+a^3 +b^3 +c^3 +a^2 (b+c)+b^2 (a+c)+c^2 (a+b)] =2abck+(k/2)[a^2 (a+b+c)+b^2 (a+b+c)+c^2 (a+b+c)] =2abck+(k/2)[(a+b+c)(a^2 +b^2 +c^2 )] now ((a+b+c)/3)≥(abc)^(1/3) ((a^2 +b^2 +c^2 )/3)≥(a^2 b^2 c^2 )^(1/3) so(a+b+c)(a^2 +b^2 +c^2 )≥9abc so area of hexagon =2abck+(k/2)(a+b+c)(a^2 +b^2 +c^2 )≥2abck+((9abck)/2) so area of hexagon≥((13abck)/2) area of hexagon≥13×area of △ABC ((area of hexagon)/(△ABC))≥13 proved](Q53095.png)
$${area}\:{ABC}\:{triangle}={S} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}{acsinB}=\frac{\mathrm{1}}{\mathrm{2}}{absinC}=\frac{\mathrm{1}}{\mathrm{2}}{bcsinA} \\ $$$${others}\:{three}\:{triangle}\:...\boldsymbol{{butterfly}}\:\boldsymbol{{wings}}\:\boldsymbol{{like}}.. \\ $$$$\boldsymbol{{are}}\:\boldsymbol{{also}}\:\boldsymbol{{S}}. \\ $$$${area}\:{of}\:{hexagon}=\mathrm{4}{S}+{P}+{Q}+{R} \\ $$$${now}\:{S}+{Q}=\frac{\mathrm{1}}{\mathrm{2}}\left({b}+{c}\right)\left({a}+{b}\right){sinB} \\ $$$${S}+{P}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{c}\right)\left({a}+{b}\right){sinA} \\ $$$${S}+{R}=\frac{\mathrm{1}}{\mathrm{2}}\left({b}+{c}\right)\left({a}+{c}\right){sinC} \\ $$$${now}\:{we}\:{know} \\ $$$$\frac{{sinA}}{{a}}=\frac{{sinB}}{{b}}=\frac{{sinC}}{{c}}={k}\left({say}\right) \\ $$$${so}\:\bigtriangleup{ABC}\:{area}=\frac{\mathrm{1}}{\mathrm{2}}{acsinB}=\frac{{abck}}{\mathrm{2}} \\ $$$${area}\:{hexagon}=\mathrm{4}{S}+{P}+{Q}+{R} \\ $$$$=\left({S}+{P}\right)+\left({S}+{Q}\right)+\left({S}+{R}\right)+{S} \\ $$$$=\frac{\left({a}+{c}\right)\left({a}+{b}\right){ka}+\left({b}+{c}\right)\left({a}+{b}\right){kb}+\left({b}+{c}\right)\left({a}+{c}\right){kc}+{abck}}{\mathrm{2}} \\ $$$$=\frac{{k}}{\mathrm{2}}\left[\left({a}^{\mathrm{2}} +{ab}+{ac}+{bc}\right){a}+\left({ab}+{b}^{\mathrm{2}} +{ac}+{bc}\right){b}+\left({ab}+{bc}+{ac}+{c}^{\mathrm{2}} \right){c}+{abc}\right] \\ $$$$=\frac{{k}}{\mathrm{2}}\left[{a}^{\mathrm{3}} +{a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} {c}+{abc}+{ab}^{\mathrm{2}} +{b}^{\mathrm{3}} +{abc}+{b}^{\mathrm{2}} {c}+{abc}+{bc}^{\mathrm{2}} +{ac}^{\mathrm{2}} +{c}^{\mathrm{3}} +{abc}\right] \\ $$$$=\frac{{k}}{\mathrm{2}}\left[\mathrm{4}{abc}+{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +{a}^{\mathrm{2}} \left({b}+{c}\right)+{b}^{\mathrm{2}} \left({a}+{c}\right)+{c}^{\mathrm{2}} \left({a}+{b}\right)\right] \\ $$$$=\mathrm{2}{abck}+\frac{{k}}{\mathrm{2}}\left[{a}^{\mathrm{2}} \left({a}+{b}+{c}\right)+{b}^{\mathrm{2}} \left({a}+{b}+{c}\right)+{c}^{\mathrm{2}} \left({a}+{b}+{c}\right)\right] \\ $$$$\:\:=\mathrm{2}{abck}+\frac{{k}}{\mathrm{2}}\left[\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\right] \\ $$$${now}\:\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}\geqslant\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${so}\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\geqslant\mathrm{9}{abc} \\ $$$${so}\:{area}\:{of}\:{hexagon} \\ $$$$=\mathrm{2}{abck}+\frac{{k}}{\mathrm{2}}\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\geqslant\mathrm{2}{abck}+\frac{\mathrm{9}{abck}}{\mathrm{2}} \\ $$$${so}\:{area}\:{of}\:{hexagon}\geqslant\frac{\mathrm{13}{abck}}{\mathrm{2}} \\ $$$${area}\:{of}\:{hexagon}\geqslant\mathrm{13}×{area}\:{of}\:\bigtriangleup{ABC} \\ $$$$\frac{{area}\:{of}\:{hexagon}}{\bigtriangleup{ABC}}\geqslant\mathrm{13}\:{proved} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
$${sir}\:{pls}\:{check}\:{i}\:{have}\:{proved}... \\ $$
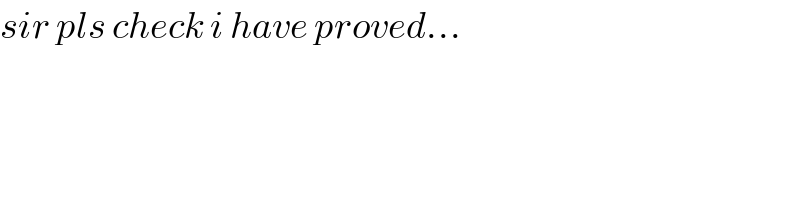
Commented by behi83417@gmail.com last updated on 17/Jan/19
$${thank}\:{you}\:{very}\:{much}\:{sir}\:{tanmay}. \\ $$$${it}\:{is}\:{a}\:{nice}\:{and}\:{smart}\:{work}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
$${thank}\:{you}\:{sir}... \\ $$