
Question Number 532 by 123456 last updated on 25/Jan/15

$${if}\:{f}\:{is}\:{continuos}\:{and}\:{diferentiable} \\ $$$${everywhere}\:{on}\:\mathbb{R},\:{if}\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:{and} \\ $$$$\mid{f}'\left({x}\right)\mid\leqslant\mid{f}\left({x}\right)\mid\:{then}\:{proof}\:{that} \\ $$$${f}\left({x}\right)=\mathrm{0} \\ $$
Answered by prakash jain last updated on 06/Feb/15
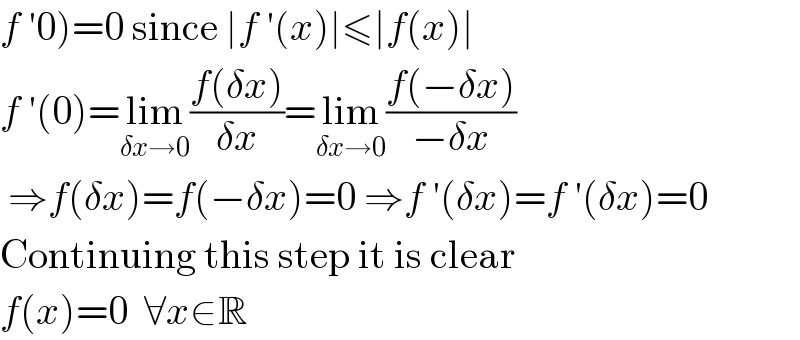
$$\left.{f}\:'\mathrm{0}\right)=\mathrm{0}\:\mathrm{since}\:\mid{f}\:'\left({x}\right)\mid\leqslant\mid{f}\left({x}\right)\mid \\ $$$${f}\:'\left(\mathrm{0}\right)=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\delta{x}\right)}{\delta{x}}=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(−\delta{x}\right)}{−\delta{x}} \\ $$$$\:\Rightarrow{f}\left(\delta{x}\right)={f}\left(−\delta{x}\right)=\mathrm{0}\:\Rightarrow{f}\:'\left(\delta{x}\right)={f}\:'\left(\delta{x}\right)=\mathrm{0} \\ $$$$\mathrm{Continuing}\:\mathrm{this}\:\mathrm{step}\:\mathrm{it}\:\mathrm{is}\:\mathrm{clear} \\ $$$${f}\left({x}\right)=\mathrm{0}\:\:\forall{x}\in\mathbb{R} \\ $$
