
Question and Answers Forum
Question Number 53228 by maxmathsup by imad last updated on 19/Jan/19
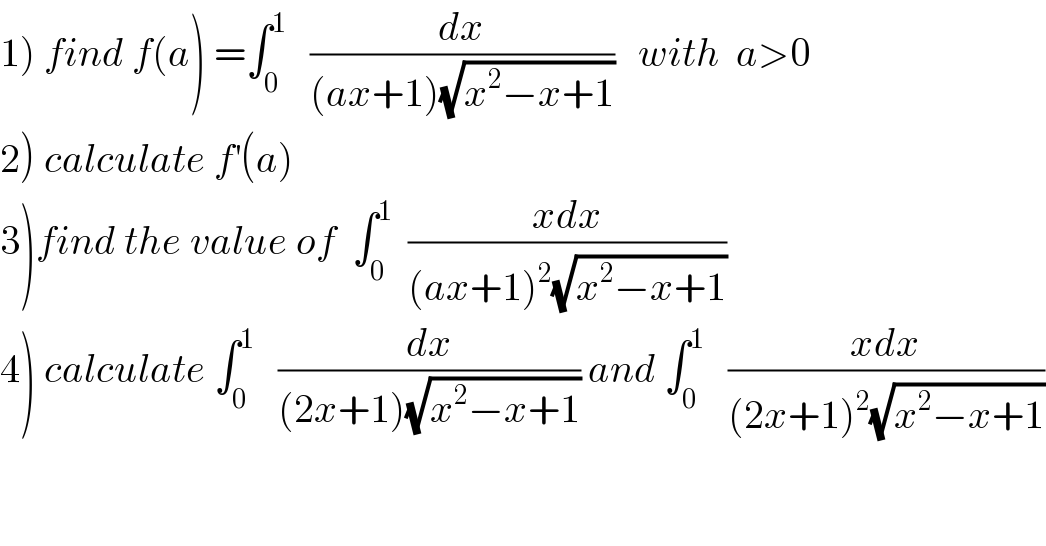
Commented byAbdo msup. last updated on 20/Jan/19
![1)we have x^2 −x +1 =(x−(1/2))^2 +(3/4) changement x−(1/2) =((√3)/2)sh(t) give f(a) = ∫_(argsh(−(1/(√3)))) ^(argsh((1/(√3)))) (1/((a((1/2)+((√3)/2)sh(t))+1)((√3)/2)ch(t)))((√3)/2)ch(t)dt =∫_(ln(−(1/(√3)) +(2/(√3)))) ^(ln((1/(√3)) +(2/(√3)))) ((2dt)/(a +a(√3)sh(t)+2)) =∫_(ln((1/(√3)))) ^(ln((√3))) ((2dt)/(a+a(√3)((e^t −e^(−t) )/2)+2)) = 4 ∫_(ln((1/(√3)))) ^(ln((√3))) (dt/(2a +a(√3)(e^t −e^(−t) )+4)) =_(e^t =u) 4 ∫_(1/(√3)) ^(√3) (1/(2a+a(√3)(u−u^(−1) )+4)) (du/u) =4 ∫_(1/(√3)) ^(√3) (du/(2au +a(√3)u^2 −a(√3) +4u)) =4 ∫_(1/(√3)) ^(√3) (du/(a(√3)u^2 +(2a+4)u−a(√3))) roots of p(u)=a(√3)u^2 +(2a+4)u−a(√3) Δ^′ =(a+2)^2 +3a^2 =a^2 +4a +4 +3a^2 =4a^2 +4a + u_1 =((−a−2+2(√(1+a+a^2 )))/(a(√3))) u_2 =((−a−2−2(√(1+a+a^2 )))/(a(√3))) ⇒ F(u) =(1/(a(√3)(u−u_1 )(u−u_2 ))) =(1/(a(√3)))(1/(u_1 −u_2 )){ (1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(a(√3))) (1/((4(√(1+a+a^2 )))/(a(√3)))) {(1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(4(√(1+a+a^2 )))){(1/(u−u_1 )) −(1/(u−u_2 ))}? ⇒ f(a) =(1/(√(1+a+a^2 ))) [ln∣((u−u_1 )/(u−u_2 ))∣]_(1/(√3)) ^(√3) =(1/(√(1+a+a^2 ))){ln∣(((√3)−u_1 )/((√3)−u_2 ))∣−ln∣(((1/(√3))−u_1 )/((1/(√3))−u_2 ))∣} =(1/(√(1+a+a^2 ))){ln∣(((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3))))/((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3)))))∣ −ln∣((1−(√3)((−a−2+2(√(1+a+a^2 )))/(a(√3))))/(1−(√3)((−a−2 −2(√(1+a+a^2 )))/(a(√3)))))∣ =(1/(√(1+a+a^2 ))){ ln∣((4a+2+2(√(1+a+a^2 )))/(4a+2−2(√(1+a+a^2 ))))∣ −ln∣ ((2a(√3)+2−2(√(1+a+a^2 )))/(2a(√3)+2 +2(√(1+a+a^2 ))))∣} ⇒f(a) =(1/(√(1+a+a^2 ))){ ln∣((2a+1+(√(1+a+a^2 )))/(2a+1−(√(1+a+a^2 ))))∣ −ln∣((a(√3)+1−(√(1+a+a^2 )))/(a(√3)+1 +(√(1+a+a^2 ))))∣} .](Q53320.png)
Commented byAbdo msup. last updated on 20/Jan/19

Commented byAbdo msup. last updated on 20/Jan/19
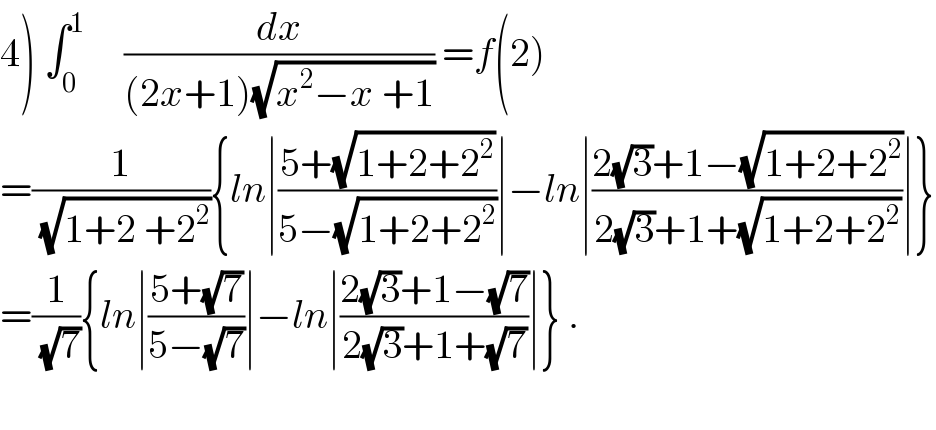
| ||
Question and Answers Forum | ||
Question Number 53228 by maxmathsup by imad last updated on 19/Jan/19 | ||
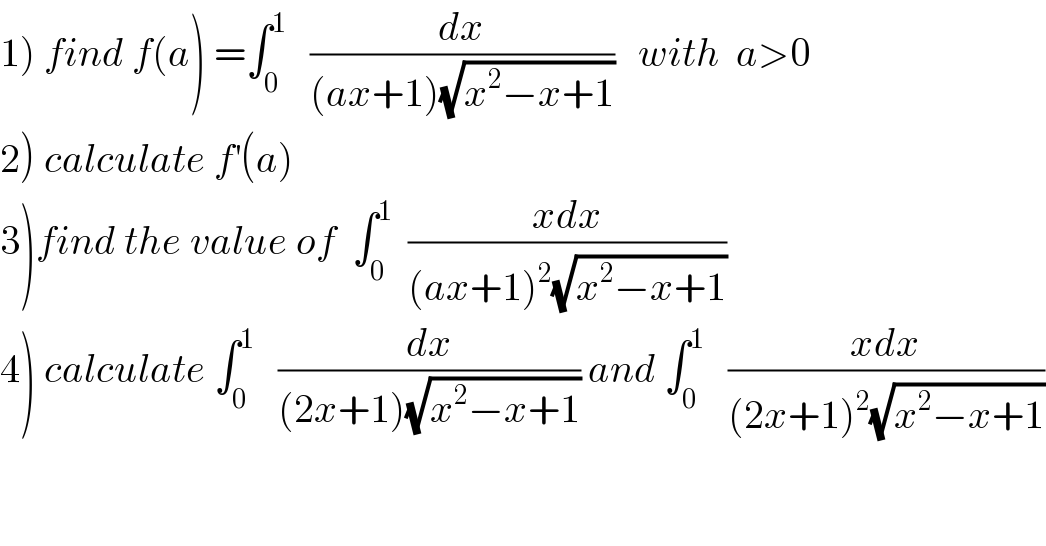 | ||
Commented byAbdo msup. last updated on 20/Jan/19 | ||
![1)we have x^2 −x +1 =(x−(1/2))^2 +(3/4) changement x−(1/2) =((√3)/2)sh(t) give f(a) = ∫_(argsh(−(1/(√3)))) ^(argsh((1/(√3)))) (1/((a((1/2)+((√3)/2)sh(t))+1)((√3)/2)ch(t)))((√3)/2)ch(t)dt =∫_(ln(−(1/(√3)) +(2/(√3)))) ^(ln((1/(√3)) +(2/(√3)))) ((2dt)/(a +a(√3)sh(t)+2)) =∫_(ln((1/(√3)))) ^(ln((√3))) ((2dt)/(a+a(√3)((e^t −e^(−t) )/2)+2)) = 4 ∫_(ln((1/(√3)))) ^(ln((√3))) (dt/(2a +a(√3)(e^t −e^(−t) )+4)) =_(e^t =u) 4 ∫_(1/(√3)) ^(√3) (1/(2a+a(√3)(u−u^(−1) )+4)) (du/u) =4 ∫_(1/(√3)) ^(√3) (du/(2au +a(√3)u^2 −a(√3) +4u)) =4 ∫_(1/(√3)) ^(√3) (du/(a(√3)u^2 +(2a+4)u−a(√3))) roots of p(u)=a(√3)u^2 +(2a+4)u−a(√3) Δ^′ =(a+2)^2 +3a^2 =a^2 +4a +4 +3a^2 =4a^2 +4a + u_1 =((−a−2+2(√(1+a+a^2 )))/(a(√3))) u_2 =((−a−2−2(√(1+a+a^2 )))/(a(√3))) ⇒ F(u) =(1/(a(√3)(u−u_1 )(u−u_2 ))) =(1/(a(√3)))(1/(u_1 −u_2 )){ (1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(a(√3))) (1/((4(√(1+a+a^2 )))/(a(√3)))) {(1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(4(√(1+a+a^2 )))){(1/(u−u_1 )) −(1/(u−u_2 ))}? ⇒ f(a) =(1/(√(1+a+a^2 ))) [ln∣((u−u_1 )/(u−u_2 ))∣]_(1/(√3)) ^(√3) =(1/(√(1+a+a^2 ))){ln∣(((√3)−u_1 )/((√3)−u_2 ))∣−ln∣(((1/(√3))−u_1 )/((1/(√3))−u_2 ))∣} =(1/(√(1+a+a^2 ))){ln∣(((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3))))/((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3)))))∣ −ln∣((1−(√3)((−a−2+2(√(1+a+a^2 )))/(a(√3))))/(1−(√3)((−a−2 −2(√(1+a+a^2 )))/(a(√3)))))∣ =(1/(√(1+a+a^2 ))){ ln∣((4a+2+2(√(1+a+a^2 )))/(4a+2−2(√(1+a+a^2 ))))∣ −ln∣ ((2a(√3)+2−2(√(1+a+a^2 )))/(2a(√3)+2 +2(√(1+a+a^2 ))))∣} ⇒f(a) =(1/(√(1+a+a^2 ))){ ln∣((2a+1+(√(1+a+a^2 )))/(2a+1−(√(1+a+a^2 ))))∣ −ln∣((a(√3)+1−(√(1+a+a^2 )))/(a(√3)+1 +(√(1+a+a^2 ))))∣} .](Q53320.png) | ||
Commented byAbdo msup. last updated on 20/Jan/19 | ||
 | ||
Commented byAbdo msup. last updated on 20/Jan/19 | ||
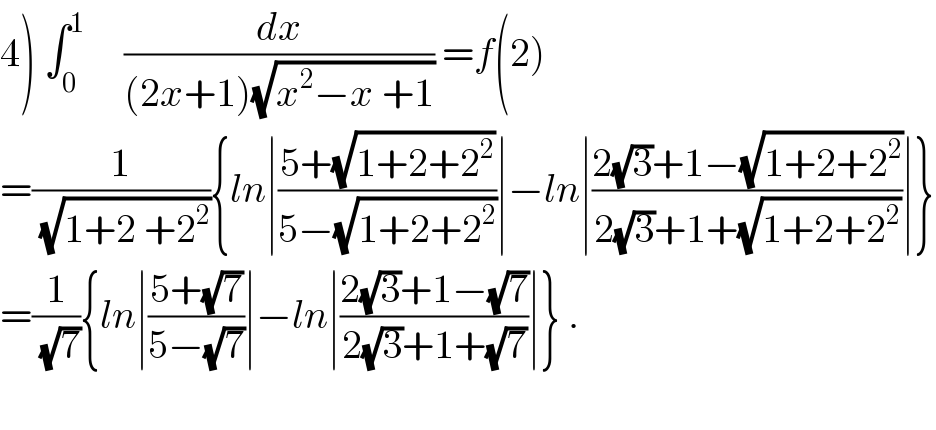 | ||