
Question and Answers Forum
Question Number 100047 by Ar Brandon last updated on 24/Jun/20

Answered by smridha last updated on 24/Jun/20

Commented by Ar Brandon last updated on 24/Jun/20
Thanks, but how do we arrive there ? Or is it just a theory ?
Commented by smridha last updated on 24/Jun/20
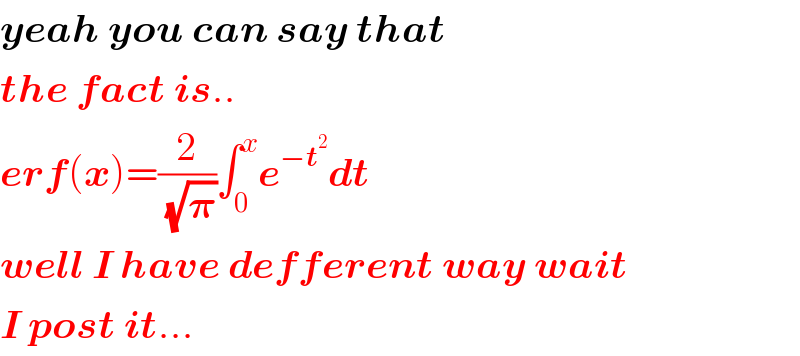
Answered by smridha last updated on 24/Jun/20
![=∫_0 ^1 Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!))dx =1.Σ_(n=0) ^∞ (((−1)^n )/(n!(2n+1))) =Σ_(n=0) ^∞ ((1/2)/((n+(1/2)))).(((−1)^n )/(n!)) =Σ_(n=0 ) ^∞ ((((1/2))_n )/(((3/2))_n )).(((−1)^n )/(n!)) =M((1/2),(3/2),−1)or _1 F_1 ((1/2);(3/2);−1) this is called confluent hypergeometric f^n . note:(a)=(((a)_n )/((a+1)_n ))(a+n)[pochhammer symbol]](Q100060.png)
Commented by Ar Brandon last updated on 24/Jun/20
Thanks so very much��
