Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 53295 by gunawan last updated on 20/Jan/19

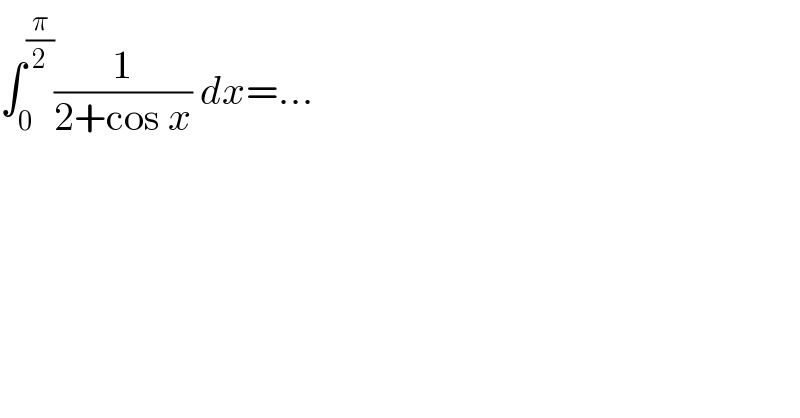
∫_0 ^(π/2) (1/(2+cos x)) dx=...

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+\mathrm{cos}\:{x}}\:{dx}=... \\ $$

Commented by maxmathsup by imad last updated on 20/Jan/19

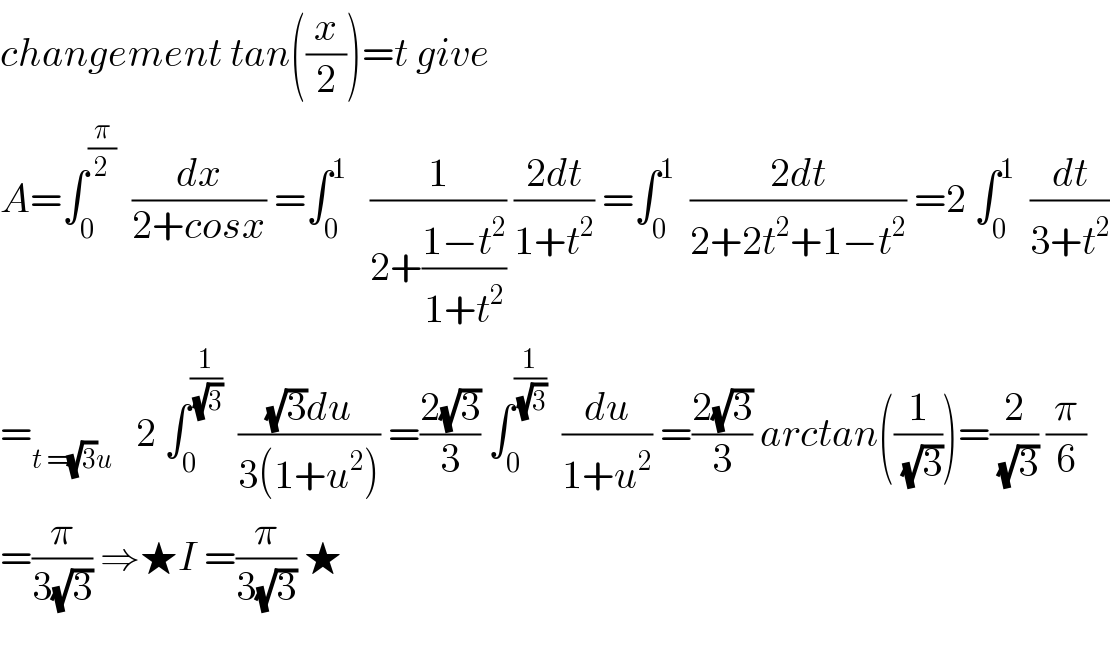
changement tan((x/2))=t give A=∫_0 ^(π/2) (dx/(2+cosx)) =∫_0 ^1 (1/(2+((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^1 ((2dt)/(2+2t^2 +1−t^2 )) =2 ∫_0 ^1 (dt/(3+t^2 )) =_(t =(√3)u) 2 ∫_0 ^(1/(√3)) (((√3)du)/(3(1+u^2 ))) =((2(√3))/3) ∫_0 ^(1/(√3)) (du/(1+u^2 )) =((2(√3))/3) arctan((1/(√3)))=(2/(√3)) (π/6) =(π/(3(√3))) ⇒★I =(π/(3(√3))) ★

$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\: \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{2}+{cosx}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}−{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{3}+{t}^{\mathrm{2}} } \\ $$$$=_{{t}\:=\sqrt{\mathrm{3}}{u}} \:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\frac{\sqrt{\mathrm{3}}{du}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\frac{\pi}{\mathrm{6}} \\ $$$$=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow\bigstar{I}\:=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\bigstar \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19

∫_0 ^(π/2) (1/(2+((1−tan^2 (x/2))/(1+tan^2 (x/2)))))dx ∫_0 ^(π/2) ((sec^2 (x/2))/(2+2tan^2 (x/(2 ))+1−tan^2 (x/2)))dx t=tan(x/2) dt=(1/2)sec^2 (x/2)dx ∫_0 ^1 ((2dt)/(3+t^2 )) 2×(1/(√3))∣tan^(−1) ((t/(√3)))∣_0 ^1 (2/(√3))[tan^(−1) ((1/(√3)))]=(2/(√3))×(π/6)=(π/(3(√3)))

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}+\mathrm{2}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}\:}+\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:\:\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dt}}{\mathrm{3}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}}{\sqrt{\mathrm{3}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{6}}=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Commented by gunawan last updated on 20/Jan/19

thank you Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com