
Question and Answers Forum
Question Number 53463 by maxmathsup by imad last updated on 22/Jan/19
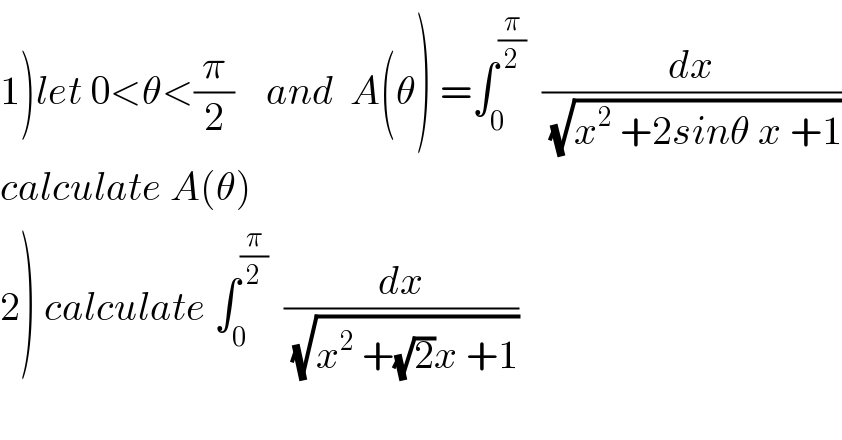
Commented bymaxmathsup by imad last updated on 23/Jan/19
![1) we have A(θ) =∫_0 ^(π/2) (dx/(√(x^2 +2x sinθ +sin^2 θ +cos^2 θ))) =∫_0 ^(π/2) (dx/(√((x+sinθ)^(2 ) +cos^2 θ))) changement x+sinθ=t cosθ give t =((x+sinθ)/(cosθ)) A(θ) = ∫_(tanθ) ^((π/(2cosθ))+tanθ) ((cosθ dt)/(cosθ(√(1+t^2 )))) = ∫_(tanθ) ^((π/(2cosθ)) +tanθ) (dt/(√(1+t^2 ))) =[argsh(t)]_(tanθ) ^((π/(2cosθ))+tanθ) =ln(t+(√(1+t^2 ))]_(tanθ) ^((π/(2cosθ)) +tanθ) = ln((π/(2cosθ)) +tanθ +(√(1+((π/(2cosθ))+tanθ)^2 ))) −ln(tanθ +(√(1+tan^2 θ))) 2) ∫_0 ^(π/2) (dx/(√(x^2 +(√2)x +1))) =A((π/4)) =ln((π/(2 cos((π/4)))) +tan((π/4))+(√(1+((π/(2cos((π/4))))+tan((π/4))^2 )) −ln(tan((π/4))+(√(1+tan^2 ((π/4))))) =ln((π/(√2)) +1 +(√(1+((π/(√2))+1)^2 )))−ln(1+(√2)).](Q53603.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19

| ||
Question and Answers Forum | ||
Question Number 53463 by maxmathsup by imad last updated on 22/Jan/19 | ||
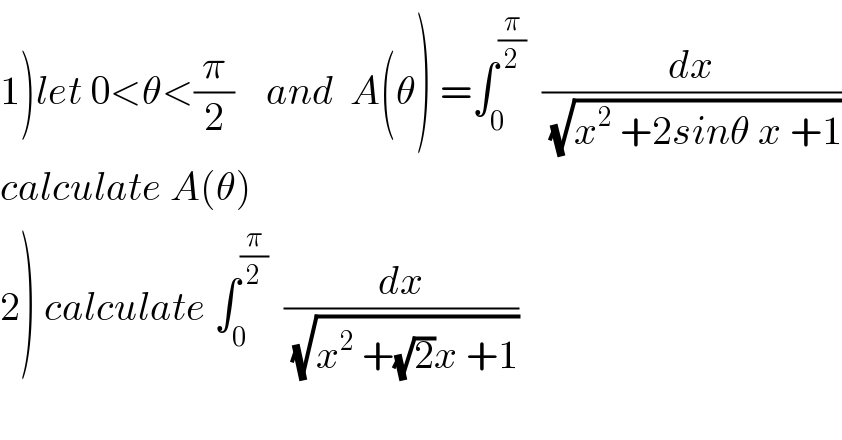 | ||
Commented bymaxmathsup by imad last updated on 23/Jan/19 | ||
![1) we have A(θ) =∫_0 ^(π/2) (dx/(√(x^2 +2x sinθ +sin^2 θ +cos^2 θ))) =∫_0 ^(π/2) (dx/(√((x+sinθ)^(2 ) +cos^2 θ))) changement x+sinθ=t cosθ give t =((x+sinθ)/(cosθ)) A(θ) = ∫_(tanθ) ^((π/(2cosθ))+tanθ) ((cosθ dt)/(cosθ(√(1+t^2 )))) = ∫_(tanθ) ^((π/(2cosθ)) +tanθ) (dt/(√(1+t^2 ))) =[argsh(t)]_(tanθ) ^((π/(2cosθ))+tanθ) =ln(t+(√(1+t^2 ))]_(tanθ) ^((π/(2cosθ)) +tanθ) = ln((π/(2cosθ)) +tanθ +(√(1+((π/(2cosθ))+tanθ)^2 ))) −ln(tanθ +(√(1+tan^2 θ))) 2) ∫_0 ^(π/2) (dx/(√(x^2 +(√2)x +1))) =A((π/4)) =ln((π/(2 cos((π/4)))) +tan((π/4))+(√(1+((π/(2cos((π/4))))+tan((π/4))^2 )) −ln(tan((π/4))+(√(1+tan^2 ((π/4))))) =ln((π/(√2)) +1 +(√(1+((π/(√2))+1)^2 )))−ln(1+(√2)).](Q53603.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19 | ||
 | ||
| ||