
Question and Answers Forum
Question Number 53470 by maxmathsup by imad last updated on 22/Jan/19
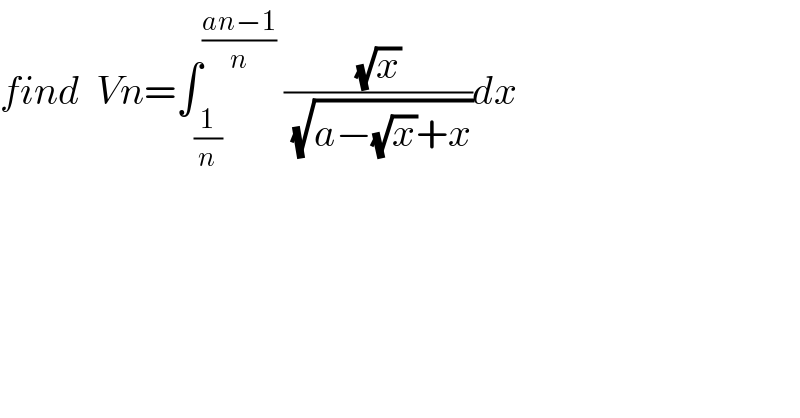
Commented by maxmathsup by imad last updated on 24/Jan/19
![changement (√x)=t give x=t^2 ⇒dx =2tdt and V_n = ∫_(1/(√n)) ^(√((an−1)/n)) (t/(√(a−t+t^2 ))) (2t)dt =2 ∫_(1/(√n)) ^(√((an−1)/n)) (t^2 /(√(t^2 −2(1/2)t +(1/4)+a−(1/4))))dt =2 ∫_(1/(√n)) ^(√((an−1)/n)) (t^2 /(√((t−(1/2))^2 +((4a−1)/4)))) let suppose a>(1/4) ⇒ V_n =_(t−(1/2)=((√(4a−1))/2)u) 2∫_(((2/(√n))−1)/(√(4a−1))) ^((2(√((an−1)/n))−1)/(√(4a−1))) (((((√(4a−1))/2)u+(1/2))^2 )/(((√(4a−1))/2)(√(1+u^2 )))) ((√(4a−1))/2) du = 2 ∫_((2−(√n))/((√n)(√(4a−1)))) ^((2((√(4a−1))−(√n))/((√n)(√(4a−1)))) (1/4) (((4a−1)u^2 +2(√(4a−1))u +1)/(√(1+u^2 ))) du =(1/2) ∫_α_n ^β_n (((4a−1)u^2 +2(√(4a−1))u +1)/(√(1+u^2 ))) du =((4a−1)/2) ∫_α_n ^β_n ((u^2 +1 −1)/(√(1+u^2 ))) + (√(4a−1))∫_α_n ^β_n (u/(√(1+u^2 ))) du +(1/2) ∫_α_n ^β_n (du/(√(1+u^2 ))) ∫_α_n ^β_n (du/(√(1+u^2 ))) =[ln(1+(√(1+x^2 ]_α_n ^β_n ))=ln(1+(√(1+β_n ^2 )))−ln(1+(√(1+α_n ^2 ))) ∫_α_n ^β_n (u/(√(1+u^2 ))) du =[(√(1+u^2 ))]_α_n ^β_n =(√(1+β_n ^2 ))−(√(1+α_n ^2 )) ∫_α_n ^β_n ((u^2 +1−1)/(√(1+u^2 ))) du =∫_α_n ^β_n (√(1+u^2 ))du −∫_α_n ^β_n (du/(√(1+u^2 ))) =.....](Q53674.png)
| ||
Question and Answers Forum | ||
Question Number 53470 by maxmathsup by imad last updated on 22/Jan/19 | ||
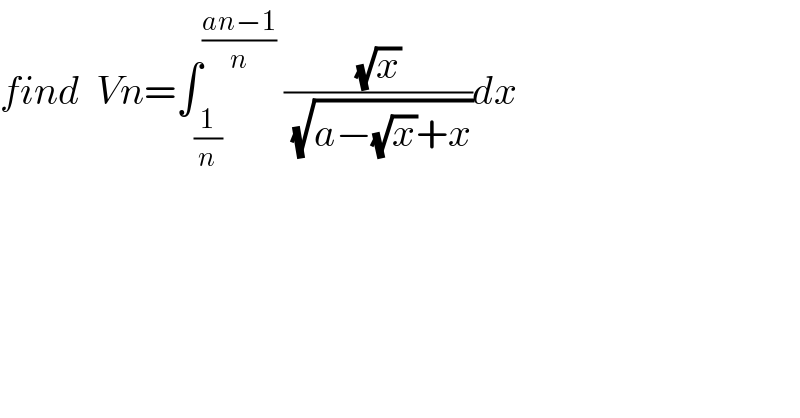 | ||
Commented by maxmathsup by imad last updated on 24/Jan/19 | ||
![changement (√x)=t give x=t^2 ⇒dx =2tdt and V_n = ∫_(1/(√n)) ^(√((an−1)/n)) (t/(√(a−t+t^2 ))) (2t)dt =2 ∫_(1/(√n)) ^(√((an−1)/n)) (t^2 /(√(t^2 −2(1/2)t +(1/4)+a−(1/4))))dt =2 ∫_(1/(√n)) ^(√((an−1)/n)) (t^2 /(√((t−(1/2))^2 +((4a−1)/4)))) let suppose a>(1/4) ⇒ V_n =_(t−(1/2)=((√(4a−1))/2)u) 2∫_(((2/(√n))−1)/(√(4a−1))) ^((2(√((an−1)/n))−1)/(√(4a−1))) (((((√(4a−1))/2)u+(1/2))^2 )/(((√(4a−1))/2)(√(1+u^2 )))) ((√(4a−1))/2) du = 2 ∫_((2−(√n))/((√n)(√(4a−1)))) ^((2((√(4a−1))−(√n))/((√n)(√(4a−1)))) (1/4) (((4a−1)u^2 +2(√(4a−1))u +1)/(√(1+u^2 ))) du =(1/2) ∫_α_n ^β_n (((4a−1)u^2 +2(√(4a−1))u +1)/(√(1+u^2 ))) du =((4a−1)/2) ∫_α_n ^β_n ((u^2 +1 −1)/(√(1+u^2 ))) + (√(4a−1))∫_α_n ^β_n (u/(√(1+u^2 ))) du +(1/2) ∫_α_n ^β_n (du/(√(1+u^2 ))) ∫_α_n ^β_n (du/(√(1+u^2 ))) =[ln(1+(√(1+x^2 ]_α_n ^β_n ))=ln(1+(√(1+β_n ^2 )))−ln(1+(√(1+α_n ^2 ))) ∫_α_n ^β_n (u/(√(1+u^2 ))) du =[(√(1+u^2 ))]_α_n ^β_n =(√(1+β_n ^2 ))−(√(1+α_n ^2 )) ∫_α_n ^β_n ((u^2 +1−1)/(√(1+u^2 ))) du =∫_α_n ^β_n (√(1+u^2 ))du −∫_α_n ^β_n (du/(√(1+u^2 ))) =.....](Q53674.png) | ||