
Question and Answers Forum
Question Number 53593 by ajfour last updated on 23/Jan/19

Commented by ajfour last updated on 23/Jan/19
![Having removed the largest cube from a hemisphere, it can rest in equilibrium on a rough incline plane of inclination α, in the manner shown. Find θ. (source: Statics & Dynamics by S.L. Loney) Answer given: θ=sin^(−1) [((8(3π−(√6)))/(9π−8))sin α].](Q53594.png)
Answered by mr W last updated on 23/Jan/19

Commented by mr W last updated on 23/Jan/19
![R=radius of sphere a^2 +a^2 +(2a)^2 =R^2 ⇒a=(R/(√6)) M=mass of hemisphere m=mass of cube M=((2πR^3 ρ)/3) m=8a^3 ρ=((4R^3 ρ)/(3(√6)))=((2M)/(π(√6))) center of mass of hemisphere: b=((3R)/8) center of mass of hemisphere with hole: c=((Mb−ma)/(M−m))=((((M3R)/8)−((2M)/(π(√6)))×(R/(√6)))/(M−((2M)/(π(√6)))))=((R(9π−8))/(8(3π−(√6)))) (c/(sin α))=(R/(sin (π−θ))) ⇒sin θ=(R/c) sin α=((8(3π−(√6)))/(9π−8))×sin α ⇒θ=sin^(−1) [((8(3π−(√6)))/(9π−8))×sin α]](Q53598.png)
Commented by ajfour last updated on 23/Jan/19

Commented by mr W last updated on 23/Jan/19
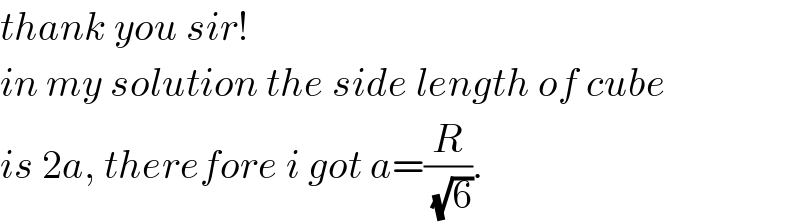
Commented by ajfour last updated on 23/Jan/19

Answered by ajfour last updated on 23/Jan/19

Commented by mr W last updated on 23/Jan/19

