Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 53595 by ajfour last updated on 23/Jan/19

Commented by ajfour last updated on 24/Jan/19

Commented by ajfour last updated on 24/Jan/19

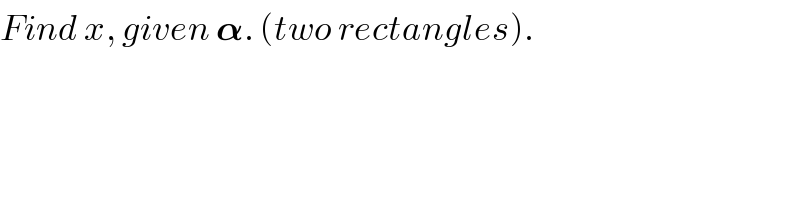
Find x, given 𝛂. (two rectangles).

$${Find}\:{x},\:{given}\:\boldsymbol{\alpha}.\:\left({two}\:{rectangles}\right). \\ $$

Commented by mr W last updated on 24/Jan/19

Commented by ajfour last updated on 24/Jan/19

∠EAF is a right angle too, Sir. it′ll be the same equation; 1−x^4 =kx , if k=tan α i just tried to depict it geometricaly.

$$\angle{EAF}\:{is}\:{a}\:{right}\:{angle}\:{too},\:{Sir}. \\ $$$${it}'{ll}\:{be}\:{the}\:{same}\:{equation};\: \\ $$$$\mathrm{1}−{x}^{\mathrm{4}} ={kx}\:\:,\:{if}\:{k}=\mathrm{tan}\:\alpha \\ $$$${i}\:{just}\:{tried}\:{to}\:{depict}\:{it}\:{geometricaly}. \\ $$

Commented by mr W last updated on 24/Jan/19

great idea!

$${great}\:{idea}! \\ $$

Answered by ajfour last updated on 23/Jan/19

Commented by mr W last updated on 24/Jan/19

A(R,h) y=cx^2 with c=1 y′=2cx x_P =R+R cos θ=R(1+cos θ) y_P =h−R sin θ=cx_P ^2 =cR^2 (1+cos θ)^2 ⇒h=R[sin θ+cR(1+cos θ)^2 ] y_P ′=2cR(1+cos θ)=(1/(tan θ)) ⇒tan θ+sin θ=(1/(2cR)) ...(i) B(r,k) ⇒k=r[sin φ+cr(1+cos φ)^2 ] ⇒tan φ+sin φ=(1/(2cr)) ...(ii) h−k=(√((R+r)^2 −(R−r)^2 ))=2(√(Rr)) ⇒R[sin θ+cR(1+cos θ)^2 ]−r[sin φ+cr(1+cos φ)^2 ]=2(√(Rr)) ...(iii) ...... 3 eqn. with 3 unknowns r,φ,θ from (i): tan θ+sin θ=(1/(2cR))=(4/k)⇒k=8cR with t=tan (θ/2) ((2t)/(1−t^2 ))+((2t)/(1+t^2 ))=(4/k) t^4 +kt−1=0 ⇒t=f(k)=.... from (ii): ⇒cr=(1/(2(tan φ+sin φ))) from (iii): ⇒((k[k+4t(1+t^2 )])/(8(1+t^2 )^2 ))−(1/(tan φ+sin φ))[sin φ+(((1+cos φ)^2 )/(2(tan φ+sin φ)))]=(√(k/(tan φ+sin φ))) ⇒φ=.....

$${A}\left({R},{h}\right) \\ $$$${y}={cx}^{\mathrm{2}} \:{with}\:{c}=\mathrm{1} \\ $$$${y}'=\mathrm{2}{cx} \\ $$$${x}_{{P}} ={R}+{R}\:\mathrm{cos}\:\theta={R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$${y}_{{P}} ={h}−{R}\:\mathrm{sin}\:\theta={cx}_{{P}} ^{\mathrm{2}} ={cR}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow{h}={R}\left[\mathrm{sin}\:\theta+{cR}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right] \\ $$$${y}_{{P}} '=\mathrm{2}{cR}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\mathrm{tan}\:\theta+\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{cR}}\:\:\:\:\:...\left({i}\right) \\ $$$${B}\left({r},{k}\right) \\ $$$$\Rightarrow{k}={r}\left[\mathrm{sin}\:\phi+{cr}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)^{\mathrm{2}} \right] \\ $$$$\Rightarrow\mathrm{tan}\:\phi+\mathrm{sin}\:\phi=\frac{\mathrm{1}}{\mathrm{2}{cr}}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${h}−{k}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{Rr}} \\ $$$$\Rightarrow{R}\left[\mathrm{sin}\:\theta+{cR}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right]−{r}\left[\mathrm{sin}\:\phi+{cr}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)^{\mathrm{2}} \right]=\mathrm{2}\sqrt{{Rr}}\:\:\:...\left({iii}\right) \\ $$$$......\:\mathrm{3}\:{eqn}.\:{with}\:\mathrm{3}\:{unknowns}\:{r},\phi,\theta \\ $$$${from}\:\left({i}\right): \\ $$$$\mathrm{tan}\:\theta+\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{cR}}=\frac{\mathrm{4}}{{k}}\Rightarrow{k}=\mathrm{8}{cR} \\ $$$${with}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\mathrm{4}}{{k}} \\ $$$${t}^{\mathrm{4}} +{kt}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}={f}\left({k}\right)=.... \\ $$$${from}\:\left({ii}\right): \\ $$$$\Rightarrow{cr}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{tan}\:\phi+\mathrm{sin}\:\phi\right)} \\ $$$${from}\:\left({iii}\right): \\ $$$$\Rightarrow\frac{{k}\left[{k}+\mathrm{4}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]}{\mathrm{8}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{tan}\:\phi+\mathrm{sin}\:\phi}\left[\mathrm{sin}\:\phi+\frac{\left(\mathrm{1}+\mathrm{cos}\:\phi\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{tan}\:\phi+\mathrm{sin}\:\phi\right)}\right]=\sqrt{\frac{{k}}{\mathrm{tan}\:\phi+\mathrm{sin}\:\phi}} \\ $$$$\Rightarrow\phi=..... \\ $$

Commented by ajfour last updated on 01/Feb/19

Thats what sir, we cant even get centre of circles, given the radii, biquadratic problem..

$${Thats}\:{what}\:{sir},\:{we}\:{cant}\:{even}\:{get} \\ $$$${centre}\:{of}\:{circles},\:{given}\:{the}\:{radii}, \\ $$$${biquadratic}\:{problem}..\:\:\:\:\:\:\: \\ $$

Commented by mr W last updated on 24/Jan/19

t^4 +kt−1=0 should be solvable. can MJS sir help?

$${t}^{\mathrm{4}} +{kt}−\mathrm{1}=\mathrm{0} \\ $$$${should}\:{be}\:{solvable}.\:{can}\:{MJS}\:{sir}\:{help}? \\ $$

Commented by MJS last updated on 24/Jan/19

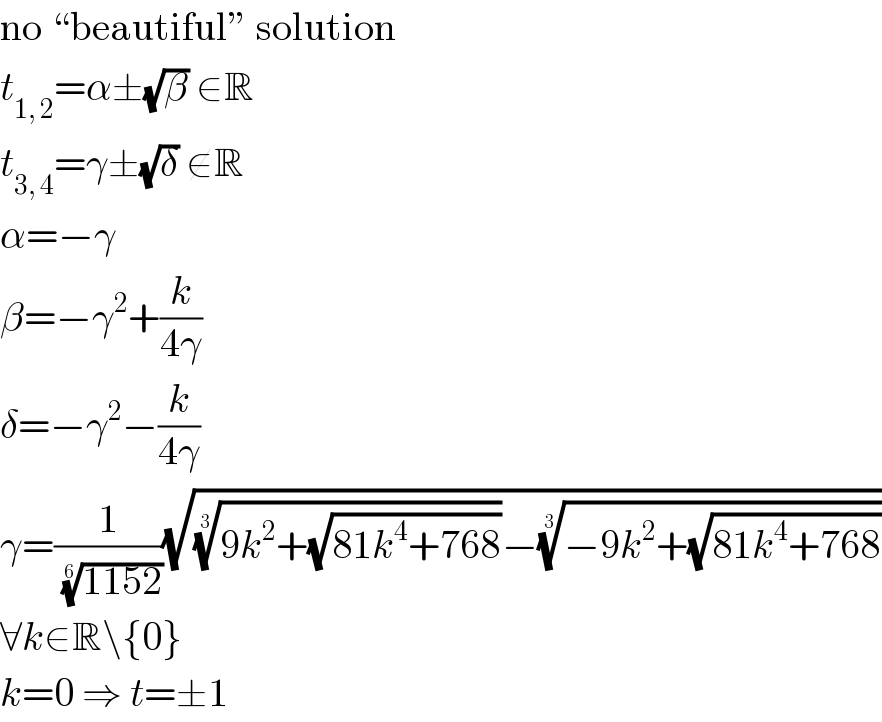
no “beautiful” solution t_(1, 2) =α±(√β) ∈R t_(3, 4) =γ±(√δ) ∉R α=−γ β=−γ^2 +(k/(4γ)) δ=−γ^2 −(k/(4γ)) γ=(1/((1152))^(1/6) )(√(((9k^2 +(√(81k^4 +768))))^(1/3) −((−9k^2 +(√(81k^4 +768))))^(1/3) )) ∀k∈R\{0} k=0 ⇒ t=±1

$$\mathrm{no}\:``\mathrm{beautiful}''\:\mathrm{solution} \\ $$$${t}_{\mathrm{1},\:\mathrm{2}} =\alpha\pm\sqrt{\beta}\:\in\mathbb{R} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} =\gamma\pm\sqrt{\delta}\:\notin\mathbb{R} \\ $$$$\alpha=−\gamma \\ $$$$\beta=−\gamma^{\mathrm{2}} +\frac{{k}}{\mathrm{4}\gamma} \\ $$$$\delta=−\gamma^{\mathrm{2}} −\frac{{k}}{\mathrm{4}\gamma} \\ $$$$\gamma=\frac{\mathrm{1}}{\sqrt[{\mathrm{6}}]{\mathrm{1152}}}\sqrt{\sqrt[{\mathrm{3}}]{\mathrm{9}{k}^{\mathrm{2}} +\sqrt{\mathrm{81}{k}^{\mathrm{4}} +\mathrm{768}}}−\sqrt[{\mathrm{3}}]{−\mathrm{9}{k}^{\mathrm{2}} +\sqrt{\mathrm{81}{k}^{\mathrm{4}} +\mathrm{768}}}} \\ $$$$\forall{k}\in\mathbb{R}\backslash\left\{\mathrm{0}\right\} \\ $$$${k}=\mathrm{0}\:\Rightarrow\:{t}=\pm\mathrm{1} \\ $$

Commented by mr W last updated on 24/Jan/19

sir, it′s a beautiful solution!

$${sir},\:{it}'{s}\:{a}\:\mathrm{beautiful}\:\mathrm{solution}! \\ $$

Commented by ajfour last updated on 24/Jan/19

thanks afterall Sir!

$${thanks}\:{afterall}\:{Sir}! \\ $$

Commented by MJS last updated on 24/Jan/19

you′re welcome

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$

Commented by MJS last updated on 24/Jan/19

trying something else: parabola: y=ax^2 normal in P= ((p),((ap^2 )) ): y=−(1/(2ap))x+((2a^2 p^2 +1)/(2a)) horizontal: y=h normal∩horizontal = C= ((x_C ),(y_C ) ) C= (((p(2p^2 +1−2h))),(h) ) ∣CP∣=x_C ⇒ we can calculate the 3^(rd) parameter when 2 are given a=((h+(√(4h^2 −3p^2 )))/(3p^2 )) h=p(−ap+(√(4a^2 p^2 +1))) p=((√(2ah−1+(√(16a^2 h^2 −4ah+1))))/((√6)a)) on the other hand two circles both touching the y−axis and each others can be calculated c_1 : (x−r_1 )^2 +(y−h_1 )^2 =r_1 ^2 c_2 : (x−r_2 )^2 +(y−h_2 )^2 =r_2 ^2 c_1 ∩c_2 =exactly 1 solution ⇒ ⇒ 4r_1 r_2 =(h_1 −h_2 )^2 ...not yet sure where this will lead to...

$$\mathrm{trying}\:\mathrm{something}\:\mathrm{else}: \\ $$$$\mathrm{parabola}:\:{y}={ax}^{\mathrm{2}} \\ $$$$\mathrm{normal}\:\mathrm{in}\:{P}=\begin{pmatrix}{{p}}\\{{ap}^{\mathrm{2}} }\end{pmatrix}:\:{y}=−\frac{\mathrm{1}}{\mathrm{2}{ap}}{x}+\frac{\mathrm{2}{a}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$$$\mathrm{horizontal}:\:{y}={h} \\ $$$$\mathrm{normal}\cap\mathrm{horizontal}\:=\:{C}=\begin{pmatrix}{{x}_{{C}} }\\{{y}_{{C}} }\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{{p}\left(\mathrm{2}{p}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{h}\right)}\\{{h}}\end{pmatrix} \\ $$$$\mid{CP}\mid={x}_{{C}} \:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{parameter} \\ $$$$\mathrm{when}\:\mathrm{2}\:\mathrm{are}\:\mathrm{given} \\ $$$${a}=\frac{{h}+\sqrt{\mathrm{4}{h}^{\mathrm{2}} −\mathrm{3}{p}^{\mathrm{2}} }}{\mathrm{3}{p}^{\mathrm{2}} } \\ $$$${h}={p}\left(−{ap}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${p}=\frac{\sqrt{\mathrm{2}{ah}−\mathrm{1}+\sqrt{\mathrm{16}{a}^{\mathrm{2}} {h}^{\mathrm{2}} −\mathrm{4}{ah}+\mathrm{1}}}}{\sqrt{\mathrm{6}}{a}} \\ $$$$ \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand}\:\mathrm{two}\:\mathrm{circles}\:\mathrm{both}\:\mathrm{touching} \\ $$$$\mathrm{the}\:{y}−\mathrm{axis}\:\mathrm{and}\:\mathrm{each}\:\mathrm{others}\:\mathrm{can}\:\mathrm{be}\:\mathrm{calculated} \\ $$$${c}_{\mathrm{1}} :\:\left({x}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({y}−{h}_{\mathrm{1}} \right)^{\mathrm{2}} ={r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${c}_{\mathrm{2}} :\:\left({x}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}−{h}_{\mathrm{2}} \right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} \cap{c}_{\mathrm{2}} =\mathrm{exactly}\:\mathrm{1}\:\mathrm{solution}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{2}} =\left({h}_{\mathrm{1}} −{h}_{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$...\mathrm{not}\:\mathrm{yet}\:\mathrm{sure}\:\mathrm{where}\:\mathrm{this}\:\mathrm{will}\:\mathrm{lead}\:\mathrm{to}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com