
Question and Answers Forum
Question Number 53600 by maxmathsup by imad last updated on 23/Jan/19
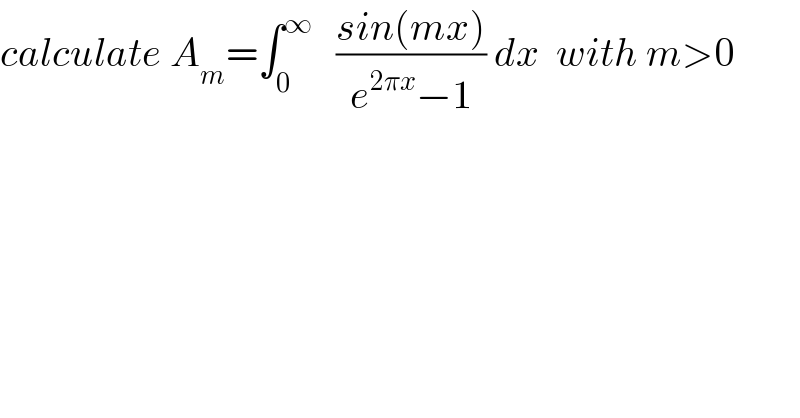
Commented bymaxmathsup by imad last updated on 24/Jan/19
![we have A_m =∫_0 ^∞ ((e^(−2πx) sin(mx))/(1−e^(−2πx) )) dx =Im(∫_0 ^∞ ((e^(−2πx) e^(imx) )/(1−e^(−2πx) ))dx) but ∫_0 ^∞ (e^(−(2π−im)x) /(1−e^(−2πx) ))dx =∫_0 ^∞ e^(−(2π−im)x) (Σ_(p=0) ^∞ e^(−2πp x) ) =Σ_(p=0) ^∞ ∫_0 ^∞ e^(−(2π−im+2pπ)x) dx =Σ_(p=0) ^∞ [−(1/(2π−im+2pπ)) e^(−(2π−im+2pπ)x) ]^(+∞) _0 =Σ_(p=0) ^∞ (1/((2+2p)π −im)) =Σ_(p=0) ^∞ (((2+2p)π+im)/((2+2p)^2 π^2 +m^2 )) ⇒ A_m =Σ_(p=0) ^∞ (m/(4(p+1)^2 π^2 +m^2 )) and A_m can be calculated by fourier series ....be continued...](Q53669.png)
| ||
Question and Answers Forum | ||
Question Number 53600 by maxmathsup by imad last updated on 23/Jan/19 | ||
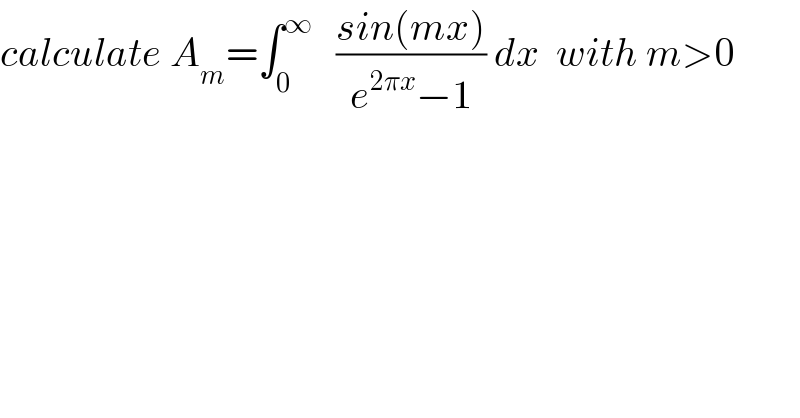 | ||
Commented bymaxmathsup by imad last updated on 24/Jan/19 | ||
![we have A_m =∫_0 ^∞ ((e^(−2πx) sin(mx))/(1−e^(−2πx) )) dx =Im(∫_0 ^∞ ((e^(−2πx) e^(imx) )/(1−e^(−2πx) ))dx) but ∫_0 ^∞ (e^(−(2π−im)x) /(1−e^(−2πx) ))dx =∫_0 ^∞ e^(−(2π−im)x) (Σ_(p=0) ^∞ e^(−2πp x) ) =Σ_(p=0) ^∞ ∫_0 ^∞ e^(−(2π−im+2pπ)x) dx =Σ_(p=0) ^∞ [−(1/(2π−im+2pπ)) e^(−(2π−im+2pπ)x) ]^(+∞) _0 =Σ_(p=0) ^∞ (1/((2+2p)π −im)) =Σ_(p=0) ^∞ (((2+2p)π+im)/((2+2p)^2 π^2 +m^2 )) ⇒ A_m =Σ_(p=0) ^∞ (m/(4(p+1)^2 π^2 +m^2 )) and A_m can be calculated by fourier series ....be continued...](Q53669.png) | ||