Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 53623 by turbo msup by abdo last updated on 24/Jan/19

1) study the function f(x)=ln(x+1−(√x)) 2) determine f^(−1) (x) 3) cslculate ∫ f(x)dx snd ∫ f^(−1) (x)dx 4) dtermine ∫ f^(−1) (x^2 +f(x))dx

$$\left.\mathrm{1}\right)\:{study}\:{the}\:{function} \\ $$$${f}\left({x}\right)={ln}\left({x}+\mathrm{1}−\sqrt{{x}}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:{cslculate}\:\:\int\:{f}\left({x}\right){dx}\:{snd} \\ $$$$\int\:{f}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$$\left.\mathrm{4}\right)\:{dtermine}\:\int\:{f}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \:+{f}\left({x}\right)\right){dx} \\ $$$$ \\ $$

Commented by Abdo msup. last updated on 25/Jan/19

1) x∈D_f ⇔x+1−(√x)>0 ⇔t^2 +1−t>0(t=(√x)) t^2 −t +1>0 →Δ=1−4=−3<0 a=1>0 ⇒ t^2 −t +1 >0 ∀t ⇒ D_f =[0,+∞[ we have f(x)=ln(x)+ln(1+(1/x)−(1/(√x))) ⇒ lim_(x→+∞) f(x)=lim_(x→+∞) ln(x)=+∞ lim_(x→+∞) ((f(x))/x) =lim_(x→+∞) ((ln(x))/x) =0 so the graph have a parabol branch in (oy) direction derivative f^′ (x)= (((x+1−(√x))^, )/(x+1−(√x))) =((1−(1/(2(√x))))/(x+1−(√x))) =((2(√x)−1)/(2(√x)(x+1−(√x)))) f^′ (x)=0 ⇔2(√x)−1=0 ⇔(√x)=(1/2) ⇔x=(1/4) f^′ (x)≥0 ⇔x≥(1/4) variations of f(x) −−−−−−−−−−−−−−−−− x 0 (1/4) +∞ f^, (x) − 0 + f(x) 0 decr. f((1/4)) incr. −−−−−−−−−−−−−−−−−−− f((1/4))=ln((5/4) −(1/2)) =ln((3/4))=ln(3)−2ln(2) intersection between graph and (ox) f(x)=0 ⇔ln(x+1−(√x))=0 ⇔x+1−(√x)=1 x=(√x) ⇔x^2 =x ⇔ x=0 or x=1 the points are 0(0,0) and A(1,0) rest drawing graph..be cintinued...

$$\left.\mathrm{1}\right)\:{x}\in{D}_{{f}} \:\Leftrightarrow{x}+\mathrm{1}−\sqrt{{x}}>\mathrm{0}\:\Leftrightarrow{t}^{\mathrm{2}} \:+\mathrm{1}−{t}>\mathrm{0}\left({t}=\sqrt{{x}}\right) \\ $$$${t}^{\mathrm{2}} \:−{t}\:+\mathrm{1}>\mathrm{0}\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}<\mathrm{0}\:\:\:{a}=\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} −{t}\:+\mathrm{1}\:>\mathrm{0}\:\forall{t}\:\Rightarrow\:{D}_{{f}} =\left[\mathrm{0},+\infty\left[\right.\right. \\ $$$${we}\:{have}\:{f}\left({x}\right)={ln}\left({x}\right)+{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\sqrt{{x}}}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={lim}_{{x}\rightarrow+\infty} {ln}\left({x}\right)=+\infty \\ $$$${lim}_{{x}\rightarrow+\infty} \:\frac{{f}\left({x}\right)}{{x}}\:={lim}_{{x}\rightarrow+\infty} \:\:\frac{{ln}\left({x}\right)}{{x}}\:=\mathrm{0}\:{so}\:{the}\:{graph} \\ $$$${have}\:{a}\:{parabol}\:{branch}\:{in}\:\left({oy}\right)\:{direction} \\ $$$${derivative}\:{f}^{'} \left({x}\right)=\:\frac{\left({x}+\mathrm{1}−\sqrt{{x}}\right)^{,} }{{x}+\mathrm{1}−\sqrt{{x}}} \\ $$$$=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{{x}+\mathrm{1}−\sqrt{{x}}}\:=\frac{\mathrm{2}\sqrt{{x}}−\mathrm{1}}{\mathrm{2}\sqrt{{x}}\left({x}+\mathrm{1}−\sqrt{{x}}\right)} \\ $$$${f}^{'} \left({x}\right)=\mathrm{0}\:\Leftrightarrow\mathrm{2}\sqrt{{x}}−\mathrm{1}=\mathrm{0}\:\Leftrightarrow\sqrt{{x}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Leftrightarrow{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}^{'} \left({x}\right)\geqslant\mathrm{0}\:\Leftrightarrow{x}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${variations}\:{of}\:{f}\left({x}\right) \\ $$$$−−−−−−−−−−−−−−−−− \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{,} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:+ \\ $$$${f}\left({x}\right)\:\:\:\:\mathrm{0}\:\:\:{decr}.\:\:\:\:\:{f}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\:\:\:{incr}. \\ $$$$−−−−−−−−−−−−−−−−−−− \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)={ln}\left(\frac{\mathrm{5}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)\:={ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)={ln}\left(\mathrm{3}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$${intersection}\:{between}\:{graph}\:{and}\:\left({ox}\right) \\ $$$${f}\left({x}\right)=\mathrm{0}\:\Leftrightarrow{ln}\left({x}+\mathrm{1}−\sqrt{{x}}\right)=\mathrm{0}\:\Leftrightarrow{x}+\mathrm{1}−\sqrt{{x}}=\mathrm{1} \\ $$$${x}=\sqrt{{x}}\:\Leftrightarrow{x}^{\mathrm{2}} \:={x}\:\Leftrightarrow\:{x}=\mathrm{0}\:{or}\:{x}=\mathrm{1} \\ $$$${the}\:{points}\:{are}\:\mathrm{0}\left(\mathrm{0},\mathrm{0}\right)\:{and}\:{A}\left(\mathrm{1},\mathrm{0}\right) \\ $$$${rest}\:{drawing}\:{graph}..{be}\:{cintinued}... \\ $$

Commented by Abdo msup. last updated on 25/Jan/19

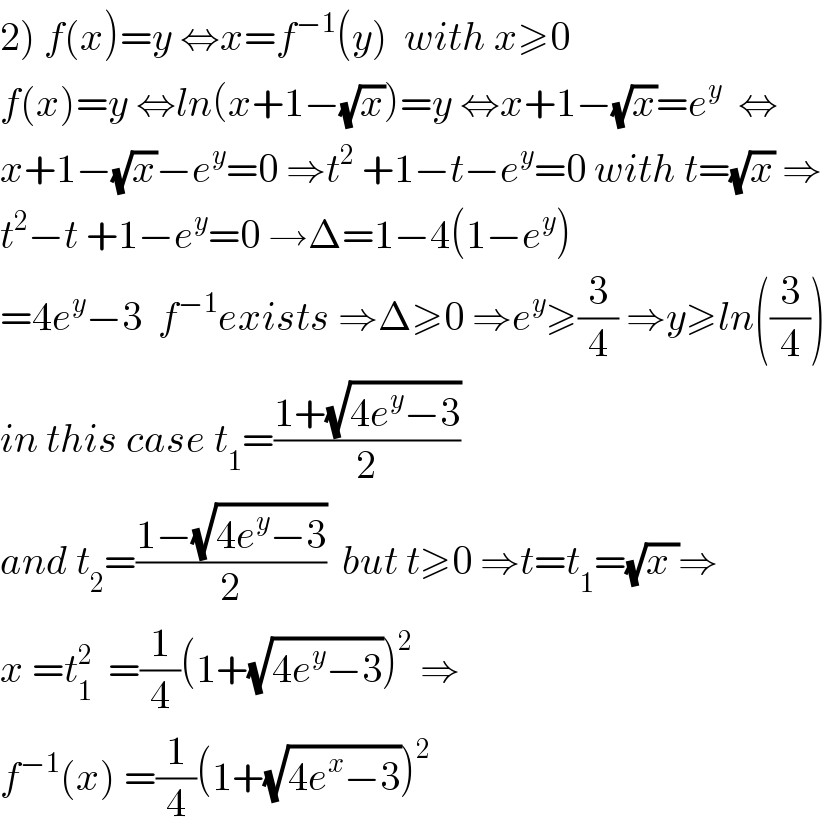
2) f(x)=y ⇔x=f^(−1) (y) with x≥0 f(x)=y ⇔ln(x+1−(√x))=y ⇔x+1−(√x)=e^y ⇔ x+1−(√x)−e^y =0 ⇒t^2 +1−t−e^y =0 with t=(√x) ⇒ t^2 −t +1−e^y =0 →Δ=1−4(1−e^y ) =4e^y −3 f^(−1) exists ⇒Δ≥0 ⇒e^y ≥(3/4) ⇒y≥ln((3/4)) in this case t_1 =((1+(√(4e^y −3)))/2) and t_2 =((1−(√(4e^y −3)))/2) but t≥0 ⇒t=t_1 =(√(x ))⇒ x =t_1 ^2 =(1/4)(1+(√(4e^y −3)))^2 ⇒ f^(−1) (x) =(1/4)(1+(√(4e^x −3)))^2

$$\left.\mathrm{2}\right)\:{f}\left({x}\right)={y}\:\Leftrightarrow{x}={f}^{−\mathrm{1}} \left({y}\right)\:\:{with}\:{x}\geqslant\mathrm{0} \\ $$$${f}\left({x}\right)={y}\:\Leftrightarrow{ln}\left({x}+\mathrm{1}−\sqrt{{x}}\right)={y}\:\Leftrightarrow{x}+\mathrm{1}−\sqrt{{x}}={e}^{{y}} \:\:\Leftrightarrow \\ $$$${x}+\mathrm{1}−\sqrt{{x}}−{e}^{{y}} =\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} \:+\mathrm{1}−{t}−{e}^{{y}} =\mathrm{0}\:{with}\:{t}=\sqrt{{x}}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} −{t}\:+\mathrm{1}−{e}^{{y}} =\mathrm{0}\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}\left(\mathrm{1}−{e}^{{y}} \right) \\ $$$$=\mathrm{4}{e}^{{y}} −\mathrm{3}\:\:{f}^{−\mathrm{1}} {exists}\:\Rightarrow\Delta\geqslant\mathrm{0}\:\Rightarrow{e}^{{y}} \geqslant\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow{y}\geqslant{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${in}\:{this}\:{case}\:{t}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{4}{e}^{{y}} −\mathrm{3}}}{\mathrm{2}} \\ $$$${and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{4}{e}^{{y}} −\mathrm{3}}}{\mathrm{2}}\:\:{but}\:{t}\geqslant\mathrm{0}\:\Rightarrow{t}={t}_{\mathrm{1}} =\sqrt{{x}\:}\Rightarrow \\ $$$${x}\:={t}_{\mathrm{1}} ^{\mathrm{2}} \:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\sqrt{\mathrm{4}{e}^{{y}} −\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\sqrt{\mathrm{4}{e}^{{x}} −\mathrm{3}}\right)^{\mathrm{2}} \\ $$

Commented by Abdo msup. last updated on 25/Jan/19

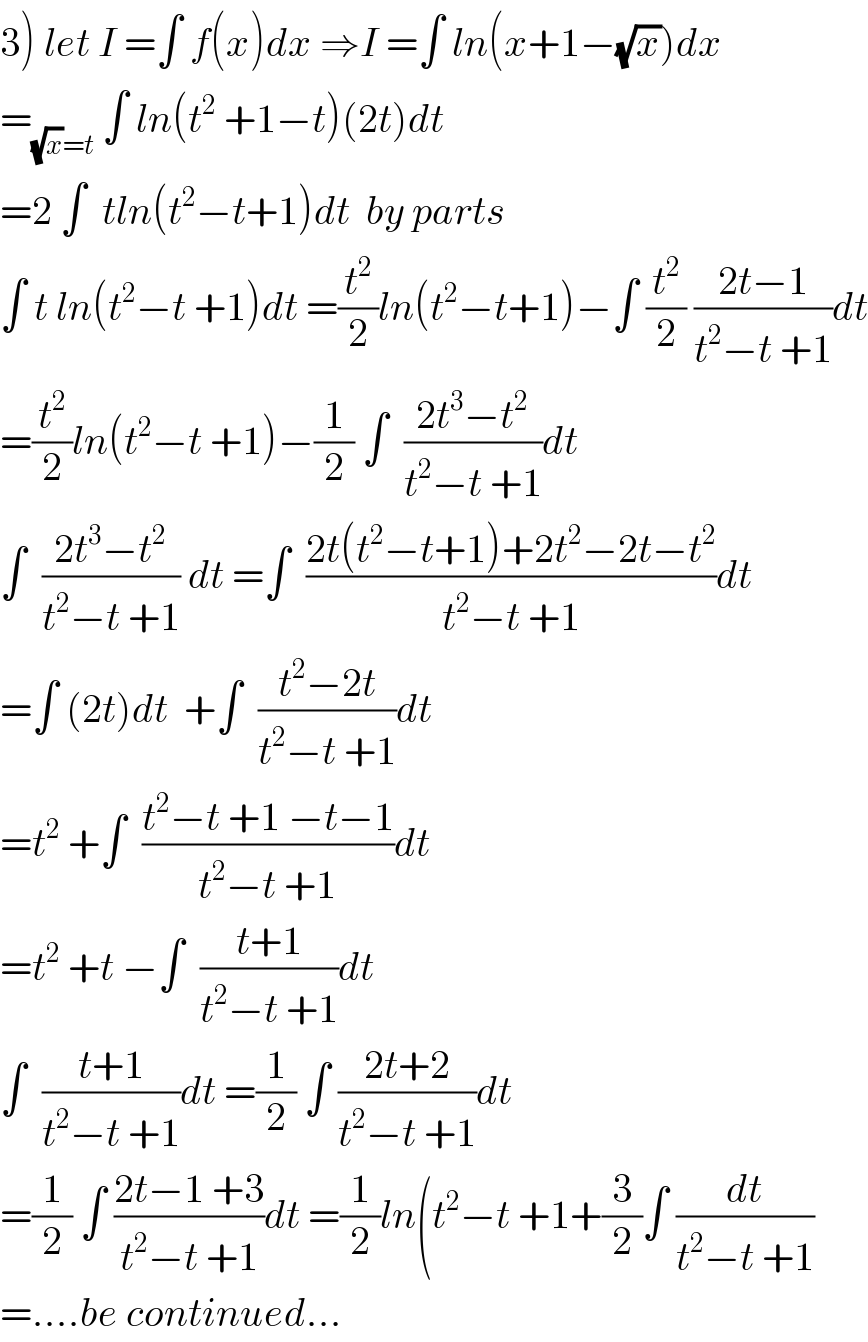
3) let I =∫ f(x)dx ⇒I =∫ ln(x+1−(√x))dx =_((√x)=t) ∫ ln(t^2 +1−t)(2t)dt =2 ∫ tln(t^2 −t+1)dt by parts ∫ t ln(t^2 −t +1)dt =(t^2 /2)ln(t^2 −t+1)−∫ (t^2 /2) ((2t−1)/(t^2 −t +1))dt =(t^2 /2)ln(t^2 −t +1)−(1/2) ∫ ((2t^3 −t^2 )/(t^2 −t +1))dt ∫ ((2t^3 −t^2 )/(t^2 −t +1)) dt =∫ ((2t(t^2 −t+1)+2t^2 −2t−t^2 )/(t^2 −t +1))dt =∫ (2t)dt +∫ ((t^2 −2t)/(t^2 −t +1))dt =t^2 +∫ ((t^2 −t +1 −t−1)/(t^2 −t +1))dt =t^2 +t −∫ ((t+1)/(t^2 −t +1))dt ∫ ((t+1)/(t^2 −t +1))dt =(1/2) ∫ ((2t+2)/(t^2 −t +1))dt =(1/2) ∫ ((2t−1 +3)/(t^2 −t +1))dt =(1/2)ln(t^2 −t +1+(3/2)∫ (dt/(t^2 −t +1)) =....be continued...

$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int\:{f}\left({x}\right){dx}\:\Rightarrow{I}\:=\int\:{ln}\left({x}+\mathrm{1}−\sqrt{{x}}\right){dx} \\ $$$$=_{\sqrt{{x}}={t}} \:\int\:{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}−{t}\right)\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:{tln}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right){dt}\:\:{by}\:{parts} \\ $$$$\int\:{t}\:{ln}\left({t}^{\mathrm{2}} −{t}\:+\mathrm{1}\right){dt}\:=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)−\int\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −{t}\:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:{dt}\:=\int\:\:\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)+\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$=\int\:\left(\mathrm{2}{t}\right){dt}\:\:+\int\:\:\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$={t}^{\mathrm{2}} \:+\int\:\:\frac{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}\:−{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$={t}^{\mathrm{2}} \:+{t}\:−\int\:\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$\int\:\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}{t}+\mathrm{2}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}{t}−\mathrm{1}\:+\mathrm{3}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −{t}\:+\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{{dt}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\right. \\ $$$$=....{be}\:{continued}... \\ $$

Answered by kaivan.ahmadi last updated on 24/Jan/19

first we find D_f x+1−(√x) >0⇒x+1>(√x)⇒x^2 +2x+1>x⇒ x^2 +x+1>0 since x^2 +x+1=0 has no real root and the coefficient of x^2 is positive, then x∈R on the other hand D_(√x) ={x∈R∣x≥0}. so D_f ={x∈R∣x≥0} now we check 1−1 (1,0) , (0,0) ∈f so f is not 1−1 consequently f^(−1) is not exist

$$\mathrm{first}\:\mathrm{we}\:\mathrm{find}\:\mathrm{D}_{\mathrm{f}} \\ $$$$\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{x}}\:>\mathrm{0}\Rightarrow\mathrm{x}+\mathrm{1}>\sqrt{\mathrm{x}}\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}>\mathrm{x}\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{root}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{positive},\:\mathrm{then}\:\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand}\:\mathrm{D}_{\sqrt{\mathrm{x}}} =\left\{\mathrm{x}\in\mathbb{R}\mid\mathrm{x}\geqslant\mathrm{0}\right\}. \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{D}_{\mathrm{f}} =\left\{\mathrm{x}\in\mathbb{R}\mid\mathrm{x}\geqslant\mathrm{0}\right\} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{check}\:\mathrm{1}−\mathrm{1} \\ $$$$\left(\mathrm{1},\mathrm{0}\right)\:,\:\left(\mathrm{0},\mathrm{0}\right)\:\in\mathrm{f}\:\mathrm{so}\:\mathrm{f}\:\mathrm{is}\:\mathrm{not}\:\mathrm{1}−\mathrm{1}\: \\ $$$$\mathrm{consequently}\:\mathrm{f}^{−\mathrm{1}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{exist} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com