
Question and Answers Forum
Question Number 53689 by ajfour last updated on 25/Jan/19

Commented by ajfour last updated on 25/Jan/19
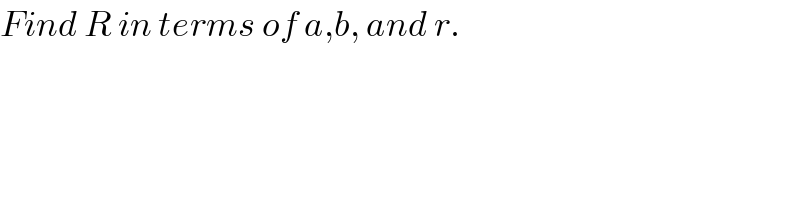
Answered by mr W last updated on 25/Jan/19
![A(0, 2r−b) C(0, −k) k=R+b−2r⇒R=k+2r−b eqn. of big circle: x^2 +(y+k)^2 =R^2 (x^2 /a^2 )+(y^2 /b^2 )=1 ((R^2 −(y+k)^2 )/a^2 )+(y^2 /b^2 )=1 b^2 R^2 −b^2 y^2 −b^2 k^2 −2kb^2 y+a^2 y^2 =a^2 b^2 (a^2 −b^2 )y^2 −2kb^2 y+b^2 (R^2 −a^2 −k^2 )=0 Δ=4k^2 b^4 −4(a^2 −b^2 )b^2 (R^2 −a^2 −k^2 )=0 k^2 b^2 −(a^2 −b^2 )(R^2 −a^2 −k^2 )=0 k^2 b^2 −(a^2 −b^2 )[(k+2r−b)^2 −a^2 −k^2 ]=0 ⇒b^2 k^2 −2(a^2 −b^2 )(2r−b)k−(a^2 −b^2 )(2r−b−a)(2r−b+a)=0 ⇒k=(((a^2 −b^2 )(2r−b)±(√((a^2 −b^2 )[(a^2 −b^2 )(2r−b)^2 +b^2 (2r−b−a)(2r−b+a)])))/b^2 ) ⇒k=(((a^2 −b^2 )(2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 ) ⇒R=2r−b+(((a^2 −b^2 )(2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 ) ⇒R=((a^2 (2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 )](Q53698.png)
Commented by ajfour last updated on 25/Jan/19

Commented by mr W last updated on 25/Jan/19
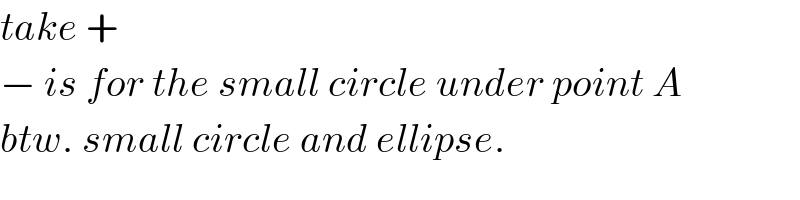
Commented by ajfour last updated on 25/Jan/19
Answered by ajfour last updated on 25/Jan/19
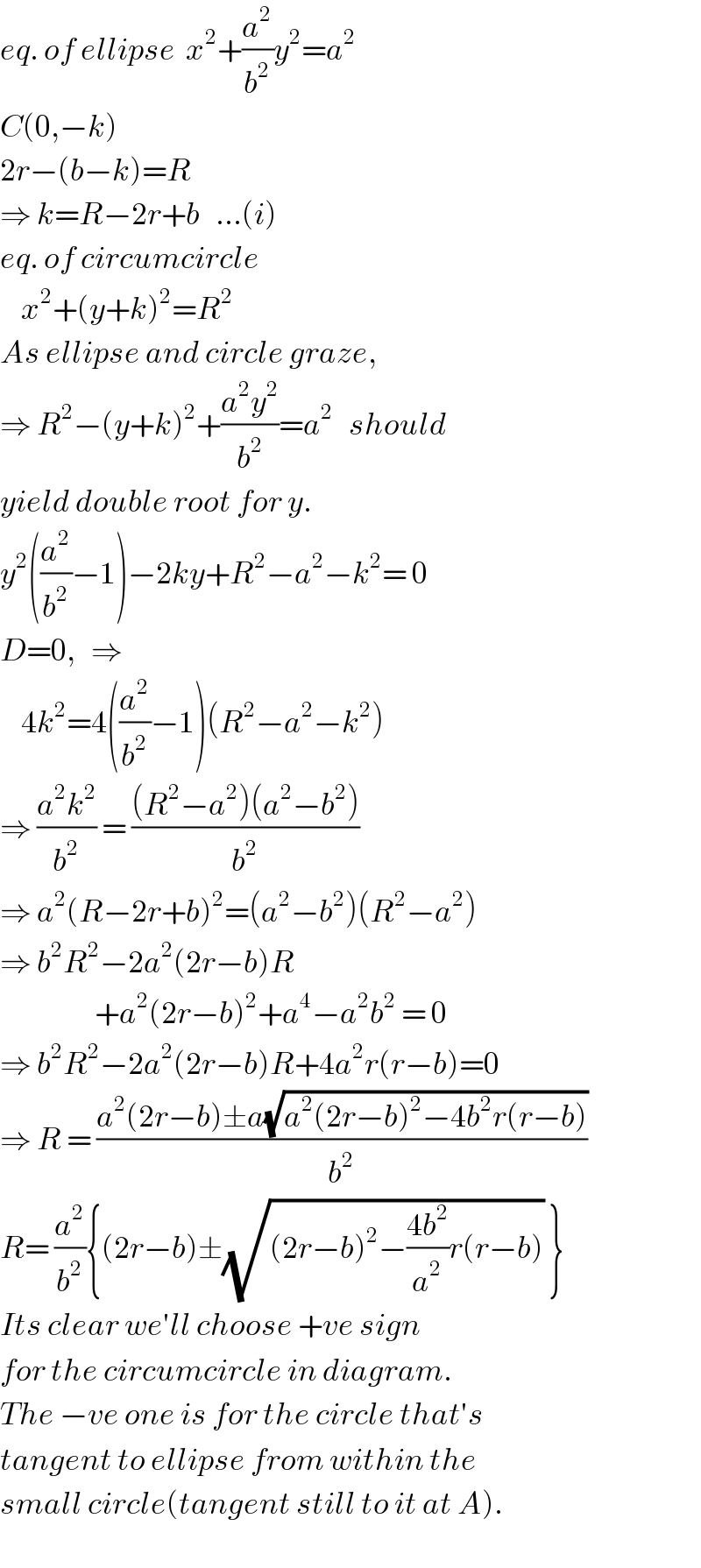
Commented by mr W last updated on 25/Jan/19

