
Question and Answers Forum
Question Number 53694 by gunawan last updated on 25/Jan/19
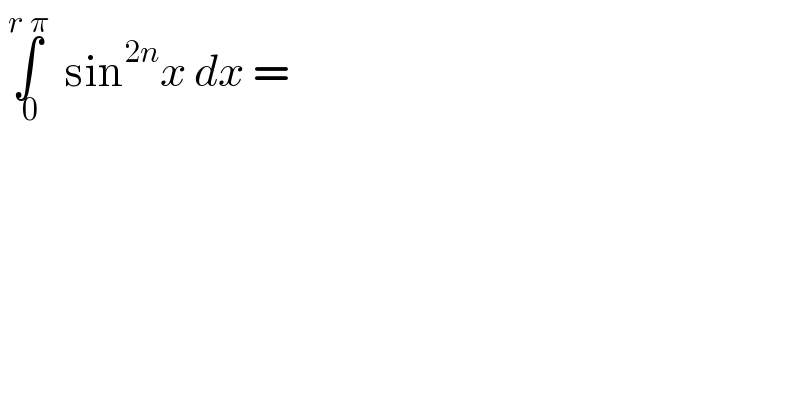
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
![∫_0 ^π sinxdx=∣−cosx∣_0 ^π =−(cosπ−cos0)=2 so the area of each loop of f(x)=sinx is 2 f(x)=sin^(2n) x f(rπ−x)=[sin(rπ−x)]^(2n) =[eitther +sinx or −sinx] but [sin(rπ−x)]^(2n) =sin^(2n) x now ∫_0 ^(2a) f(x)dx=2∫_0 ^a f(x)dx when f(2a−x)=f(x) sinx =sin(2π+x) peridocity 2π ∫_0 ^(rπ) sin^(2n) xdx =∫_0 ^((r/2)×2π) sin^(2n) xdx =(r/2)∫_0 ^(2π) sin^(2n) xdx =(r/2)×2∫_0 ^π sin^(2n) xdx[∫_0 ^(2a) f(x)dx=2∫_0 ^a f(x)dx whenf(2a−x)=f(x)] =2r×∫_0 ^(π/2) sin^(2n) xdx gamma function... 2∫_0 ^(π/2) sin^(2p−1) xcos^(2q−1) xdx=((⌈(p)⌈(q))/(⌈(p+q))) r×2∫_0 ^(π/2) sin^(2n+1−1) xcos^(2×(1/2)−1) dx =r×((⌈(2n+1)⌈((1/2)))/(⌈(2n+1+(1/2)))) i have tried to solve..others pls check...](Q53718.png)
| ||
Question and Answers Forum | ||
Question Number 53694 by gunawan last updated on 25/Jan/19 | ||
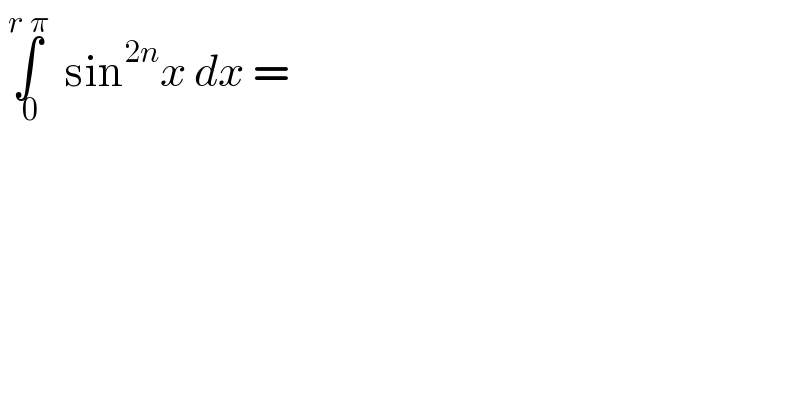 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19 | ||
![∫_0 ^π sinxdx=∣−cosx∣_0 ^π =−(cosπ−cos0)=2 so the area of each loop of f(x)=sinx is 2 f(x)=sin^(2n) x f(rπ−x)=[sin(rπ−x)]^(2n) =[eitther +sinx or −sinx] but [sin(rπ−x)]^(2n) =sin^(2n) x now ∫_0 ^(2a) f(x)dx=2∫_0 ^a f(x)dx when f(2a−x)=f(x) sinx =sin(2π+x) peridocity 2π ∫_0 ^(rπ) sin^(2n) xdx =∫_0 ^((r/2)×2π) sin^(2n) xdx =(r/2)∫_0 ^(2π) sin^(2n) xdx =(r/2)×2∫_0 ^π sin^(2n) xdx[∫_0 ^(2a) f(x)dx=2∫_0 ^a f(x)dx whenf(2a−x)=f(x)] =2r×∫_0 ^(π/2) sin^(2n) xdx gamma function... 2∫_0 ^(π/2) sin^(2p−1) xcos^(2q−1) xdx=((⌈(p)⌈(q))/(⌈(p+q))) r×2∫_0 ^(π/2) sin^(2n+1−1) xcos^(2×(1/2)−1) dx =r×((⌈(2n+1)⌈((1/2)))/(⌈(2n+1+(1/2)))) i have tried to solve..others pls check...](Q53718.png) | ||
| ||