Question Number 53755 by ajfour last updated on 25/Jan/19
Commented by ajfour last updated on 25/Jan/19
$${thanks},\:{how}\:{is}\:{scalene}\:\bigtriangleup\:{area} \\ $$$${obtained}\:? \\ $$
Commented by mr W last updated on 25/Jan/19
Commented by Kunal12588 last updated on 25/Jan/19
$${s}=\frac{{p}+{q}+{q}+{r}+{r}+{p}}{\mathrm{2}}={p}+{q}+{r} \\ $$$$\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\: \\ $$$$=\sqrt{\left({p}+{q}+{r}\right)\left({p}+{q}+{r}−{p}−{q}\right)\left({p}+{q}+{r}−{q}−{r}\right)\left({p}+{q}+{r}−{r}−{p}\right)} \\ $$$$=\sqrt{\left({p}+{q}+{r}\right){pqr}}\:\left({it}\:{seems}\:{to}\:{be}\:{right}\right) \\ $$$${really}\:{cool}\:{si}\overset{} {{r}} \\ $$
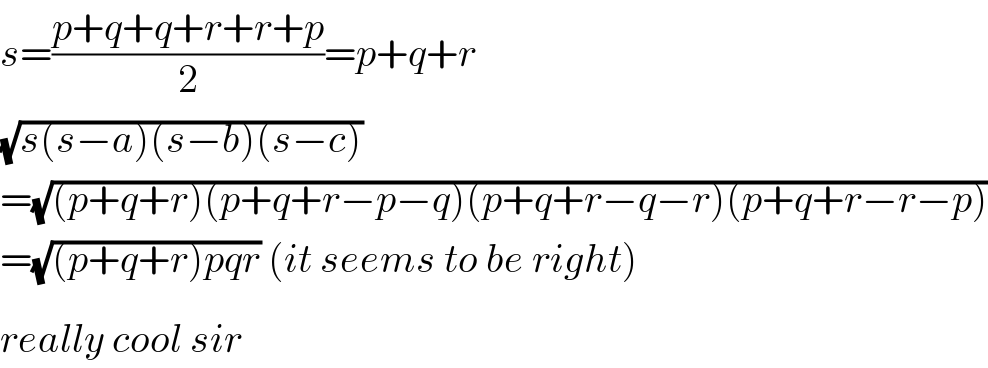
Commented by ajfour last updated on 25/Jan/19
![incidently i found just now that Area(△ABC)=(√((p+q+r)pqr)) but why ? [how to find area of a triangle = (√(s(s−a)(s−b)(s−c))) ?] what i did p+q=c q+r=a r+p=b ⇒ p+q+r = s ⇒ p=s−a , q=s−b , r=s−c Area(△ABC)=(√(s(s−a)(s−b)(s−c))) hence △=(√((p+q+r)pqr)) . but how △=(√(s(s−a)(s−b)(s−c))) if i knew i have forgotten.. please help..](Q53756.png)
$${incidently}\:{i}\:{found}\:{just}\:{now}\:{that} \\ $$$${Area}\left(\bigtriangleup{ABC}\right)=\sqrt{\left({p}+{q}+{r}\right){pqr}} \\ $$$${but}\:{why}\:?\:\left[{how}\:{to}\:{find}\:{area}\:{of}\:{a}\right. \\ $$$$\left.{triangle}\:=\:\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\:\:?\right] \\ $$$${what}\:{i}\:{did} \\ $$$${p}+{q}={c} \\ $$$${q}+{r}={a} \\ $$$${r}+{p}={b} \\ $$$$\Rightarrow\:\:{p}+{q}+{r}\:=\:{s} \\ $$$$\Rightarrow\:{p}={s}−{a}\:,\:{q}={s}−{b}\:,\:{r}={s}−{c} \\ $$$${Area}\left(\bigtriangleup{ABC}\right)=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${hence}\:\:\bigtriangleup=\sqrt{\left({p}+{q}+{r}\right){pqr}}\:\:. \\ $$$${but}\:{how}\:\bigtriangleup=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${if}\:{i}\:{knew}\:{i}\:{have}\:{forgotten}.. \\ $$$${please}\:{help}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
$${area}\:\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}{absinC} \\ $$$${cosC}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$${sinC}=\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\frac{\left(\mathrm{2}{ab}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\left(\mathrm{2}{ab}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right.}{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ab}}×\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({c}+{a}−{b}\right)\left({c}−{a}+{b}\right)}\: \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}{absinC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ab}×\frac{\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({c}+{a}−{b}\right)\left({c}−{a}+{b}\right)}}{\mathrm{2}{ab}} \\ $$$$=\sqrt{\frac{{a}+{b}+{c}}{\mathrm{2}}×\frac{{a}+{b}−{c}}{\mathrm{2}}×\frac{{a}+{c}−{b}}{\mathrm{2}}×\frac{{b}+{c}−{a}}{\mathrm{2}}} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}}\left({assume}\right) \\ $$$$=\sqrt{{s}×\frac{\mathrm{2}{s}−{c}−{c}}{\mathrm{2}}×\frac{\mathrm{2}{s}−{b}−{b}}{\mathrm{2}}×\frac{\mathrm{2}{s}−{a}−{a}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{{s}\left(\mathrm{2}{s}−\mathrm{2}{c}\right)}{\mathrm{2}}×\frac{\mathrm{2}{s}−\mathrm{2}{b}}{\mathrm{2}}×\frac{\mathrm{2}{s}−\mathrm{2}{a}}{\mathrm{2}}}\: \\ $$$$=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\:{Proof} \\ $$
Commented by mr W last updated on 25/Jan/19
![(√(c^2 −h^2 ))+(√(b^2 −h^2 ))=a (√(c^2 −h^2 ))=a−(√(b^2 −h^2 )) c^2 −h^2 =a^2 −2a(√(b^2 −h^2 ))+b^2 −h^2 a^2 +b^2 −c^2 =2a(√(b^2 −h^2 )) (a^2 +b^2 −c^2 )^2 =4a^2 (b^2 −h^2 ) 4a^2 h^2 =(2ab)^2 −(a^2 +b^2 −c^2 )^2 4a^2 h^2 =(2ab+a^2 +b^2 −c^2 )(2ab−a^2 −b^2 +c^2 ) 4a^2 h^2 =[(a+b)^2 −c^2 ][c^2 −(a−b)^2 ] 4a^2 h^2 =(a+b+c)(a+b−c)(c+a−b)(c−a+b) 4a^2 h^2 =(a+b+c)(−a+b+c)(a−b+c)(a+b−c) 4a^2 h^2 =2s(2s−2a)(2s−2b)(2s−2c) a^2 h^2 =4s(s−a)(s−b)(s−c) ⇒h=((2(√(s(s−a)(s−b)(s−c))))/a) Δ=((ah)/2)=(√(s(s−a)(s−b)(s−c)))](Q53762.png)
$$\sqrt{{c}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }={a} \\ $$$$\sqrt{{c}^{\mathrm{2}} −{h}^{\mathrm{2}} }={a}−\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${c}^{\mathrm{2}} −{h}^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2}{a}\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }+{b}^{\mathrm{2}} −{h}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{2}{a}\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} −{h}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left(\mathrm{2}{ab}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left(\mathrm{2}{ab}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\left(\mathrm{2}{ab}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left[\left({a}+{b}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} \right]\left[{c}^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right] \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({c}+{a}−{b}\right)\left({c}−{a}+{b}\right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\mathrm{2}{s}\left(\mathrm{2}{s}−\mathrm{2}{a}\right)\left(\mathrm{2}{s}−\mathrm{2}{b}\right)\left(\mathrm{2}{s}−\mathrm{2}{c}\right) \\ $$$${a}^{\mathrm{2}} {h}^{\mathrm{2}} =\mathrm{4}{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right) \\ $$$$\Rightarrow{h}=\frac{\mathrm{2}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}{{a}} \\ $$$$\Delta=\frac{{ah}}{\mathrm{2}}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$
Commented by Kunal12588 last updated on 25/Jan/19
$${the}\:{formula}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\:{is}\:{called} \\ $$$${Heron}'{s}\:{formula} \\ $$
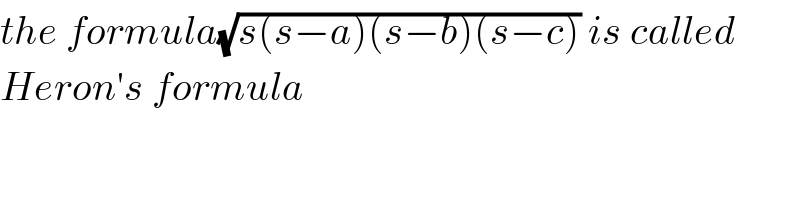
Commented by ajfour last updated on 25/Jan/19
$${Thanks}\:{eveyrone}!\:{but}\:{i}\:{believe} \\ $$$${there}\:{has}\:{to}\:{be}\:{some}\:{more}\:{basic}, \\ $$$${natural}\:{and}\:{symmetrical}\:{way}\:{to} \\ $$$${the}\:{formula}. \\ $$
Commented by peter frank last updated on 25/Jan/19
$${perimeter}\:{of}\:{triangle} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$$\mathrm{2}{s}={a}+{b}+{c} \\ $$$${from} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{ab}\mathrm{sin}\:{c} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{ab}\mathrm{2sin}\:\frac{{c}}{\mathrm{2}}\mathrm{cos}\:\frac{{c}}{\mathrm{2}} \\ $$$${A}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=? \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=? \\ $$$$\mathrm{sin}\:^{\mathrm{2}} {c}=\frac{\mathrm{1}−\mathrm{cos}\:{c}}{\mathrm{2}} \\ $$$${from} \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:{c} \\ $$$$\mathrm{cos}\:{c}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}\right)}{\mathrm{2}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{{c}^{\mathrm{2}} +\mathrm{2}{ab}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{ab}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{{c}^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} }{\mathrm{4}{ab}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} {c}=\frac{\left({a}+{c}−{b}\right)\left({c}−\left({a}−{b}\right)\right.}{\mathrm{4}{ab}} \\ $$$${recall} \\ $$$$\mathrm{2}{s}={a}+{b}+{c} \\ $$$${a}+{c}=\mathrm{2}{s}−{b} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{\left({a}+{c}−{b}\right)\left({c}−\left({a}−{b}\right)\right.}{\mathrm{4}{ab}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{\left({s}−{b}\right)\left({s}−{a}\right)}{{ab}}.....\left({i}\right) \\ $$$${recall} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{cos}\:{c}}{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:{c} \\ $$$$\mathrm{cos}\:{c}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{\mathrm{1}+\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}\right)}{\mathrm{2}} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}−{c}^{\mathrm{2}} }{\mathrm{4}{ab}} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}=\frac{{s}\left({s}−{c}\right)}{{ab}}......\left({ii}\right) \\ $$$${A}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \frac{{c}}{\mathrm{2}} \\ $$$${A}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \frac{\left({s}−{b}\right)\left({s}−{a}\right)}{{ab}}.\frac{{s}\left({s}−{c}\right)}{{ab}} \\ $$$${A}^{\mathrm{2}} ={s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right) \\ $$$${A}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$ \\ $$
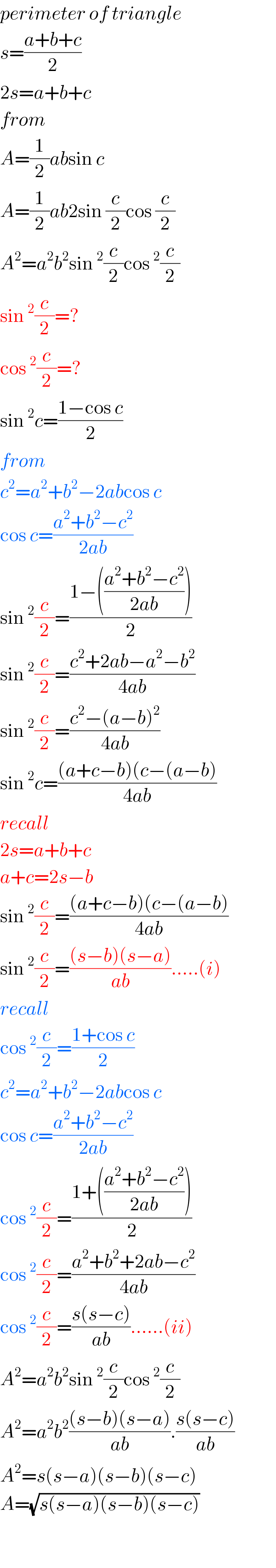
Answered by MJS last updated on 25/Jan/19
$$\mathrm{these}\:\mathrm{things}\:\mathrm{I}\:\mathrm{remember},\:\mathrm{but}\:\mathrm{some}\:\mathrm{further} \\ $$$$\mathrm{steps}\:\mathrm{are}\:\mathrm{missing} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{draw}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{and}\:\mathrm{its}\:\mathrm{incircle}\:\left(\mathrm{center}={I}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{draw}\:\mathrm{the}\:\mathrm{radii}\:\bot\:\mathrm{to}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{which}\:\mathrm{leads} \\ $$$$\:\:\:\:\:\:\:\mathrm{to}\:\mathrm{the}\:\mathrm{points}\:{I}_{{a}} ,\:{I}_{{b}} ,\:{I}_{{c}} \\ $$$$\left(\mathrm{3}\right)\:\mid{AI}_{{b}} \mid=\mid{AI}_{{c}} \mid={i} \\ $$$$\:\:\:\:\:\:\:\mid{BI}_{{a}} \mid=\mid{BI}_{{c}} \mid={j} \\ $$$$\:\:\:\:\:\:\:\mid{CI}_{{a}} \mid=\mid{CI}_{{b}} \mid={k} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:{ABC}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\:\:\:\:\:\:\:\mathrm{of}\:\mathrm{the}\:\mathrm{areas}\:\mathrm{of}\:\mathrm{the}\:\mathrm{6}\:\mathrm{rectangular}\:\mathrm{sub}− \\ $$$$\:\:\:\:\:\:\:\mathrm{triangles}\:\mathrm{we}\:\mathrm{just}\:\mathrm{created}: \\ $$$$\:\:\:\:\:\:\:\bigtriangleup={r}\left({i}+{j}+{k}\right) \\ $$$$\left(\mathrm{5}\right)\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:{ABC}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\:\:\:\:\:\:\:\mathrm{of}\:\mathrm{the}\:\mathrm{three}\:\mathrm{triangles}\:{ABI},\:{BCI},\:{CAI} \\ $$$$\:\:\:\:\:\:\:\bigtriangleup=\frac{{r}}{\mathrm{2}}\left({a}+{b}+{c}\right) \\ $$$$ \\ $$$$\left(\mathrm{6}\right)\:\mathrm{we}\:\mathrm{know} \\ $$$${i}+{j}={c} \\ $$$${i}+{k}={b} \\ $$$${j}+{k}={a} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$$\Rightarrow\:{i}={s}−{a};\:{j}={s}−{b};\:{k}={s}−{c} \\ $$$$ \\ $$$$\mathrm{there}\:\mathrm{was}\:\mathrm{something}\:\mathrm{with}\:\mathrm{the}\:\mathrm{radii}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{excircles}\:\mathrm{to}\:\mathrm{eliminate}\:{r}... \\ $$