
Question and Answers Forum
Question Number 53783 by maxmathsup by imad last updated on 25/Jan/19
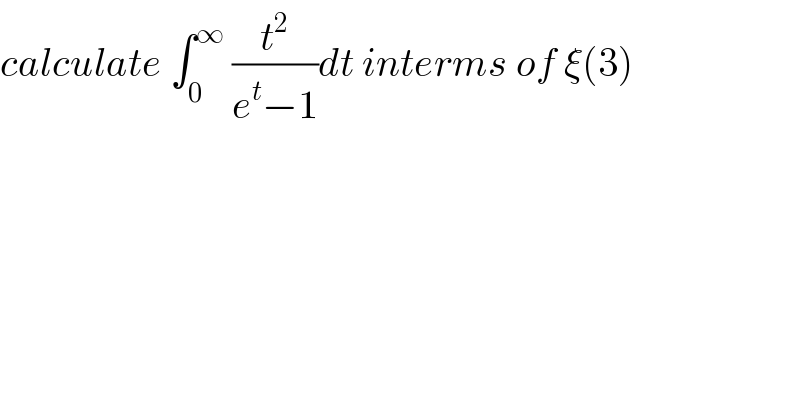
Answered by Smail last updated on 26/Jan/19
![A∫_0 ^∞ (t^2 /(e^t −1))dt=∫_0 ^∞ ((t^2 e^(−t) )/(1−e^(−t) ))dt =∫_0 ^∞ t^2 e^(−t) Σ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^∞ ∫_0 ^∞ t^2 e^(−(n+1)t) dt by parts u=t^2 ⇒u′=2t v′=e^(−(n+1)t) ⇒v=((−1)/(n+1))e^(−(n+1)t) A=Σ_(n=0) ^∞ (2/(n+1))∫_0 ^∞ te^(−(n+1)t) dt with ([t^2 e^(−(n+1)t) ]_0 ^∞ =0) by parts A=Σ_(n=0) ^∞ (2/((n+1)^2 ))∫_0 ^∞ e^(−(n+1)t) dt =Σ_(n=0) ^∞ (2/((n+1)^3 ))[e^(−(n+1)t) ]_0 ^∞ =2Σ_(n=0) ^∞ (1/((n+1)^3 )) =2Σ_(n=1) ^∞ (1/n^3 )=2ξ(3)](Q53798.png)
Commented by maxmathsup by imad last updated on 26/Jan/19

| ||
Question and Answers Forum | ||
Question Number 53783 by maxmathsup by imad last updated on 25/Jan/19 | ||
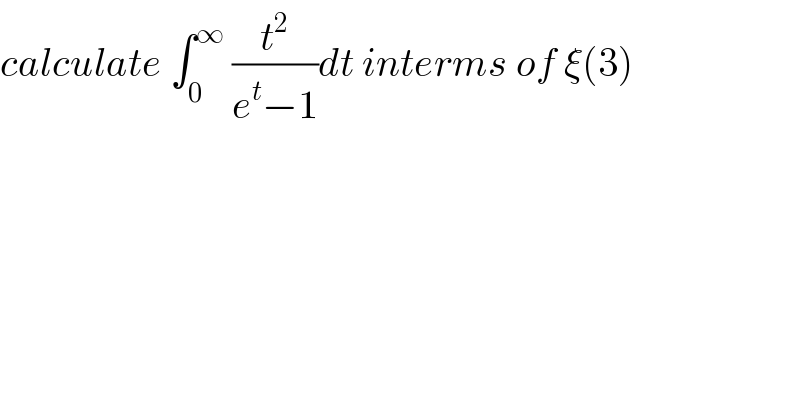 | ||
Answered by Smail last updated on 26/Jan/19 | ||
![A∫_0 ^∞ (t^2 /(e^t −1))dt=∫_0 ^∞ ((t^2 e^(−t) )/(1−e^(−t) ))dt =∫_0 ^∞ t^2 e^(−t) Σ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^∞ ∫_0 ^∞ t^2 e^(−(n+1)t) dt by parts u=t^2 ⇒u′=2t v′=e^(−(n+1)t) ⇒v=((−1)/(n+1))e^(−(n+1)t) A=Σ_(n=0) ^∞ (2/(n+1))∫_0 ^∞ te^(−(n+1)t) dt with ([t^2 e^(−(n+1)t) ]_0 ^∞ =0) by parts A=Σ_(n=0) ^∞ (2/((n+1)^2 ))∫_0 ^∞ e^(−(n+1)t) dt =Σ_(n=0) ^∞ (2/((n+1)^3 ))[e^(−(n+1)t) ]_0 ^∞ =2Σ_(n=0) ^∞ (1/((n+1)^3 )) =2Σ_(n=1) ^∞ (1/n^3 )=2ξ(3)](Q53798.png) | ||
| ||
Commented by maxmathsup by imad last updated on 26/Jan/19 | ||
 | ||