calculate Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =1−(1/5) +(1/9) −(1/(13)) +....


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 53795 by maxmathsup by imad last updated on 25/Jan/19

$c a l c u l a t e \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{4 n + 1} = 1 - \frac{1}{5} + \frac{1}{9} - \frac{1}{13} + . . . .$
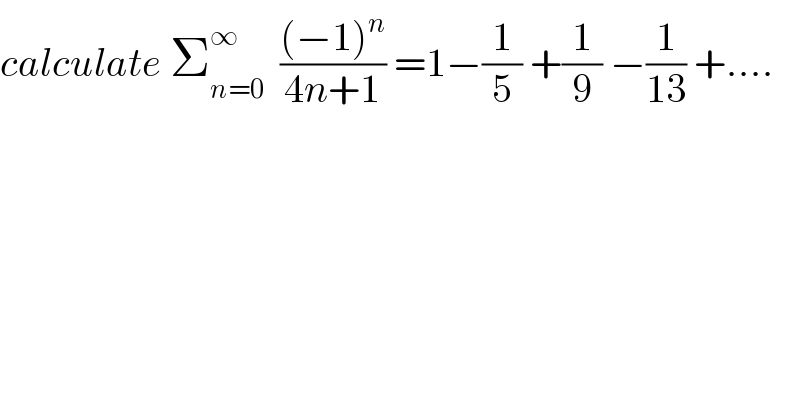
Commented by maxmathsup by imad last updated on 26/Jan/19
$let S(x)=Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) x^(4n+1) with∣x∣<1 due to uniform convergence we have (d/dx)S(x) =Σ_(n=0) ^∞ (−1)^n x^(4n) =Σ_(n=0) ^∞ (−x^4 )^n =(1/(1+x^4 )) ⇒S(x)=∫_0 ^x (dt/(t^4 +1)) +c c=S(0)=0 ⇒S(x)=∫_0 ^x (dt/(t^4 +1)) and Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =S(1)=∫_0 ^1 (dt/(t^4 +1)) let decompose F(t) =(1/(t^4 +1)) ⇒ F(t)=(1/((t^2 +1)^2 −2t^2 )) =(1/((t^2 +(√2)t +1)(t^2 −(√2)t +1))) =((at+b)/(t^2 +(√2)t +1)) +((ct +d)/(t^2 −(√2)t +1)) F(−t) =F(t) ⇒((−at +b)/(t^2 −(√2)t +1)) +((−bt +c)/(t^2 +(√2)t +1)) =F(t) ⇒c=−a and d=b ⇒ F(t) =((at +b)/(t^2 +(√2)t +1)) +((−at +b)/(t^2 −(√2)t +1)) F(0) =1 =2b ⇒b =(1/2) F(1) =(1/2) =((a +b)/(2+(√2))) +((−a+b)/(2−(√2))) ⇒ (1/2) =(((2−(√2))(a+(1/2))+(2+(√2))(−a+(1/2)))/2) ⇒ −2(√2)a +(1/(2 ))(4) =1 ⇒ −2(√2)a =−1 ⇒a =(1/(2(√2))) ⇒ F(t) = (((t/(2(√2)))+(1/2))/(t^2 +(√2)t +1)) +((−(t/(2(√2)))+(1/2))/(t^2 −(√2)t +1)) =(1/(2(√2))){ ((t+(√2))/(t^2 +(√2)t +1)) +((−t +(√2))/(t^2 −(√2)t +1))} ⇒ ∫_0 ^1 (dt/(t^4 +1)) =((√2)/4){ ∫_0 ^1 ((t+(√2))/(t^2 +(√2)t +1))dt − ∫_0 ^1 ((t−(√2))/(t^2 −(√2)t +1))} =((√2)/4){ (1/2) ∫_0 ^1 ((2t +(√2) +(√2))/(t^2 +(√2)t +1)) dt −(1/2)∫_0 ^1 ((2t−(√2)−(√2))/(t^2 −(√2)t +1)) dt} =((√2)/8){ [ln(t^2 +(√2)t +1)]_0 ^1 −[ln(t^2 −(√2)t +1)]_0 ^1 +(√2)∫_0 ^1 (dt/(t^2 +(√2)t +1)) +(√2)∫_0 ^1 (dt/(t^2 −(√2)t +1))} =((√2)/8){ ln(2+(√2))−ln(2−(√2))} +(1/4){ ∫_0 ^1 (dt/(t^2 +(√2)t +1)) +∫_0 ^1 (dt/(t^2 −(√2)t +1))} but ∫_0 ^1 (dt/(t^2 +(√2)t +1)) = ∫_0 ^1 (dt/(t^2 +2 ((√2)/2)t +(1/2)+(1/2))) =∫_0 ^1 (dt/((t+(1/(√2)))^2 +(1/2))) =_(t +(1/(√2))=(u/(√2))) ∫_1 ^(1+(√2)) (du/((√2)(1/2)(1+u^2 ))) =(√2) ∫_1 ^(1+(√2)) (du/u) =(√2){arctan((√2)+1)−(π/4)} ∫_0 ^1 (dt/(t^2 −(√2)t +1)) = ∫_0 ^1 (dt/((t−(1/(√2)))^2 +(1/2))) =_(t−(1/(√2))=(u/(√2))) ∫_(−1) ^((√2)−1) (du/((√2)(1/2)(1+u^2 ))) =(√2){arctan((√2)−1) +(π/4)} ⇒ ∫_0 ^1 (dt/(t^4 +1)) =((√2)/8)ln(((2+(√2))/(2−(√2)))) +((√2)/4){ arctan((√2)+1) +arctan((√2)−1)} but arctan((√2)−1) =arctan( (1/((√2)+1)))=(π/2) −arctan((√2)+1) ⇒ ∫_0 ^1 (dt/(t^4 +1)) =((√2)/8)ln(((2+(√2))/(2−(√2)))) +((π(√2))/8) ⇒ Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =((√2)/8)ln(((2+(√2))/(2−(√2))))+((π(√2))/8) .$
$l e t S (x) = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{4 n + 1} x^{4 n + 1} w i t h ∣ x ∣< 1 d u e t o u n i f o r m c o n v e r g e n c e w e h a v e$ $\frac{d}{d x} S (x) = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{4 n} = \sum_{n = 0}^{\infty} {(- x^{4})}^{n} = \frac{1}{1 + x^{4}} \Rightarrow S (x) = \int_{0}^{x} \frac{d t}{t^{4} + 1} + c$ $c = S (0) = 0 \Rightarrow S (x) = \int_{0}^{x} \frac{d t}{t^{4} + 1} a n d \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{4 n + 1} = S (1) = \int_{0}^{1} \frac{d t}{t^{4} + 1}$ $l e t d e c o m p o s e F (t) = \frac{1}{t^{4} + 1} \Rightarrow F (t) = \frac{1}{{(t^{2} + 1)}^{2} - 2 t^{2}} = \frac{1}{(t^{2} + \sqrt{2} t + 1) (t^{2} - \sqrt{2} t + 1)}$ $= \frac{a t + b}{t^{2} + \sqrt{2} t + 1} + \frac{c t + d}{t^{2} - \sqrt{2} t + 1}$ $F (- t) = F (t) \Rightarrow \frac{- a t + b}{t^{2} - \sqrt{2} t + 1} + \frac{- b t + c}{t^{2} + \sqrt{2} t + 1} = F (t) \Rightarrow c = - a a n d d = b \Rightarrow$ $F (t) = \frac{a t + b}{t^{2} + \sqrt{2} t + 1} + \frac{- a t + b}{t^{2} - \sqrt{2} t + 1}$ $F (0) = 1 = 2 b \Rightarrow b = \frac{1}{2}$ $F (1) = \frac{1}{2} = \frac{a + b}{2 + \sqrt{2}} + \frac{- a + b}{2 - \sqrt{2}} \Rightarrow \frac{1}{2} = \frac{(2 - \sqrt{2}) (a + \frac{1}{2}) + (2 + \sqrt{2}) (- a + \frac{1}{2})}{2} \Rightarrow$ $- 2 \sqrt{2} a + \frac{1}{2} (4) = 1 \Rightarrow - 2 \sqrt{2} a = - 1 \Rightarrow a = \frac{1}{2 \sqrt{2}} \Rightarrow$ $F (t) = \frac{\frac{t}{2 \sqrt{2}} + \frac{1}{2}}{t^{2} + \sqrt{2} t + 1} + \frac{- \frac{t}{2 \sqrt{2}} + \frac{1}{2}}{t^{2} - \sqrt{2} t + 1} = \frac{1}{2 \sqrt{2}} {\frac{t + \sqrt{2}}{t^{2} + \sqrt{2} t + 1} + \frac{- t + \sqrt{2}}{t^{2} - \sqrt{2} t + 1}} \Rightarrow$ $\int_{0}^{1} \frac{d t}{t^{4} + 1} = \frac{\sqrt{2}}{4} {\int_{0}^{1} \frac{t + \sqrt{2}}{t^{2} + \sqrt{2} t + 1} d t - \int_{0}^{1} \frac{t - \sqrt{2}}{t^{2} - \sqrt{2} t + 1}}$ $= \frac{\sqrt{2}}{4} {\frac{1}{2} \int_{0}^{1} \frac{2 t + \sqrt{2} + \sqrt{2}}{t^{2} + \sqrt{2} t + 1} d t - \frac{1}{2} \int_{0}^{1} \frac{2 t - \sqrt{2} - \sqrt{2}}{t^{2} - \sqrt{2} t + 1} d t}$ $= \frac{\sqrt{2}}{8} {{[l n (t^{2} + \sqrt{2} t + 1)]}_{0}^{1} - {[l n (t^{2} - \sqrt{2} t + 1)]}_{0}^{1} + \sqrt{2} \int_{0}^{1} \frac{d t}{t^{2} + \sqrt{2} t + 1}$ $+ \sqrt{2} \int_{0}^{1} \frac{d t}{t^{2} - \sqrt{2} t + 1}}$ $= \frac{\sqrt{2}}{8} {l n (2 + \sqrt{2}) - l n (2 - \sqrt{2})} + \frac{1}{4} {\int_{0}^{1} \frac{d t}{t^{2} + \sqrt{2} t + 1} + \int_{0}^{1} \frac{d t}{t^{2} - \sqrt{2} t + 1}} b u t$ $\int_{0}^{1} \frac{d t}{t^{2} + \sqrt{2} t + 1} = \int_{0}^{1} \frac{d t}{t^{2} + 2 \frac{\sqrt{2}}{2} t + \frac{1}{2} + \frac{1}{2}} = \int_{0}^{1} \frac{d t}{{(t + \frac{1}{\sqrt{2}})}^{2} + \frac{1}{2}}$ $=_{t + \frac{1}{\sqrt{2}} = \frac{u}{\sqrt{2}}} \int_{1}^{1 + \sqrt{2}} \frac{d u}{\sqrt{2} \frac{1}{2} (1 + u^{2})} = \sqrt{2} \int_{1}^{1 + \sqrt{2}} \frac{d u}{u} = \sqrt{2} {a r c t a n (\sqrt{2} + 1) - \frac{π}{4}}$ $\int_{0}^{1} \frac{d t}{t^{2} - \sqrt{2} t + 1} = \int_{0}^{1} \frac{d t}{{(t - \frac{1}{\sqrt{2}})}^{2} + \frac{1}{2}} =_{t - \frac{1}{\sqrt{2}} = \frac{u}{\sqrt{2}}} \int_{- 1}^{\sqrt{2} - 1} \frac{d u}{\sqrt{2} \frac{1}{2} (1 + u^{2})}$ $= \sqrt{2} {a r c t a n (\sqrt{2} - 1) + \frac{π}{4}} \Rightarrow$ $\int_{0}^{1} \frac{d t}{t^{4} + 1} = \frac{\sqrt{2}}{8} l n (\frac{2 + \sqrt{2}}{2 - \sqrt{2}}) + \frac{\sqrt{2}}{4} {a r c t a n (\sqrt{2} + 1) + a r c t a n (\sqrt{2} - 1)} b u t$ $a r c t a n (\sqrt{2} - 1) = a r c t a n (\frac{1}{\sqrt{2} + 1}) = \frac{π}{2} - a r c t a n (\sqrt{2} + 1) \Rightarrow$ $\int_{0}^{1} \frac{d t}{t^{4} + 1} = \frac{\sqrt{2}}{8} l n (\frac{2 + \sqrt{2}}{2 - \sqrt{2}}) + \frac{π \sqrt{2}}{8} \Rightarrow \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{4 n + 1} = \frac{\sqrt{2}}{8} l n (\frac{2 + \sqrt{2}}{2 - \sqrt{2}}) + \frac{π \sqrt{2}}{8} .$
	Answered by Smail last updated on 26/Jan/19

	$\frac{1}{1 - x} = \underset{n = 0}{\sum^{\infty}} x^{n}$ $S o \frac{1}{1 + x^{4}} = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} x^{4 n}$ $l e t p (x) = \int_{0}^{x} \frac{d t}{1 + t^{4}} = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} \int_{0}^{x} t^{4 n} d t = \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n}}{4 n + 1} x^{4 n + 1}$ $p (1) = \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n}}{4 n + 1}$ $p (x) = \int_{0}^{x} \frac{d t}{1 + t^{4}} = \int_{0}^{x} \frac{d t}{(t^{2} + \sqrt{2} t + 1) (t^{2} - \sqrt{2} t + 1)}$ $\frac{1}{1 + t^{4}} = \frac{a t + b}{t^{2} + \sqrt{2} t + 1} + \frac{c t + d}{t^{2} - \sqrt{2} t + 1}$ $a = - c = \frac{\sqrt{2}}{4}; d = b = \frac{1}{2}$ $p (x) = \frac{\sqrt{2}}{4} \int_{0}^{x} (\frac{t + \sqrt{2}}{t^{2} + \sqrt{2} t + 1} - \frac{t - \sqrt{2}}{t^{2} - \sqrt{2} t + 1}) d t$ $p (1) = \frac{\sqrt{2}}{2} \int_{0}^{1} (\frac{t + \sqrt{2}}{{(\sqrt{2} t + 1)}^{2} + 1} - \frac{t - \sqrt{2}}{{(\sqrt{2} t - 1)}^{2} + 1}) d t$ $u = \sqrt{2} t + 1 \Rightarrow d u = \sqrt{2} d t$ $y = \sqrt{2} t - 1 \Rightarrow d y = \sqrt{2} d t$ $p (1) = \frac{\sqrt{2}}{4} (\int_{1}^{\sqrt{2} + 1} \frac{u + 1}{u^{2} + 1} d y - \int_{- 1}^{\sqrt{2} - 1} \frac{y - 1}{y^{2} + 1} d y)$ $= \frac{\sqrt{2}}{4} ({[\frac{1}{2} l n (u^{2} + 1) + {t a n}^{- 1} (u)]}_{1}^{\sqrt{2} + 1} - {[\frac{1}{2} l n (y^{2} + 1) - {t a n}^{- 1} (y)]}_{- 1}^{\sqrt{2} - 1})$ $= \frac{\sqrt{2}}{4} (\frac{1}{4} l n 2 + \frac{1}{2} l n (\sqrt{2} + 1) + {t a n}^{- 1} (\sqrt{2} + 1) - \frac{π}{4} - (\frac{1}{4} l n (2) + \frac{1}{2} l n (\sqrt{2} - 1) - {t a n}^{- 1} (\sqrt{2} - 1) - \frac{π}{4}))$ $= \frac{\sqrt{2}}{4} (l n (\sqrt{2} + 1) + {t a n}^{- 1} (\sqrt{2} + 1) + {t a n}^{- 1} (\sqrt{2} - 1))$ $= \frac{\sqrt{2}}{4} (l n (\sqrt{2} + 1) + \frac{3 π}{8} + \frac{π}{8})$ $\underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n}}{4 n + 1} = p (1) = \frac{\sqrt{2}}{4} (l n (\sqrt{2} + 1) + \frac{π}{2})$
	Commented by maxmathsup by imad last updated on 26/Jan/19

	$t h a n k y o u s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum