Question and Answers Forum
Question Number 53910 by ajfour last updated on 27/Jan/19
Commented by ajfour last updated on 27/Jan/19
Commented by ajfour last updated on 27/Jan/19
Commented by ajfour last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19
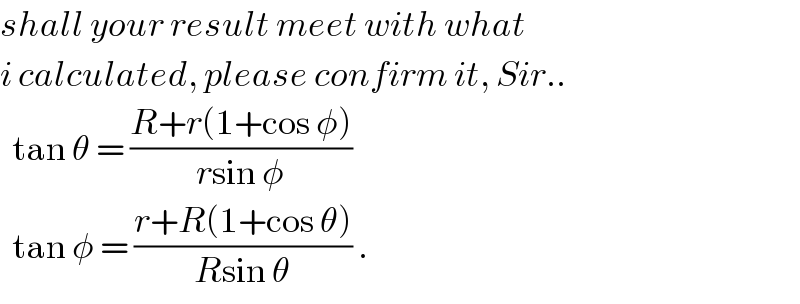
Commented by mr W last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19
Commented by mr W last updated on 27/Jan/19
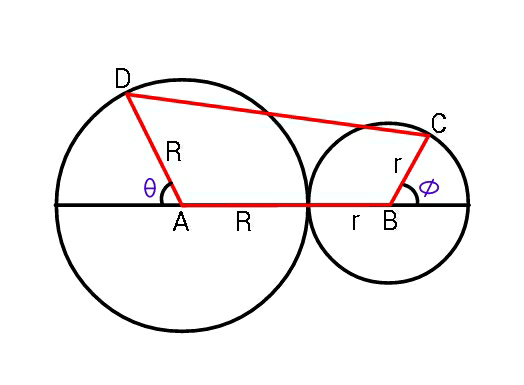
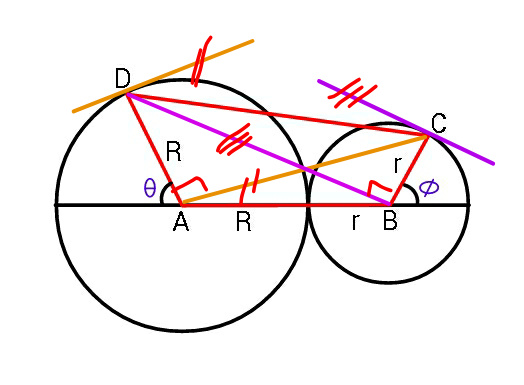
![∠BAC=(π/2)−θ [R+r(1+cos φ)]tan ((π/2)−θ)=r sin φ ⇒tan θ=((R+r(1+cos φ))/(r sin φ)) similarly: [r+R(1+cos θ)]tan ((π/2)−φ)=R sin θ ⇒tan φ=((r+R(1+cos θ))/(R sin θ))](Q53938.png)
Commented by mr W last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19
Commented by ajfour last updated on 28/Jan/19

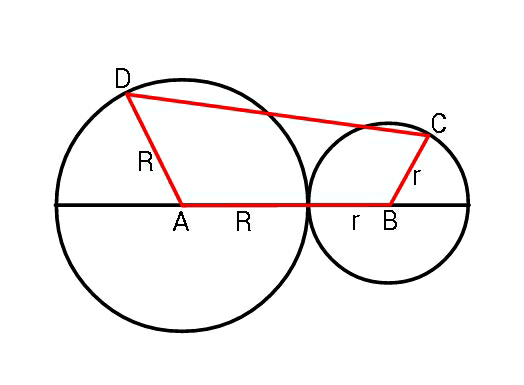
Answered by ajfour last updated on 27/Jan/19
Commented by ajfour last updated on 27/Jan/19
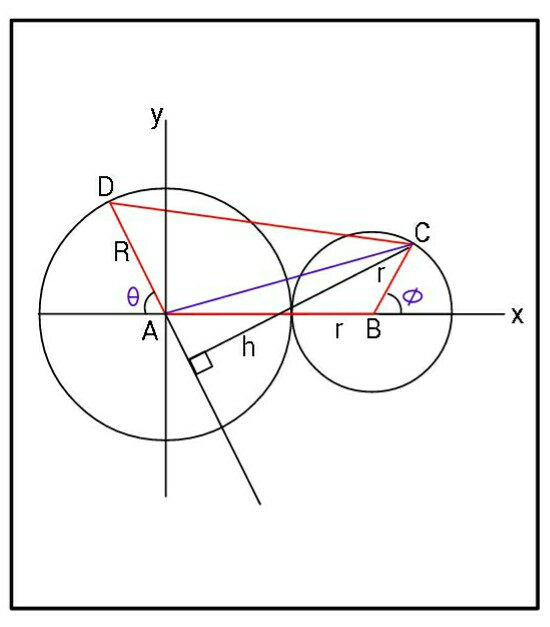
![C(R+r+rcos φ, rsin φ) A=Area(△ABC)+Area(△ACD) A=(((R+r)/2))rsin φ+((Rh)/2) Eq. of AD: y=−xtan θ h=[rsin φ+(R+r+rcos φ)tan θ]cos θ =rsin φcos θ+(R+r+rcos φ)sin θ = (R+r)sin θ+rsin (θ+φ) 2A=(R+r)rsin φ+R(R+r)sin θ +Rrsin (θ+φ) let μ=(R/r) ⇒ 2A/r^2 =(μ+1)sin φ+μ(1+μ)sin θ +μsin (θ+φ) ((2A)/((μ+1)r^2 ))=sin φ+μsin θ+λsin (θ+φ) where λ=(μ/(μ+1)) =(R/(R+r)) ((2/((μ+1)r^2 )))((∂(A))/∂θ)=μcos θ+λcos (θ+φ)=0 ⇒ μcos θ = −λcos (θ+φ) ...(i) ((2/((μ+1)r^2 )))((∂(A))/∂φ)= cos φ+λcos (θ+φ)=0 ⇒ cos φ = −λcos (θ+φ) ...(ii) ⇒ cos φ = μcos θ Now using (i) with μ/λ = b=μ+1 bcos θ+cos θcos φ−sin θsin φ=0 cos^2 θ(b+μcos θ)^2 =(1−cos^2 θ)(1−μ^2 cos^2 θ) let cos θ= z ⇒ b^2 z^2 +2μbz^3 =1−μ^2 z^2 −z^2 but b=μ+1 , ⇒ 2(μ^2 +μ+1)z^2 +2μ(μ+1)z^3 −1=0 ⇒ (1/z^3 )−2(μ^2 +μ+1)(1/z)−2μ(μ+1)=0 (1/z)=(1/(cos θ))=sec θ = t ⇒ t^3 +pt+q =0 with p=−2(μ^2 +μ+1) ; q=−2μ(μ+1) (q^2 /4)+(p^3 /(27)) = μ^2 (μ+1)^2 −((8(μ^2 +μ+1)^3 )/(27)) D < 0 perhaps (as μ>1) ....](Q53940.png)
Commented by ajfour last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19
Commented by mr W last updated on 28/Jan/19
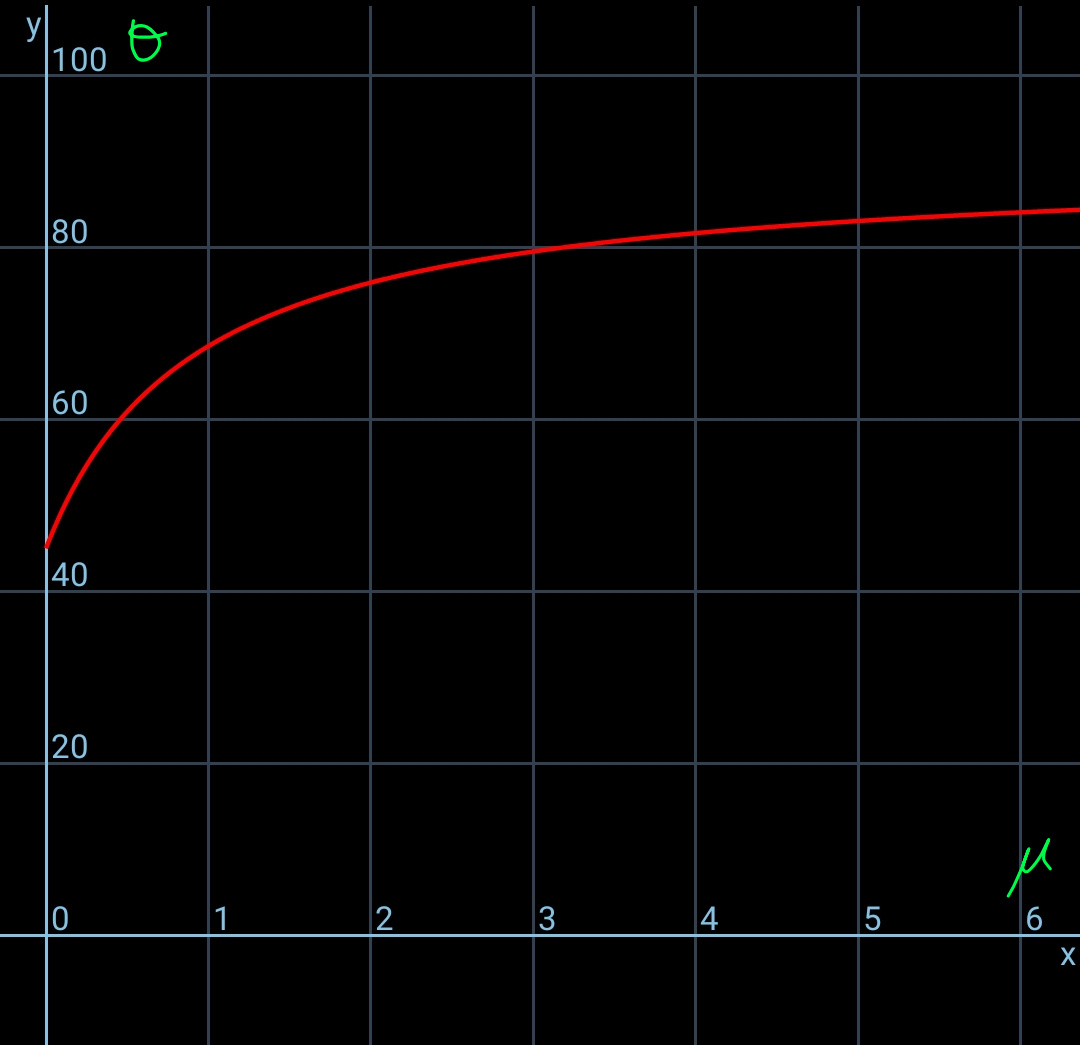
![t^3 −pt−q =0 with p=2(μ^2 +μ+1) ; q=2μ(μ+1) (u+v)^3 −3uv(u+v)−(u^3 +v^3 )=0 let t=u+v u^3 v^3 =((p/3))^3 =(8/(27))(μ^2 +μ+1)^3 u^3 +v^3 =q=2μ(μ+1) u^3 and v^3 are roots of x^2 −2μ(μ+1)x+(8/(27))(μ^2 +μ+1)^3 =0 D=4[μ^2 (μ+1)^2 −(8/(27))(μ^2 +μ+1)^3 ]<0 u^3 (v^3 )=μ(μ+1)±i(√((8/(27))(μ^2 +μ+1)^3 −μ^2 (μ+1)^2 ))=A±iB with A=μ(μ+1), B=(√((8/(27))(μ^2 +μ+1)^3 −μ^2 (μ+1)^2 )) A+iB=(√(A^2 +B^2 ))((A/(√(A^2 +B^2 )))+i(B/(√(A^2 +B^2 ))))=(√(A^2 +B^2 ))(cos α+i sin α) with α=tan^(−1) (B/A)=tan^(−1) (√(((8(μ^2 +μ+1)^3 )/(27μ^2 (μ+1)^2 ))−1)) A^2 +B^2 =(8/(27))(μ^2 +μ+1)^3 u^3 (v^3 )=(√(A^2 +B^2 ))(cos α±i sin α) ⇒u=((A^2 +B^2 ))^(1/6) [cos (((α+2nπ)/3))+i sin (((α+2nπ)/3))] ⇒v=((A^2 +B^2 ))^(1/6) [cos (((α+2nπ)/3))−i sin (((α+2nπ)/3))] ⇒t=u+v=2((A^2 +B^2 ))^(1/6) cos (((α+2nπ)/3)), n=0,1,2 ⇒t=sec θ=2(√((2(μ^2 +μ+1))/3)) cos ((1/3)tan^(−1) (√(((8(μ^2 +μ+1)^3 )/(27μ^2 (μ+1)^2 ))−1)))](Q53975.png)
Commented by ajfour last updated on 27/Jan/19
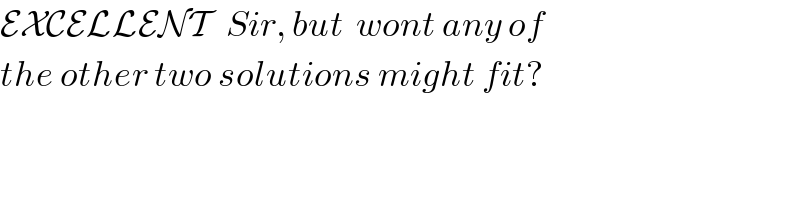
Commented by mr W last updated on 27/Jan/19
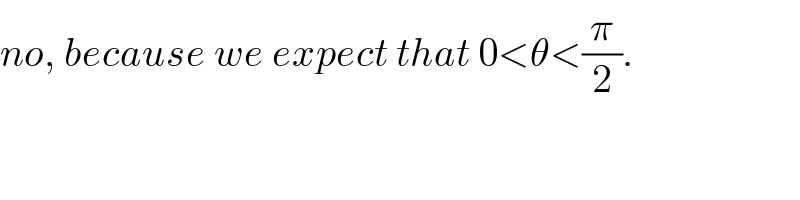
Commented by mr W last updated on 27/Jan/19