
Question and Answers Forum
Question Number 53966 by maxmathsup by imad last updated on 27/Jan/19
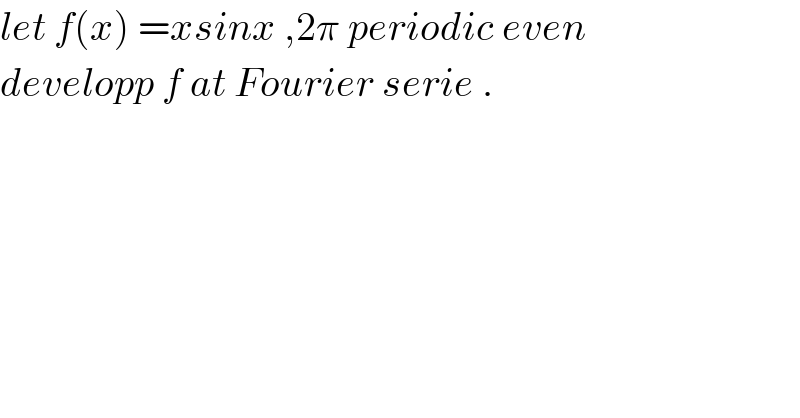
Commented by maxmathsup by imad last updated on 30/Jan/19
![f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) and a_n =(2/T) ∫_([T]) f(x) cos(nx)dx =(2/(2π)) ∫_(−π) ^π xsin(x) cos(nx)dx =(2/π) ∫_0 ^π x sin(x)cos(nx) dx but sin(a+b) =sina cosb +cosa sinb sin(a−b)=sina cosb −cosa sinb ⇒sina cosb=(1/2){sin(a+b)+sin(a−b)} ⇒ (π/2) a_n =(1/2) ∫_0 ^π x{sin(n+1)x−sin(n−1)x}dx ⇒ π a_n =∫_0 ^π x sin(n+1)x dx −∫_0 ^π x sin(n−1)xdx let find I=∫_0 ^π x sin(αx)dx by parts I =[−(x/α)cos(αx)]_0 ^π −∫_0 ^π −(1/α) cos(αx)dx =−(1/α)[ xcos(αx)]_0 ^π +(1/α)[(1/α)sin(αx)]_0 ^π =−(π/α) cos(πα) +(1/α^2 ) sin(απ) ⇒ πa_n =−(π/(n+1))(−1)^(n+1) −(−(π/(n−1))(−1)^(n−1) ) =((π(−1)^n )/(n+1)) −((π(−1)^n )/(n−1)) =π(−1)^n {(1/(n+1)) −(1/(n−1))} =((−2π(−1)^n )/(n^2 −1)) =((2π(−1)^(n−1) )/(n^2 −1)) with n≥2 a_0 =(2/π) ∫_0 ^π xsin(x)dx =(2/π){π}=2 ⇒(a_0 /2) =1 (π/2) a_1 =∫_0 ^π xsin(2x)dx =−(π/2) ⇒a_1 =−1 ⇒ xsin(x) =2Σ_(n=2) ^∞ (((−1)^(n−1) )/(n^2 −1)) cos(nx).](Q54204.png)
| ||
Question and Answers Forum | ||
Question Number 53966 by maxmathsup by imad last updated on 27/Jan/19 | ||
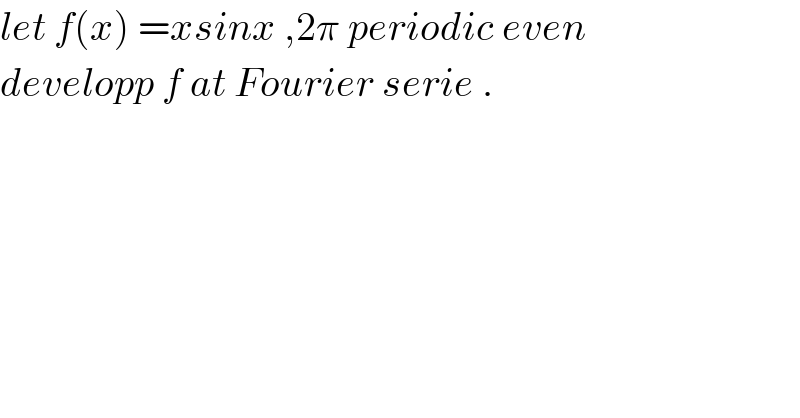 | ||
Commented by maxmathsup by imad last updated on 30/Jan/19 | ||
![f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) and a_n =(2/T) ∫_([T]) f(x) cos(nx)dx =(2/(2π)) ∫_(−π) ^π xsin(x) cos(nx)dx =(2/π) ∫_0 ^π x sin(x)cos(nx) dx but sin(a+b) =sina cosb +cosa sinb sin(a−b)=sina cosb −cosa sinb ⇒sina cosb=(1/2){sin(a+b)+sin(a−b)} ⇒ (π/2) a_n =(1/2) ∫_0 ^π x{sin(n+1)x−sin(n−1)x}dx ⇒ π a_n =∫_0 ^π x sin(n+1)x dx −∫_0 ^π x sin(n−1)xdx let find I=∫_0 ^π x sin(αx)dx by parts I =[−(x/α)cos(αx)]_0 ^π −∫_0 ^π −(1/α) cos(αx)dx =−(1/α)[ xcos(αx)]_0 ^π +(1/α)[(1/α)sin(αx)]_0 ^π =−(π/α) cos(πα) +(1/α^2 ) sin(απ) ⇒ πa_n =−(π/(n+1))(−1)^(n+1) −(−(π/(n−1))(−1)^(n−1) ) =((π(−1)^n )/(n+1)) −((π(−1)^n )/(n−1)) =π(−1)^n {(1/(n+1)) −(1/(n−1))} =((−2π(−1)^n )/(n^2 −1)) =((2π(−1)^(n−1) )/(n^2 −1)) with n≥2 a_0 =(2/π) ∫_0 ^π xsin(x)dx =(2/π){π}=2 ⇒(a_0 /2) =1 (π/2) a_1 =∫_0 ^π xsin(2x)dx =−(π/2) ⇒a_1 =−1 ⇒ xsin(x) =2Σ_(n=2) ^∞ (((−1)^(n−1) )/(n^2 −1)) cos(nx).](Q54204.png) | ||