∫_( 0) ^1 (√((1−x)/(1+x))) dx =


Question and Answers Forum

All Questions Topic List
UNKNOWN Questions
Previous in All Question Next in All Question
Previous in UNKNOWN Next in UNKNOWN
Question Number 54033 by qw last updated on 28/Jan/19

$\underset{0}{\int^{1}} \sqrt{\frac{1 - x}{1 + x}} d x =$
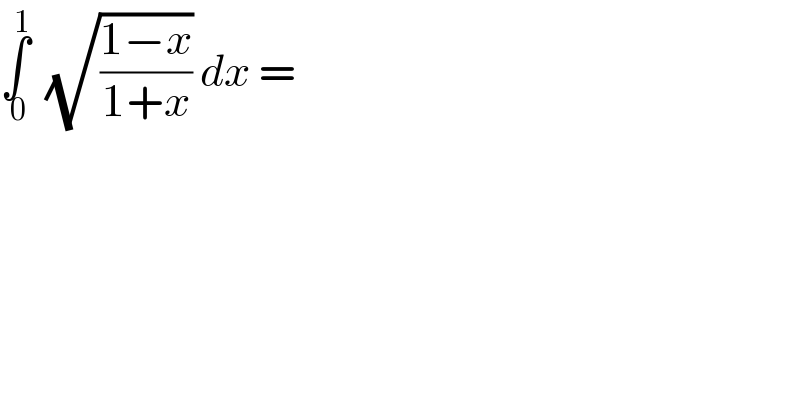
Commented by maxmathsup by imad last updated on 29/Jan/19
$let I =∫_0 ^1 (√((1−x)/(1+x)))dx let use the chan. (√((1−x)/(1+x)))=t ⇒((1−x)/(1+x)) =t^2 ⇒ 1−x =t^2 +t^2 x ⇒1−t^2 =(1+t^2 )x ⇒x =((1−t^2 )/(1+t^2 )) ⇒ (dx/dt) =((−2t(1+t^2 )−(1−t^2 )(2t))/((1+t^2 )^2 )) =((−2t−2t^3 −2t +2t^3 )/((1+t^2 )^2 )) =((−4t)/((1+t^2 )^2 )) ⇒ I = −∫_0 ^1 t(((−4t)/((1+t^2 )^2 )) )dt =4 ∫_0 ^1 (t^2 /((1+t^2 )^2 )) dt =4{ ∫_0 ^1 ((1+t^2 −1)/((1+t^2 )^2 ))dt}=4{∫_0 ^1 (dt/(1+t^2 )) −∫_0 ^1 (dt/((1+t^2 )^2 ))} but ∫_0 ^1 (dt/(1+t^2 )) =[arctant]_0 ^1 =(π/4) ∫_0 ^1 (dt/((1+t^2 )^2 )) =_(t =tanθ) ∫_0 ^(π/4) (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ = ∫_0 ^(π/4) (dθ/(1+tan^2 θ)) =∫_0 ^(π/4) cos^2 θ dθ =∫_0 ^(π/4) ((1+cos(2θ))/2) dθ =(π/8) +(1/4)[sin(2θ)]_0 ^(π/4) =(π/8) +(1/4) ⇒ I =4{(π/4) −(π/8) −(1/4)} =π−(π/2) −1 =(π/2) −1 .$
$l e t I = \int_{0}^{1} \sqrt{\frac{1 - x}{1 + x}} d x l e t u s e t h e c h a n . \sqrt{\frac{1 - x}{1 + x}} = t \Rightarrow \frac{1 - x}{1 + x} = t^{2} \Rightarrow$ $1 - x = t^{2} + t^{2} x \Rightarrow 1 - t^{2} = (1 + t^{2}) x \Rightarrow x = \frac{1 - t^{2}}{1 + t^{2}} \Rightarrow \frac{d x}{d t} = \frac{- 2 t (1 + t^{2}) - (1 - t^{2}) (2 t)}{{(1 + t^{2})}^{2}}$ $= \frac{- 2 t - 2 t^{3} - 2 t + 2 t^{3}}{{(1 + t^{2})}^{2}} = \frac{- 4 t}{{(1 + t^{2})}^{2}} \Rightarrow I = - \int_{0}^{1} t (\frac{- 4 t}{{(1 + t^{2})}^{2}}) d t$ $= 4 \int_{0}^{1} \frac{t^{2}}{{(1 + t^{2})}^{2}} d t = 4 {\int_{0}^{1} \frac{1 + t^{2} - 1}{{(1 + t^{2})}^{2}} d t} = 4 {\int_{0}^{1} \frac{d t}{1 + t^{2}} - \int_{0}^{1} \frac{d t}{{(1 + t^{2})}^{2}}} b u t$ $\int_{0}^{1} \frac{d t}{1 + t^{2}} = {[a r c t a n t]}_{0}^{1} = \frac{π}{4}$ $\int_{0}^{1} \frac{d t}{{(1 + t^{2})}^{2}} =_{t = t a n θ} \int_{0}^{\frac{π}{4}} \frac{(1 + {t a n}^{2} θ)}{{(1 + {t a n}^{2} θ)}^{2}} d θ = \int_{0}^{\frac{π}{4}} \frac{d θ}{1 + {t a n}^{2} θ}$ $= \int_{0}^{\frac{π}{4}} {c o s}^{2} θ d θ = \int_{0}^{\frac{π}{4}} \frac{1 + c o s (2 θ)}{2} d θ = \frac{π}{8} + \frac{1}{4} {[s i n (2 θ)]}_{0}^{\frac{π}{4}} = \frac{π}{8} + \frac{1}{4} \Rightarrow$ $I = 4 {\frac{π}{4} - \frac{π}{8} - \frac{1}{4}} = π - \frac{π}{2} - 1 = \frac{π}{2} - 1 .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19

	$\int \frac{\sqrt{1 - x}}{\sqrt{1 + x}} d x$ $\int \frac{1 - x}{\sqrt{1 - x^{2}}} d x$ $\int \frac{d x}{\sqrt{1 - x^{2}}} + \frac{1}{2} \int \frac{d (1 - x^{2})}{\sqrt{1 - x^{2}}}$ ${s i n}^{- 1} (x) + \frac{1}{2} \times \frac{{(1 - x^{2})}^{\frac{- 1}{2} + 1}}{\frac{1}{2}} + c$ $s o r e q u i r e d a n s w e r i s$ $∣ {s i n}^{- 1} x + {(1 - x^{2})}^{\frac{1}{2}} ∣_{0}^{1}$ $= {s i n}^{- 1} (1) + 0 - {s i n}^{- 1} (0) - {(1 - 0)}^{\frac{1}{2}}$ $= \frac{π}{2} - 1$
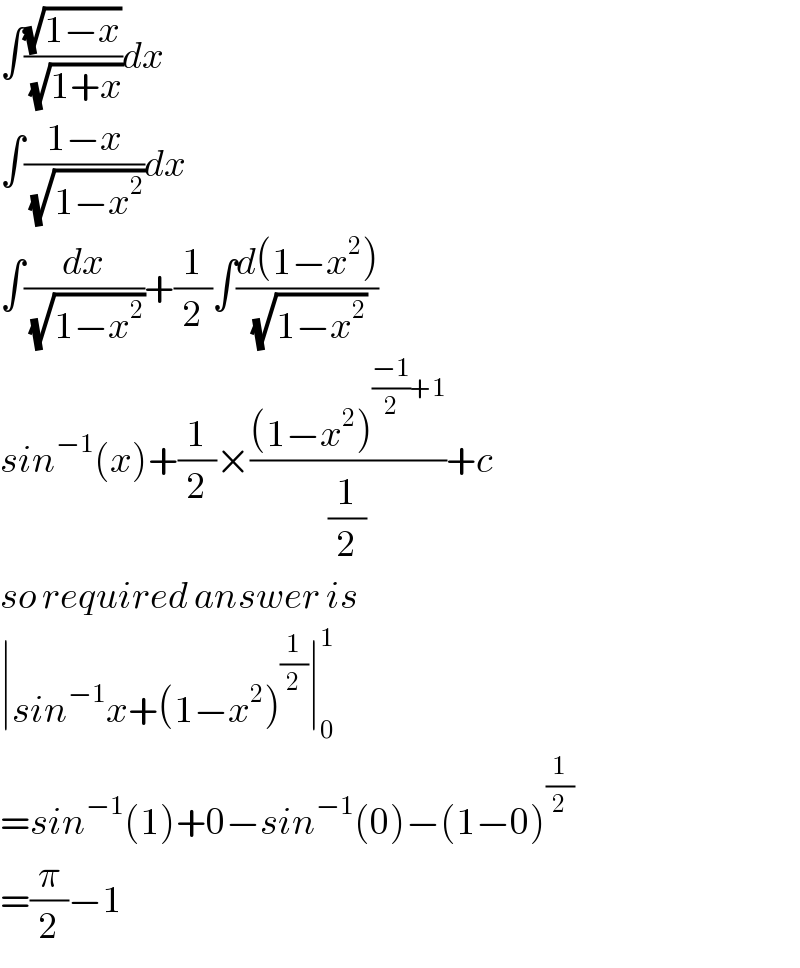
	Answered by ajfour last updated on 28/Jan/19

	$l e t x = \cos 2 θ$ $\int_{π / 4}^{0} \tan θ (- 4 \sin θ \cos θ) d θ$ $= 2 \int_{0}^{π / 4} (1 - \cos 2 θ) d θ$ $= \frac{π}{2} - 1 .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum