
Question and Answers Forum
Question Number 54194 by ajfour last updated on 30/Jan/19
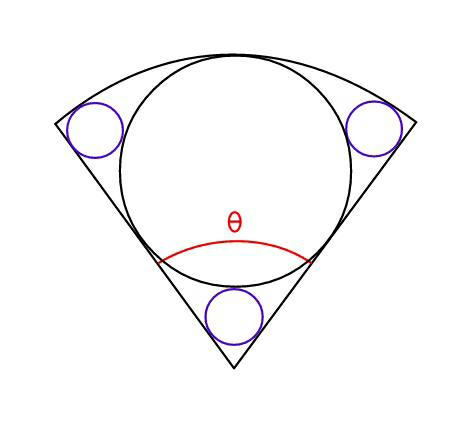
Commented by ajfour last updated on 31/Jan/19
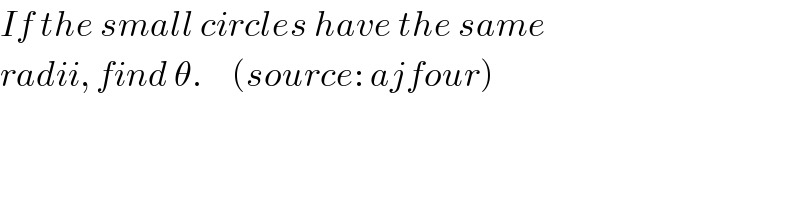
Answered by ajfour last updated on 30/Jan/19
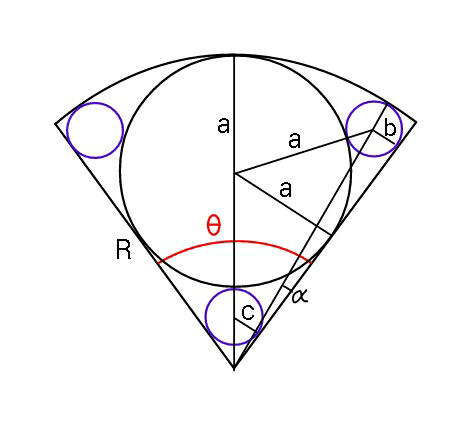
Commented by mr W last updated on 31/Jan/19
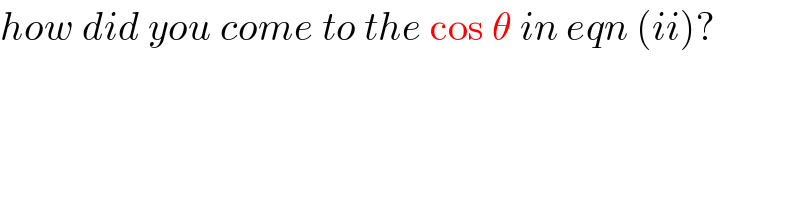
Commented by ajfour last updated on 31/Jan/19
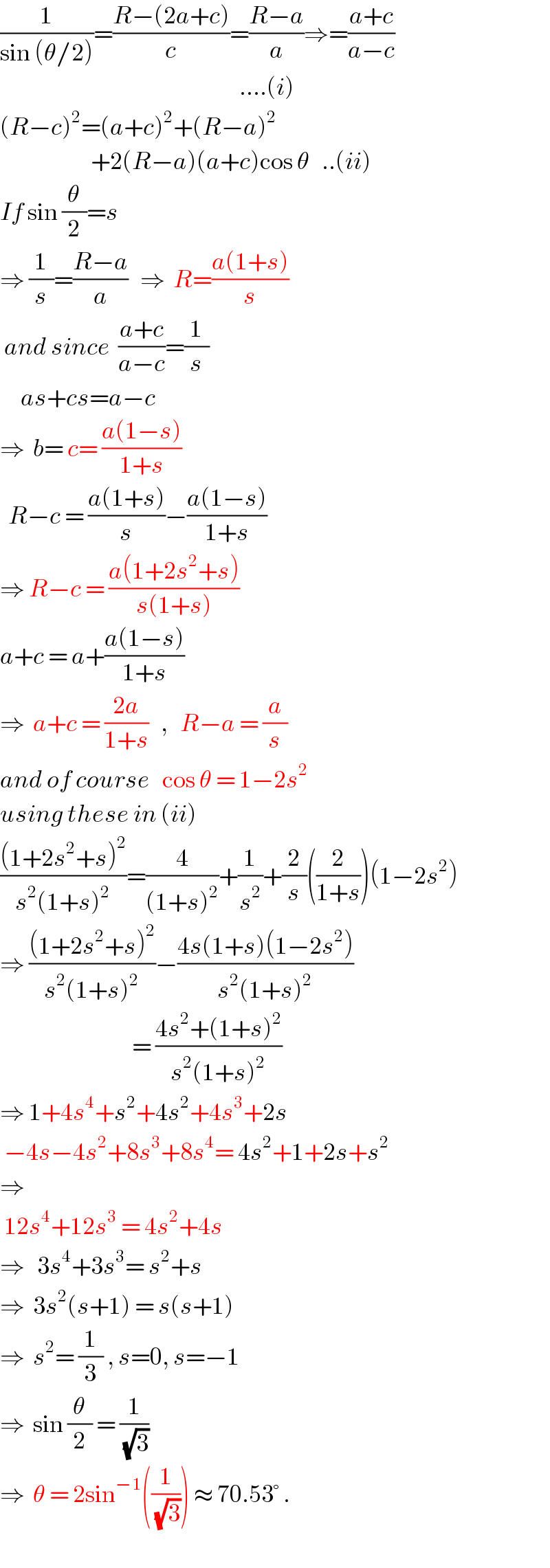
Commented by ajfour last updated on 31/Jan/19
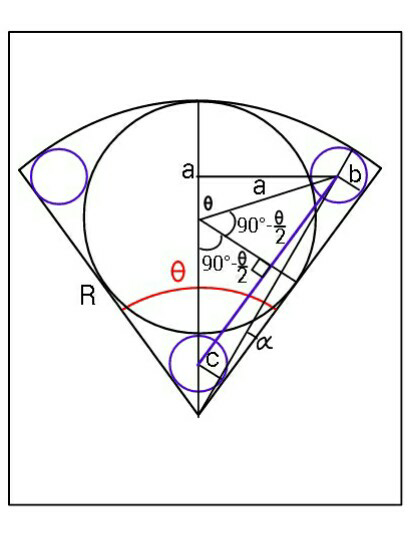
Commented by ajfour last updated on 31/Jan/19
![(R−b)^2 =(a+b)^2 sin^2 θ+ [(R−a)+(a+b)cos θ]^2 ⇒(R−b)^2 =(a+b)^2 +2(R−a)(a+b)cos θ and b=c ⇒(R−c)^2 =(a+c)^2 +2(R−a)(a+c)cos θ will that do Sir ?](Q54214.png)
Commented by mr W last updated on 31/Jan/19

