Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 54224 by rahul 19 last updated on 31/Jan/19

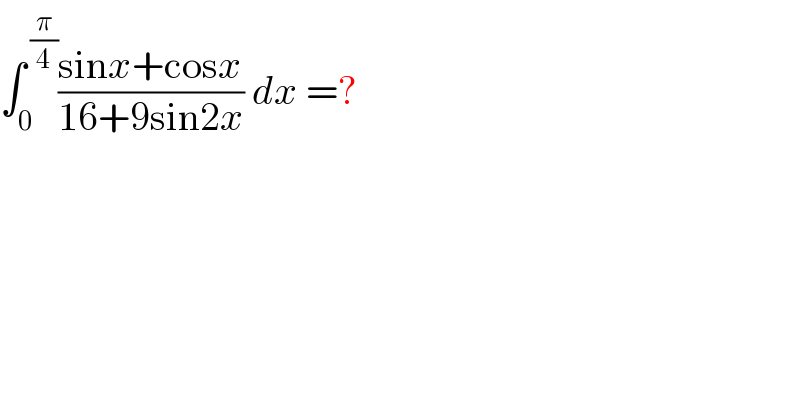
∫_0 ^( (π/4)) ((sinx+cosx)/(16+9sin2x)) dx =?

$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sin}{x}+\mathrm{cos}{x}}{\mathrm{16}+\mathrm{9sin2}{x}}\:{dx}\:=? \\ $$

Commented by Meritguide1234 last updated on 01/Feb/19

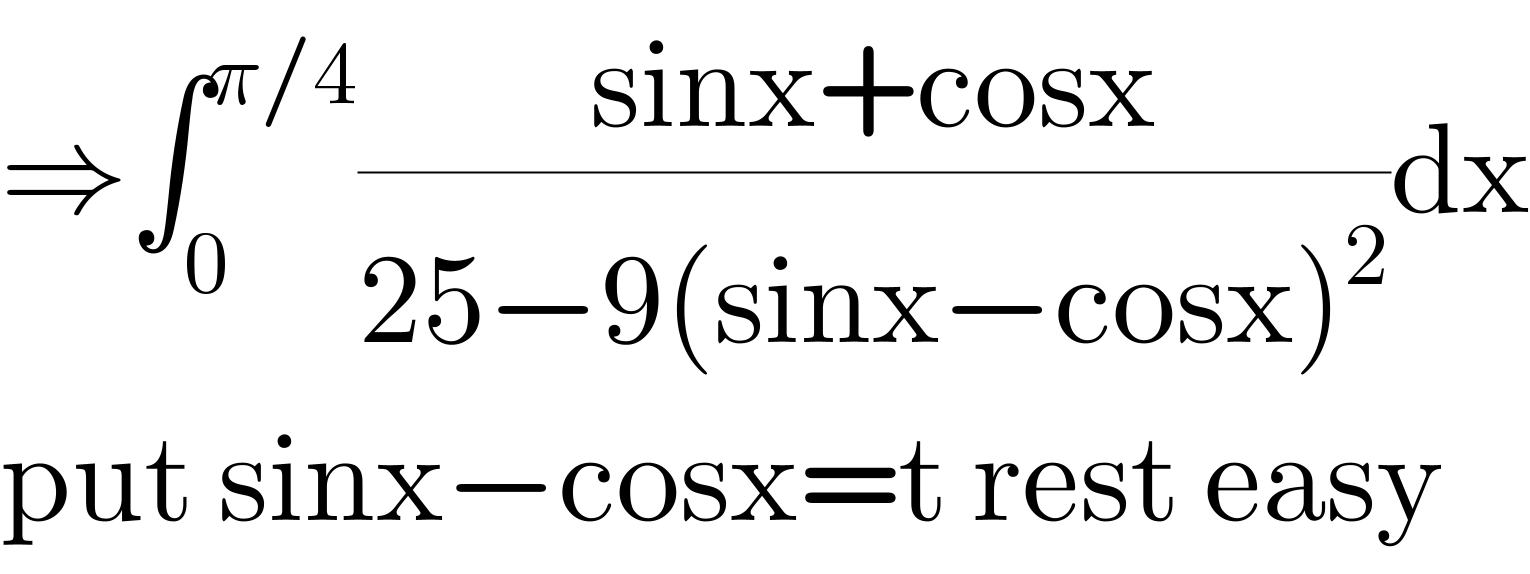
⇒∫_0 ^(π/4) ((sinx+cosx)/(25−9(sinx−cosx)^2 ))dx put sinx−cosx=t rest easy

$$\Rightarrow\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\mathrm{sinx}+\mathrm{cosx}}{\mathrm{25}−\mathrm{9}\left(\mathrm{sinx}−\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{put}\:\mathrm{sinx}−\mathrm{cosx}=\mathrm{t}\:\mathrm{rest}\:\mathrm{easy} \\ $$

Commented by rahul 19 last updated on 01/Feb/19

there is a little mistake in the denominator! �� Anyways, I've understood .

Commented by maxmathsup by imad last updated on 01/Feb/19

let I =∫_0 ^(π/4) ((sinx +cosx)/(16 +9sin(2x)))dx ⇒ I =∫_0 ^(π/4) ((sin(x+(π/4)))/(16 +9 sin(2x)))dx =_(x+(π/4)=t) ∫_(π/4) ^(π/2) ((sin(t))/(16 +9 sin(2t−(π/2))))dt =∫_(π/4) ^(π/2) ((sin(t))/(16 −9cos(2t)))dt =∫_(π/4) ^(π/2) ((sint dt)/(16−9(2cos^2 t−1))) =∫_(π/4) ^(π/2) ((sint dt)/(25−18 cos^2 t)) =_(cost=u) ∫_(1/(√2)) ^0 ((−du)/(25−18u^2 )) = −∫_0 ^(1/(√2)) (du/(18u^2 −25)) =−∫_0 ^(1/(√2)) (du/((3(√2)u)^2 −25)) =_(3(√2)u =5α) −∫_0 ^(3/5) (1/(25(u^2 −1))) ((5dα)/(3(√2))) =−(1/(15(√2))) ∫_0 ^(3/5) ((1/(u−1)) −(1/(u+1)))du =(1/(30(√2)))[ln∣((u+1)/(u−1))∣]_0 ^(3/5) =(1/(30(√2))) ln∣ (((3/5)+1)/((3/5)−1))∣ =(1/(30(√2))) ln((8/2)) =((2ln(2))/(30(√2))) =((ln(2))/(15(√2)))

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{sinx}\:+{cosx}}{\mathrm{16}\:+\mathrm{9}{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{16}\:+\mathrm{9}\:{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$=_{{x}+\frac{\pi}{\mathrm{4}}={t}} \:\:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left({t}\right)}{\mathrm{16}\:+\mathrm{9}\:{sin}\left(\mathrm{2}{t}−\frac{\pi}{\mathrm{2}}\right)}{dt}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left({t}\right)}{\mathrm{16}\:−\mathrm{9}{cos}\left(\mathrm{2}{t}\right)}{dt} \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sint}\:{dt}}{\mathrm{16}−\mathrm{9}\left(\mathrm{2}{cos}^{\mathrm{2}} {t}−\mathrm{1}\right)}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sint}\:{dt}}{\mathrm{25}−\mathrm{18}\:{cos}^{\mathrm{2}} {t}}\:=_{{cost}={u}} \:\:\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} ^{\mathrm{0}} \:\:\frac{−{du}}{\mathrm{25}−\mathrm{18}{u}^{\mathrm{2}} } \\ $$$$=\:−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \:\:\:\:\frac{{du}}{\mathrm{18}{u}^{\mathrm{2}} −\mathrm{25}}\:=−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \:\:\:\frac{{du}}{\left(\mathrm{3}\sqrt{\mathrm{2}}{u}\right)^{\mathrm{2}} −\mathrm{25}}\:=_{\mathrm{3}\sqrt{\mathrm{2}}{u}\:=\mathrm{5}\alpha} \:\:−\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{5}}} \:\frac{\mathrm{1}}{\mathrm{25}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}\:\frac{\mathrm{5}{d}\alpha}{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{15}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{5}}} \:\:\left(\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du}\:=\frac{\mathrm{1}}{\mathrm{30}\sqrt{\mathrm{2}}}\left[{ln}\mid\frac{{u}+\mathrm{1}}{{u}−\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{5}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{30}\sqrt{\mathrm{2}}}\:{ln}\mid\:\frac{\frac{\mathrm{3}}{\mathrm{5}}+\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{5}}−\mathrm{1}}\mid\:=\frac{\mathrm{1}}{\mathrm{30}\sqrt{\mathrm{2}}}\:{ln}\left(\frac{\mathrm{8}}{\mathrm{2}}\right)\:=\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{30}\sqrt{\mathrm{2}}}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{15}\sqrt{\mathrm{2}}} \\ $$

Commented by maxmathsup by imad last updated on 01/Feb/19

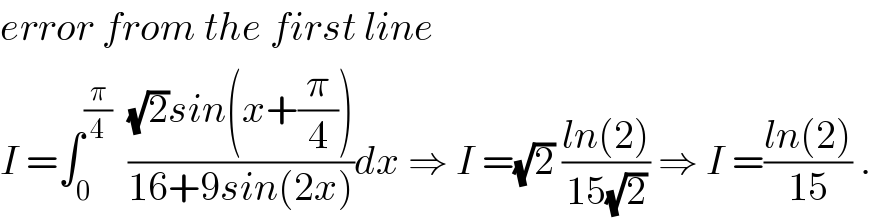
error from the first line I =∫_0 ^(π/4) (((√2)sin(x+(π/4)))/(16+9sin(2x)))dx ⇒ I =(√2) ((ln(2))/(15(√2))) ⇒ I =((ln(2))/(15)) .

$${error}\:{from}\:{the}\:{first}\:{line}\: \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\sqrt{\mathrm{2}}{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{16}+\mathrm{9}{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{I}\:=\sqrt{\mathrm{2}}\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{15}\sqrt{\mathrm{2}}}\:\Rightarrow\:{I}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{15}}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 31/Jan/19

∫_0 ^(π/4) ((d(sinx−cosx))/(16+9×2sinxcosx)) ∫_0 ^(π/4) ((d(sinx−cosx))/(25−9(1−2sinxcosx))) ∫_0 ^(π/4) ((d(sinx−cosx))/(25−9(sinx−cosx)^2 )) (1/9)∫_0 ^(π/4) ((d(sinx−cosx))/(((5/3))^2 −(sinx−cosx)^2 )) (1/9)×(1/(2((5/3))))∣ln((((5/3)+sinx−cosx)/((5/3)−sinx+cosx)))∣_0 ^(π/4) =(1/(30))[ln(1)−ln((((5/3)−1)/((5/3)+1)))] =−(1/(30))ln((1/4))=(1/(30))ln4=((ln2)/(15)) rahul pls check...pls upload answer of previous 8 inttegals you posred...

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{16}+\mathrm{9}×\mathrm{2}{sinxcosx}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{25}−\mathrm{9}\left(\mathrm{1}−\mathrm{2}{sinxcosx}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{25}−\mathrm{9}\left({sinx}−{cosx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} −\left({sinx}−{cosx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}×\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)}\mid{ln}\left(\frac{\frac{\mathrm{5}}{\mathrm{3}}+{sinx}−{cosx}}{\frac{\mathrm{5}}{\mathrm{3}}−{sinx}+{cosx}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{30}}\left[{ln}\left(\mathrm{1}\right)−{ln}\left(\frac{\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{1}}{\frac{\mathrm{5}}{\mathrm{3}}+\mathrm{1}}\right)\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{30}}{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{30}}{ln}\mathrm{4}=\frac{{ln}\mathrm{2}}{\mathrm{15}}\:{rahul}\:{pls}\:{check}...{pls}\:{upload}\:{answer}\:{of} \\ $$$${previous}\:\mathrm{8}\:{inttegals}\:{you}\:{posred}... \\ $$

Commented by rahul 19 last updated on 01/Feb/19

thank you sir!

Answered by Prithwish sen last updated on 31/Jan/19

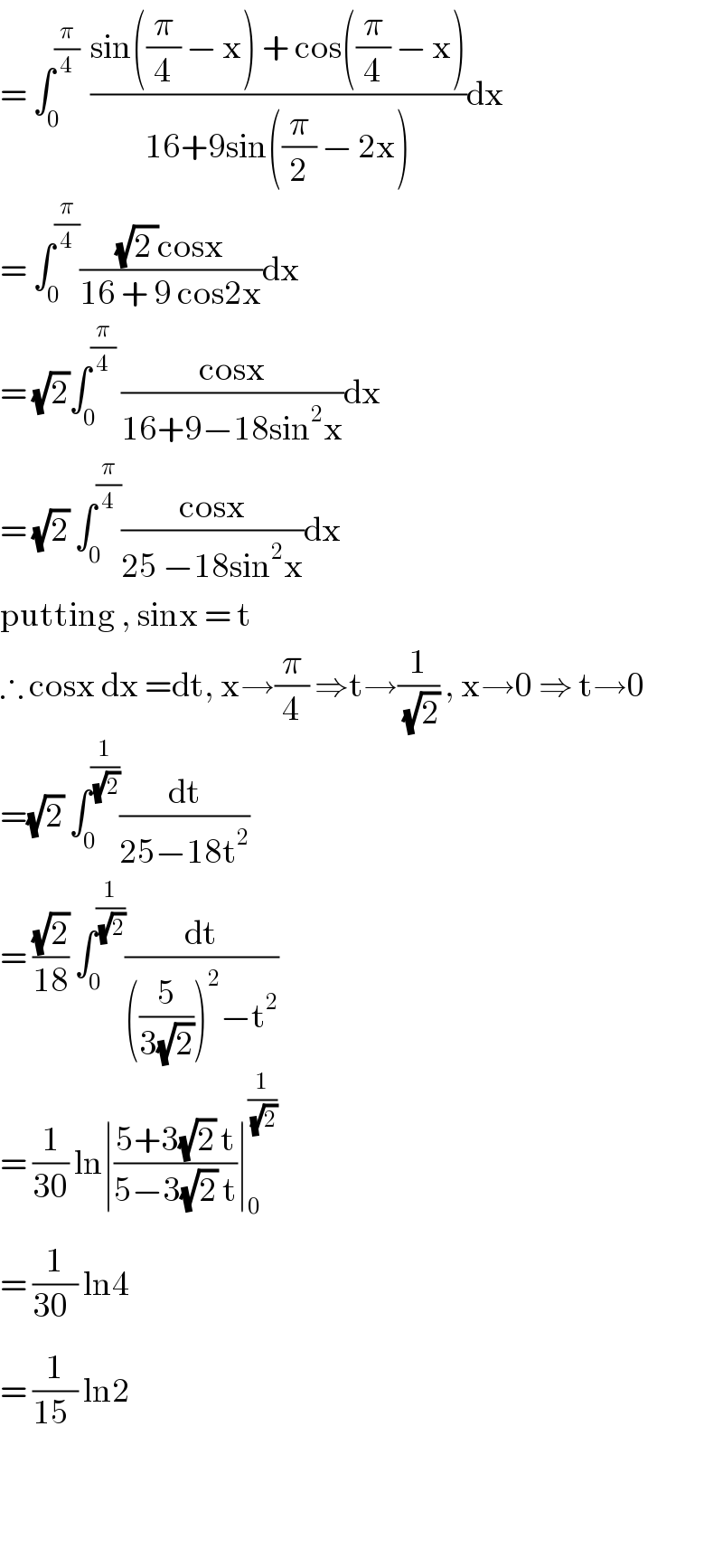
= ∫_0 ^(π/4) ((sin((π/4) − x) + cos((π/4) − x))/(16+9sin((π/2) − 2x)))dx = ∫_0 ^(π/4) (((√(2 ))cosx)/(16 + 9 cos2x))dx = (√2)∫_0 ^(π/4) ((cosx)/(16+9−18sin^2 x))dx = (√2) ∫_0 ^(π/4) ((cosx)/(25 −18sin^2 x))dx putting , sinx = t ∴ cosx dx =dt, x→(π/4) ⇒t→(1/(√2)) , x→0 ⇒ t→0 =(√2) ∫_0 ^(1/(√2)) (dt/(25−18t^2 )) = ((√2)/(18)) ∫_0 ^(1/(√2)) (dt/(((5/(3(√2))))^2 −t^2 )) = (1/(30)) ln∣((5+3(√2) t)/(5−3(√2) t))∣_0_ ^(1/(√2)) = (1/(30_ )) ln4 = (1/(15_ )) ln2

$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\:−\:\mathrm{x}\right)\:+\:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\:−\:\mathrm{x}\right)}{\mathrm{16}+\mathrm{9sin}\left(\frac{\pi}{\mathrm{2}}\:−\:\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\sqrt{\mathrm{2}\:}\mathrm{cosx}}{\mathrm{16}\:+\:\mathrm{9}\:\mathrm{cos2x}}\mathrm{dx} \\ $$$$=\:\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{cosx}}{\mathrm{16}+\mathrm{9}−\mathrm{18sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$=\:\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{cosx}}{\mathrm{25}\:−\mathrm{18sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{putting}\:,\:\mathrm{sinx}\:=\:\mathrm{t} \\ $$$$\therefore\:\mathrm{cosx}\:\mathrm{dx}\:=\mathrm{dt},\:\mathrm{x}\rightarrow\frac{\pi}{\mathrm{4}}\:\Rightarrow\mathrm{t}\rightarrow\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:,\:\mathrm{x}\rightarrow\mathrm{0}\:\Rightarrow\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \frac{\mathrm{dt}}{\mathrm{25}−\mathrm{18t}^{\mathrm{2}} } \\ $$$$=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{18}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \frac{\mathrm{dt}}{\left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{30}}\:\mathrm{ln}\mid\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}}\:\mathrm{t}}{\mathrm{5}−\mathrm{3}\sqrt{\mathrm{2}}\:\mathrm{t}}\mid_{\mathrm{0}_{} } ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{30}_{} }\:\mathrm{ln4} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{15}_{} }\:\mathrm{ln2} \\ $$$$ \\ $$$$\: \\ $$

Commented by rahul 19 last updated on 01/Feb/19

thank you sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com