Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 5427 by Rasheed Soomro last updated on 14/May/16

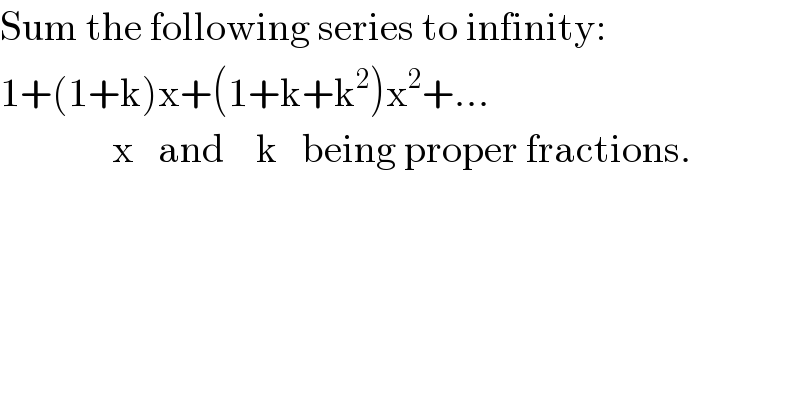
Sum the following series to infinity: 1+(1+k)x+(1+k+k^2 )x^2 +... x and k being proper fractions.

$$\mathrm{Sum}\:\mathrm{the}\:\mathrm{following}\:\mathrm{series}\:\mathrm{to}\:\mathrm{infinity}: \\ $$$$\mathrm{1}+\left(\mathrm{1}+\mathrm{k}\right)\mathrm{x}+\left(\mathrm{1}+\mathrm{k}+\mathrm{k}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} +... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\:\:\mathrm{and}\:\:\:\:\mathrm{k}\:\:\:\mathrm{being}\:\mathrm{proper}\:\mathrm{fractions}. \\ $$

Commented by Yozzii last updated on 14/May/16

Let s=1+(1+k)x+(1+k+k^2 )x^2 +... Since k^(r+1) −1=(k−1)(1+k+k^2 +k^3 +...+k^r ) ⇒1−k^(r+1) =(1−k)(1+k+k^2 +...+k^r ) ⇒((1−k^(r+1) )/(1−k))=Σ_(j=0) ^r k^j (k∈F⇒k≠1) ∴ r=0⇒((1−k)/(1−k))=1 r=1⇒((1−k^2 )/(1−k))=1+k and so on. ∴ s=lim_(n→∞) (Σ_(r=0) ^n ((1−k^(r+1) )/(1−k))x^r ) (k∈F⇒k≠1) s=(1/(1−k))lim_(n→∞) (Σ_(r=0) ^n x^r −k(kx)^r ) Since x and k are proper fractions ⇒{x^r }_(r=0) ^∞ and {(kx)^r }_(r=0) ^∞ are infinite,convergent geometric progressions ⇒lim_(n→∞) Σ_(r=0) ^n x^r =(1/(1−x)) and lim_(n→∞) Σ_(r=0) ^n (kx)^r =(1/(1−kx)) ⇒s=(1/(1−k))((1/(1−x))−(k/(1−kx))) s=((1−kx−k+kx)/((1−k)(1−x)(1−kx))) s=(1/((1−x)(1−kx))) 1+(k+1)x+(1+k+k^2 )x^2 +...=(1/((1−x)(1−kx))) (k≠1, x≠(1/k))

$${Let}\:{s}=\mathrm{1}+\left(\mathrm{1}+{k}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +... \\ $$$${Since}\:{k}^{{r}+\mathrm{1}} −\mathrm{1}=\left({k}−\mathrm{1}\right)\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +{k}^{\mathrm{3}} +...+{k}^{{r}} \right) \\ $$$$\Rightarrow\mathrm{1}−{k}^{{r}+\mathrm{1}} =\left(\mathrm{1}−{k}\right)\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +...+{k}^{{r}} \right) \\ $$$$\Rightarrow\frac{\mathrm{1}−{k}^{{r}+\mathrm{1}} }{\mathrm{1}−{k}}=\underset{{j}=\mathrm{0}} {\overset{{r}} {\sum}}{k}^{{j}} \:\:\:\left({k}\in\mathbb{F}\Rightarrow{k}\neq\mathrm{1}\right) \\ $$$$\therefore\:{r}=\mathrm{0}\Rightarrow\frac{\mathrm{1}−{k}}{\mathrm{1}−{k}}=\mathrm{1} \\ $$$${r}=\mathrm{1}\Rightarrow\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\mathrm{1}+{k} \\ $$$${and}\:{so}\:{on}. \\ $$$$\therefore\:{s}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}−{k}^{{r}+\mathrm{1}} }{\mathrm{1}−{k}}{x}^{{r}} \right)\:\left({k}\in\mathbb{F}\Rightarrow{k}\neq\mathrm{1}\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{1}−{k}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{r}} −{k}\left({kx}\right)^{{r}} \right) \\ $$$${Since}\:{x}\:{and}\:{k}\:{are}\:{proper}\:{fractions} \\ $$$$\Rightarrow\left\{{x}^{{r}} \right\}_{{r}=\mathrm{0}} ^{\infty} \:{and}\:\left\{\left({kx}\right)^{{r}} \right\}_{{r}=\mathrm{0}} ^{\infty} \:\:{are}\:{infinite},{convergent}\:{geometric}\: \\ $$$${progressions} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{and}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\left({kx}\right)^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{kx}} \\ $$$$\Rightarrow{s}=\frac{\mathrm{1}}{\mathrm{1}−{k}}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}−\frac{{k}}{\mathrm{1}−{kx}}\right) \\ $$$${s}=\frac{\mathrm{1}−{kx}−{k}+{kx}}{\left(\mathrm{1}−{k}\right)\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)} \\ $$$${s}=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)} \\ $$$$\mathrm{1}+\left({k}+\mathrm{1}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +...=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)}\:\:\left({k}\neq\mathrm{1},\:{x}\neq\frac{\mathrm{1}}{{k}}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 14/May/16

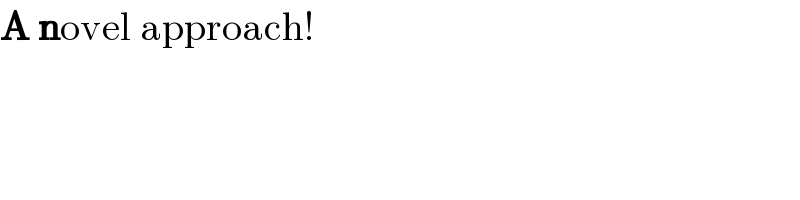
A novel approach!

$$\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{n}}\mathrm{ovel}\:\mathrm{approach}! \\ $$

Answered by nchejane last updated on 14/May/16

1+(1+k)x+(1+k+k^2 )x^2 +(1+k+k^2 +k^3 )x^3 +... =(1+x+x^2 +x^3 +...)+k(x+x^2 +x^3 +...)+k^2 (x^2 +x^3 +x^4 +...)+... =(1/(1−x))+k(x/(1−x))+k^2 (x^2 /(1−x))+k^3 (x^3 /(1−x))+...(since abs(x)<1 ) =(1/(1−x))[1+kx+(kx)^2 +(kx)^3 +...] =(1/(1−x))×(1/(1−kx)) (since abs(kx)<1)

$$\mathrm{1}+\left(\mathrm{1}+{k}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +{k}^{\mathrm{3}} \right){x}^{\mathrm{3}} +... \\ $$$$=\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)+{k}\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)+{k}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +...\right)+... \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}+{k}\frac{{x}}{\mathrm{1}−{x}}+{k}^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}}+{k}^{\mathrm{3}} \frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}}+...\left({since}\:{abs}\left({x}\right)<\mathrm{1}\:\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}\left[\mathrm{1}+{kx}+\left({kx}\right)^{\mathrm{2}} +\left({kx}\right)^{\mathrm{3}} +...\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}×\frac{\mathrm{1}}{\mathrm{1}−{kx}}\:\:\left({since}\:{abs}\left({kx}\right)<\mathrm{1}\right) \\ $$

Commented by Rasheed Soomro last updated on 14/May/16

Nice approach!

$$\boldsymbol{\mathrm{N}}\mathrm{ice}\:\boldsymbol{\mathrm{a}}\mathrm{pproach}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com