
Question and Answers Forum
Question Number 54273 by rahul 19 last updated on 01/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Feb/19
![(df/dx)=f(x)+∫_0 ^1 f(x)dx (df/dx)=f(x)+a (df/(f(x)+a))=dx ((d[f(x)+a])/(f(x)+a))=dx ln[f(x)+a]=x+c f(x)+a=e^(x+c) f(0)+a=e^(0+c) 1+a=e^c f(x)+a=e^x ×e^c f(x)+a=e^x (1+a) f(x)+a=e^x +ae^x f(x)=(1+a)e^x −a ∫_0 ^1 f(x)dx=(1+a)∫_0 ^1 e^x dx−a∫_0 ^1 dx a=(1+a)(e−1)−a 2a=e−1+ae−a 3a−ae=e−1 a=((e−1)/(3−e)) f(x)=(1+a)e^x −a =(1+((e−1)/(3−e)))e^x −((e−1)/(3−e)) f(x)=(2/(3−e))e^x −((e−1)/(3−e)) ∫f(x)dx=(2/(3−e))e^x +((1−e)/(3−e))x+c so option b is answer](Q54277.png)
Commented by rahul 19 last updated on 01/Feb/19
thank you sir!
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Feb/19

Commented by tanmay.chaudhury50@gmail.com last updated on 01/Feb/19

Commented by tanmay.chaudhury50@gmail.com last updated on 02/Feb/19

Commented by rahul 19 last updated on 02/Feb/19
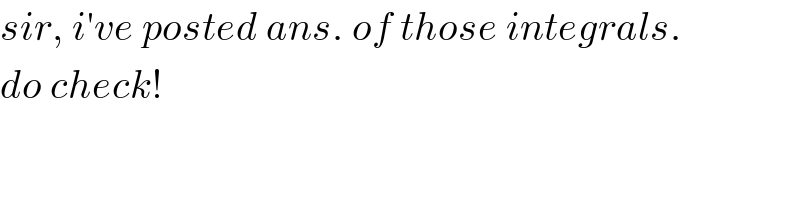
Commented by rahul 19 last updated on 03/Feb/19

Answered by ajfour last updated on 01/Feb/19
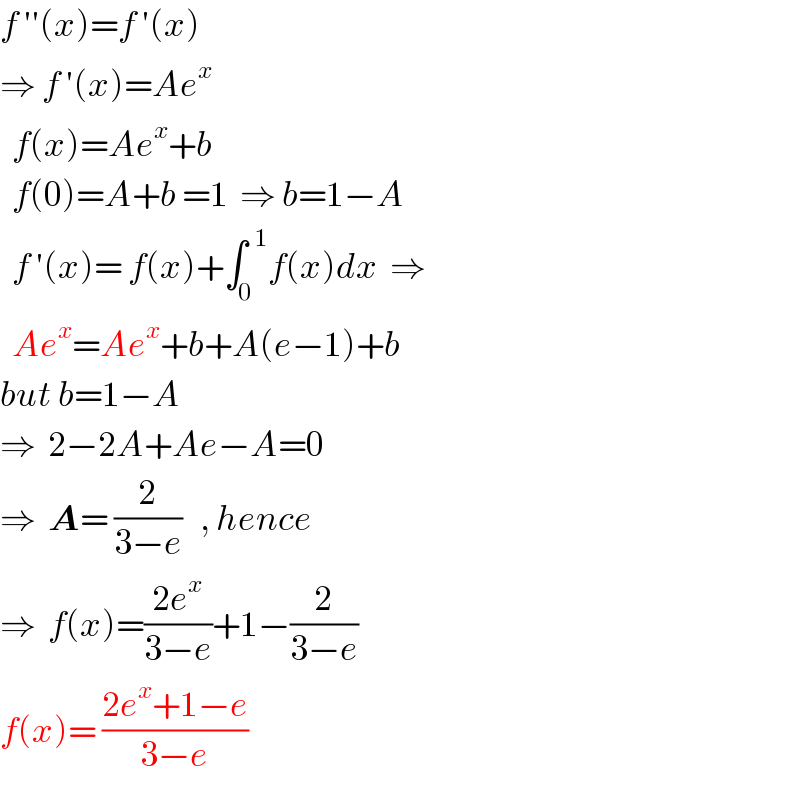
Commented by ajfour last updated on 02/Feb/19

Commented by rahul 19 last updated on 02/Feb/19
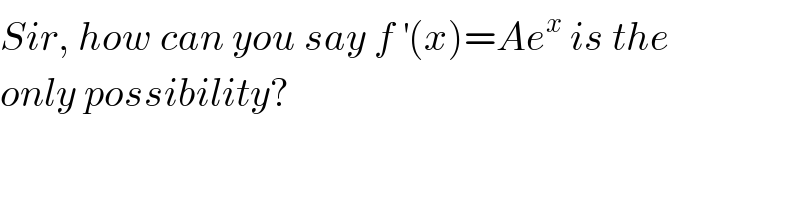
Commented by ajfour last updated on 02/Feb/19
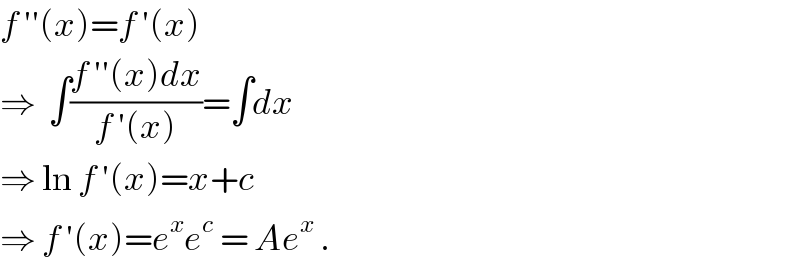
Commented by rahul 19 last updated on 03/Feb/19

