Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 54372 by maxmathsup by imad last updated on 02/Feb/19

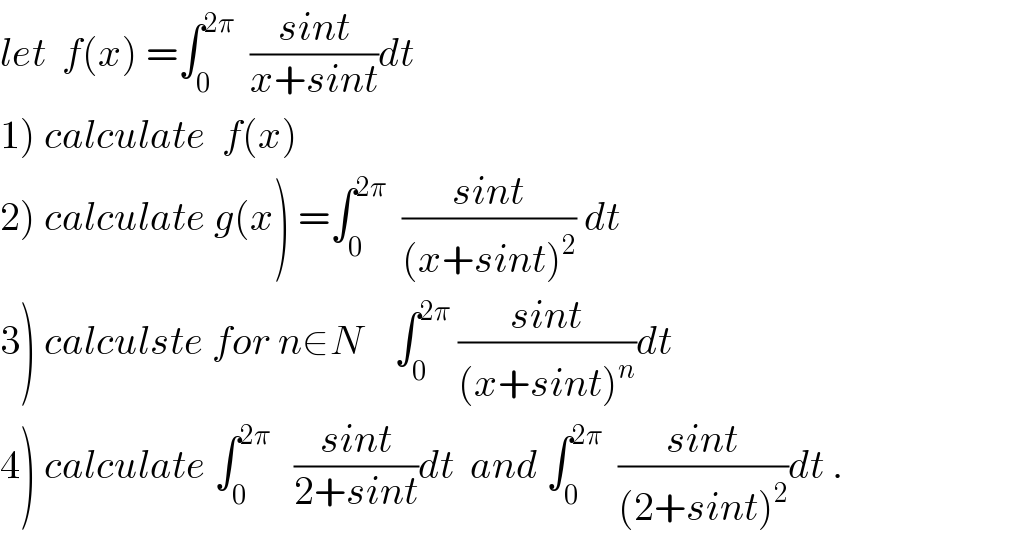
let f(x) =∫_0 ^(2π) ((sint)/(x+sint))dt 1) calculate f(x) 2) calculate g(x) =∫_0 ^(2π) ((sint)/((x+sint)^2 )) dt 3) calculste for n∈N ∫_0 ^(2π) ((sint)/((x+sint)^n ))dt 4) calculate ∫_0 ^(2π) ((sint)/(2+sint))dt and ∫_0 ^(2π) ((sint)/((2+sint)^2 ))dt .

$${let}\:\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{{x}+{sint}}{dt}\:\:\: \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{\left({x}+{sint}\right)^{\mathrm{2}} }\:{dt}\: \\ $$$$\left.\mathrm{3}\right)\:{calculste}\:{for}\:{n}\in{N}\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{sint}}{\left({x}+{sint}\right)^{{n}} }{dt}\: \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{sint}}{\mathrm{2}+{sint}}{dt}\:\:{and}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{\left(\mathrm{2}+{sint}\right)^{\mathrm{2}} }{dt}\:. \\ $$

Commented by maxmathsup by imad last updated on 03/Feb/19

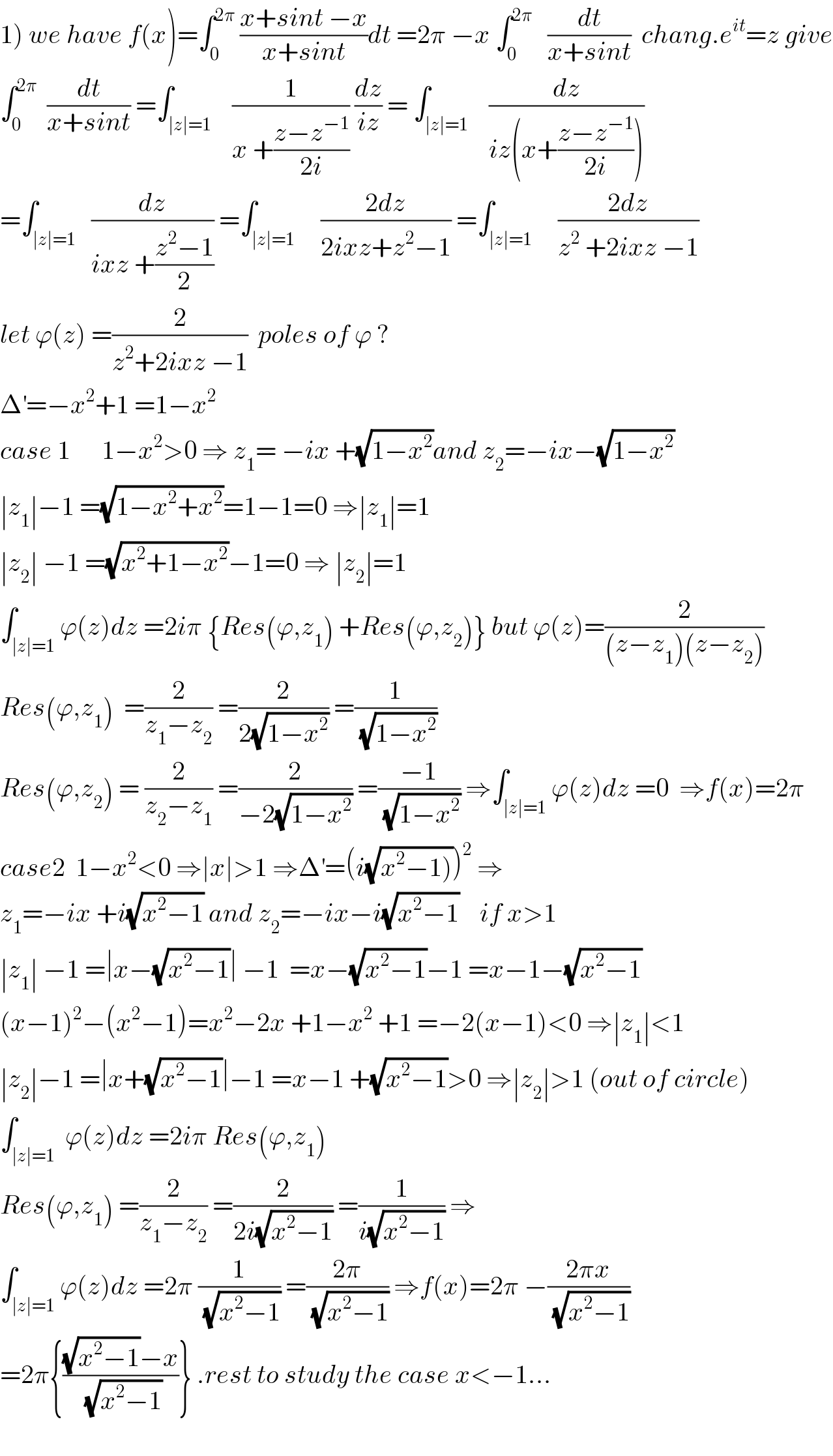
1) we have f(x)=∫_0 ^(2π) ((x+sint −x)/(x+sint))dt =2π −x ∫_0 ^(2π) (dt/(x+sint)) chang.e^(it) =z give ∫_0 ^(2π) (dt/(x+sint)) =∫_(∣z∣=1) (1/(x +((z−z^(−1) )/(2i)))) (dz/(iz)) = ∫_(∣z∣=1) (dz/(iz(x+((z−z^(−1) )/(2i))))) =∫_(∣z∣=1) (dz/(ixz +((z^2 −1)/2))) =∫_(∣z∣=1) ((2dz)/(2ixz+z^2 −1)) =∫_(∣z∣=1) ((2dz)/(z^2 +2ixz −1)) let ϕ(z) =(2/(z^2 +2ixz −1)) poles of ϕ ? Δ^′ =−x^2 +1 =1−x^2 case 1 1−x^2 >0 ⇒ z_1 = −ix +(√(1−x^2 ))and z_2 =−ix−(√(1−x^2 )) ∣z_1 ∣−1 =(√(1−x^2 +x^2 ))=1−1=0 ⇒∣z_1 ∣=1 ∣z_2 ∣ −1 =(√(x^2 +1−x^2 ))−1=0 ⇒ ∣z_2 ∣=1 ∫_(∣z∣=1) ϕ(z)dz =2iπ {Res(ϕ,z_1 ) +Res(ϕ,z_2 )} but ϕ(z)=(2/((z−z_1 )(z−z_2 ))) Res(ϕ,z_1 ) =(2/(z_1 −z_2 )) =(2/(2(√(1−x^2 )))) =(1/(√(1−x^2 ))) Res(ϕ,z_2 ) = (2/(z_2 −z_1 )) =(2/(−2(√(1−x^2 )))) =((−1)/(√(1−x^2 ))) ⇒∫_(∣z∣=1) ϕ(z)dz =0 ⇒f(x)=2π case2 1−x^2 <0 ⇒∣x∣>1 ⇒Δ^′ =(i(√(x^2 −1))))^2 ⇒ z_1 =−ix +i(√(x^2 −1)) and z_2 =−ix−i(√(x^2 −1)) if x>1 ∣z_1 ∣ −1 =∣x−(√(x^2 −1))∣ −1 =x−(√(x^2 −1))−1 =x−1−(√(x^2 −1)) (x−1)^2 −(x^2 −1)=x^2 −2x +1−x^2 +1 =−2(x−1)<0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1 =∣x+(√(x^2 −1))∣−1 =x−1 +(√(x^2 −1))>0 ⇒∣z_2 ∣>1 (out of circle) ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) Res(ϕ,z_1 ) =(2/(z_1 −z_2 )) =(2/(2i(√(x^2 −1)))) =(1/(i(√(x^2 −1)))) ⇒ ∫_(∣z∣=1) ϕ(z)dz =2π (1/(√(x^2 −1))) =((2π)/(√(x^2 −1))) ⇒f(x)=2π −((2πx)/(√(x^2 −1))) =2π{(((√(x^2 −1))−x)/(√(x^2 −1)))} .rest to study the case x<−1...

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{x}+{sint}\:−{x}}{{x}+{sint}}{dt}\:=\mathrm{2}\pi\:−{x}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{x}+{sint}}\:\:{chang}.{e}^{{it}} ={z}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{{x}+{sint}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{x}\:+\frac{{z}−{z}^{−\mathrm{1}} }{\mathrm{2}{i}}}\:\frac{{dz}}{{iz}}\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{{dz}}{{iz}\left({x}+\frac{{z}−{z}^{−\mathrm{1}} }{\mathrm{2}{i}}\right)} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{{dz}}{{ixz}\:+\frac{{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{dz}}{\mathrm{2}{ixz}+{z}^{\mathrm{2}} −\mathrm{1}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{dz}}{{z}^{\mathrm{2}} \:+\mathrm{2}{ixz}\:−\mathrm{1}} \\ $$$${let}\:\varphi\left({z}\right)\:=\frac{\mathrm{2}}{{z}^{\mathrm{2}} +\mathrm{2}{ixz}\:−\mathrm{1}}\:\:{poles}\:{of}\:\varphi\:? \\ $$$$\Delta^{'} =−{x}^{\mathrm{2}} +\mathrm{1}\:=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${case}\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}−{x}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\:{z}_{\mathrm{1}} =\:−{ix}\:+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{and}\:{z}_{\mathrm{2}} =−{ix}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\mathrm{1}−\mathrm{1}=\mathrm{0}\:\Rightarrow\mid{z}_{\mathrm{1}} \mid=\mathrm{1} \\ $$$$\mid{z}_{\mathrm{2}} \mid\:−\mathrm{1}\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{2}} \mid=\mathrm{1} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{{Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:+{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\right\}\:{but}\:\varphi\left({z}\right)=\frac{\mathrm{2}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:\:=\frac{\mathrm{2}}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:=\:\frac{\mathrm{2}}{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\:=\frac{\mathrm{2}}{−\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\frac{−\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{0}\:\:\Rightarrow{f}\left({x}\right)=\mathrm{2}\pi \\ $$$${case}\mathrm{2}\:\:\mathrm{1}−{x}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\mid{x}\mid>\mathrm{1}\:\Rightarrow\Delta^{'} =\left({i}\sqrt{\left.{x}^{\mathrm{2}} −\mathrm{1}\right)}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${z}_{\mathrm{1}} =−{ix}\:+{i}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:{and}\:{z}_{\mathrm{2}} =−{ix}−{i}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\:\:\:{if}\:{x}>\mathrm{1} \\ $$$$\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\mid{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\mid\:−\mathrm{1}\:\:={x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\:={x}−\mathrm{1}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}−{x}^{\mathrm{2}} \:+\mathrm{1}\:=−\mathrm{2}\left({x}−\mathrm{1}\right)<\mathrm{0}\:\Rightarrow\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mid{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\mid−\mathrm{1}\:={x}−\mathrm{1}\:+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}>\mathrm{0}\:\Rightarrow\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:\left({out}\:{of}\:{circle}\right) \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\frac{\mathrm{2}}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{2}{i}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{\mathrm{1}}{{i}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}\pi\:\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{\mathrm{2}\pi}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow{f}\left({x}\right)=\mathrm{2}\pi\:−\frac{\mathrm{2}\pi{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\mathrm{2}\pi\left\{\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\right\}\:.{rest}\:{to}\:{study}\:{the}\:{case}\:{x}<−\mathrm{1}... \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 03/Feb/19

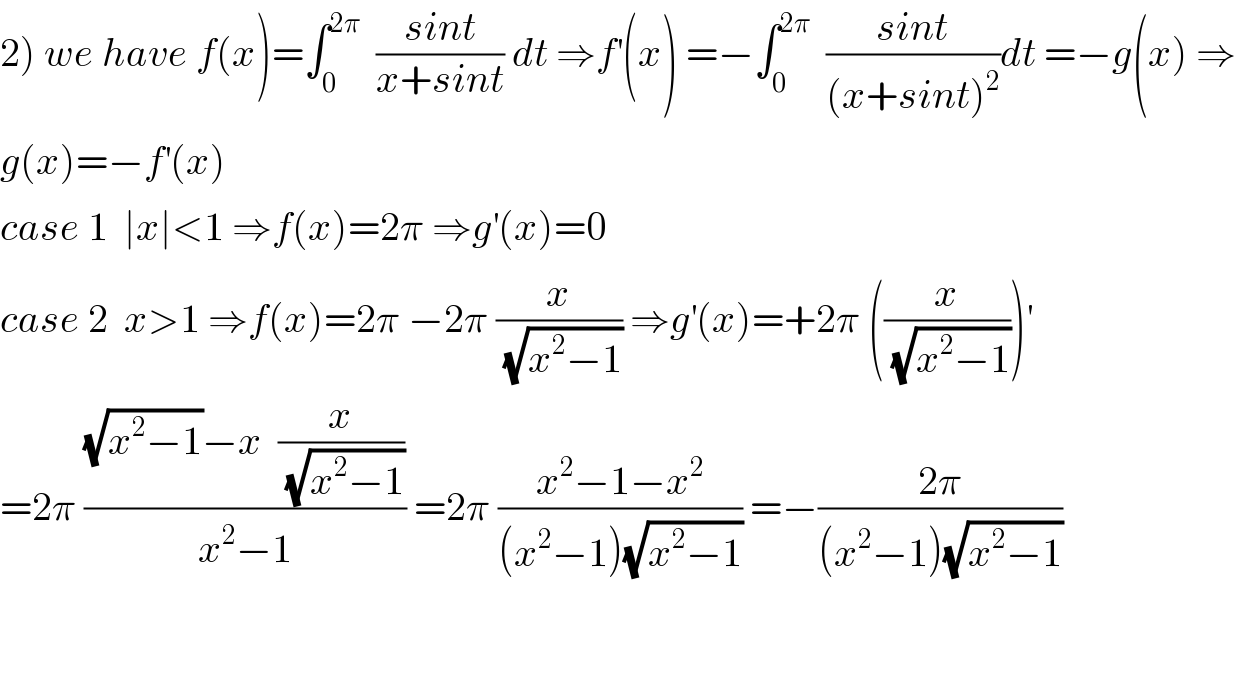
2) we have f(x)=∫_0 ^(2π) ((sint)/(x+sint)) dt ⇒f^′ (x) =−∫_0 ^(2π) ((sint)/((x+sint)^2 ))dt =−g(x) ⇒ g(x)=−f^′ (x) case 1 ∣x∣<1 ⇒f(x)=2π ⇒g^′ (x)=0 case 2 x>1 ⇒f(x)=2π −2π (x/(√(x^2 −1))) ⇒g^′ (x)=+2π ((x/(√(x^2 −1))))^′ =2π (((√(x^2 −1))−x (x/(√(x^2 −1))))/(x^2 −1)) =2π ((x^2 −1−x^2 )/((x^2 −1)(√(x^2 −1)))) =−((2π)/((x^2 −1)(√(x^2 −1))))

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{{x}+{sint}}\:{dt}\:\Rightarrow{f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{\left({x}+{sint}\right)^{\mathrm{2}} }{dt}\:=−{g}\left({x}\right)\:\Rightarrow \\ $$$${g}\left({x}\right)=−{f}^{'} \left({x}\right) \\ $$$${case}\:\mathrm{1}\:\:\mid{x}\mid<\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\mathrm{2}\pi\:\Rightarrow{g}^{'} \left({x}\right)=\mathrm{0} \\ $$$${case}\:\mathrm{2}\:\:{x}>\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\mathrm{2}\pi\:−\mathrm{2}\pi\:\frac{{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow{g}^{'} \left({x}\right)=+\mathrm{2}\pi\:\left(\frac{{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\right)^{'} \\ $$$$=\mathrm{2}\pi\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−{x}\:\:\frac{{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}\pi\:\frac{{x}^{\mathrm{2}} −\mathrm{1}−{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=−\frac{\mathrm{2}\pi}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$ \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 03/Feb/19

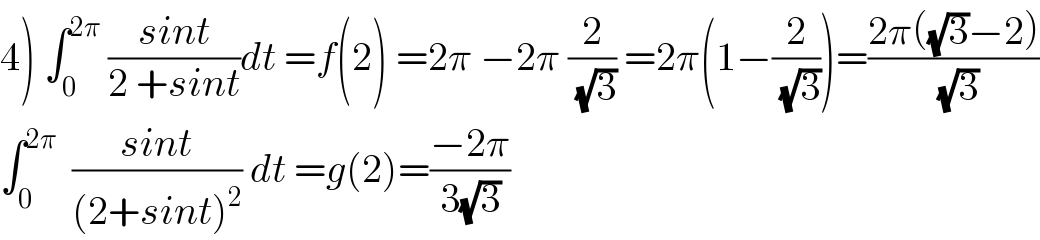
4) ∫_0 ^(2π) ((sint)/(2 +sint))dt =f(2) =2π −2π (2/(√3)) =2π(1−(2/(√3)))=((2π((√3)−2))/(√3)) ∫_0 ^(2π) ((sint)/((2+sint)^2 )) dt =g(2)=((−2π)/(3(√3)))

$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{sint}}{\mathrm{2}\:+{sint}}{dt}\:={f}\left(\mathrm{2}\right)\:=\mathrm{2}\pi\:−\mathrm{2}\pi\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:=\mathrm{2}\pi\left(\mathrm{1}−\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{2}\pi\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)}{\sqrt{\mathrm{3}}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sint}}{\left(\mathrm{2}+{sint}\right)^{\mathrm{2}} }\:{dt}\:={g}\left(\mathrm{2}\right)=\frac{−\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

1)∫_0 ^(2π) ((sint)/(x+sint))dt ∫((x+sint−x)/(x+sint))dt ∫dt−x∫(dt/(x+((2tan(t/2))/(1+tan^2 (t/2))))) ∫dt−x∫((sec^2 (t/2))/(xtan^2 (t/2)+x+2tan(t/2)))dt ∫dt−∫((sec^2 (t/2))/(tan^2 (t/2)+2tan(t/2)×(1/x)+(1/x^2 )+1−(1/x^2 ))) ∫dt−2∫((sec^2 (t/2)×(1/2))/((tan(t/2)+(1/x))^2 +((√(1−(1/x^2 ))) )^2 )) ∫dt−2∫((d(tan(t/2)+(1/x)))/((tan(t/2)+(1/x))^2 +((√(1−(1/x^2 ))) )^2 )) so answer is ∣t−(2/(√(1−(1/x^2 ))))tan^(−1) (((tan(t/2)+(1/x))/((√(1−(1/x^2 ))) )))∣_0 ^(2π) =[2π−{(2/(√(1−(1/x^2 ))))tan^(−1) (((tanπ+(1/x))/(√(1−(1/x^2 ))))−((tan0+(1/x))/(√(1−(1/x^2 )))))] =2π pls check mistKe if any...

$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{sint}}{{x}+{sint}}{dt} \\ $$$$\int\frac{{x}+{sint}−{x}}{{x}+{sint}}{dt} \\ $$$$\int{dt}−{x}\int\frac{{dt}}{{x}+\frac{\mathrm{2}{tan}\frac{{t}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}}} \\ $$$$\int{dt}−{x}\int\frac{{sec}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}}{{xtan}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}+{x}+\mathrm{2}{tan}\frac{{t}}{\mathrm{2}}}{dt} \\ $$$$\int{dt}−\int\frac{{sec}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}}{{tan}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}+\mathrm{2}{tan}\frac{{t}}{\mathrm{2}}×\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\int{dt}−\mathrm{2}\int\frac{{sec}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}}{\left({tan}\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:\right)^{\mathrm{2}} }\: \\ $$$$\int{dt}−\mathrm{2}\int\frac{{d}\left({tan}\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{{x}}\right)}{\left({tan}\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:\right)^{\mathrm{2}} } \\ $$$${so}\:{answer}\:{is} \\ $$$$\mid{t}−\frac{\mathrm{2}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:}\right)\mid_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=\left[\mathrm{2}\pi−\left\{\frac{\mathrm{2}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\pi+\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}−\frac{{tan}\mathrm{0}+\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\right)\right]\right. \\ $$$$=\mathrm{2}\pi \\ $$$${pls}\:{check}\:{mistKe}\:{if}\:{any}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com