
Question and Answers Forum
Question Number 54374 by maxmathsup by imad last updated on 02/Feb/19
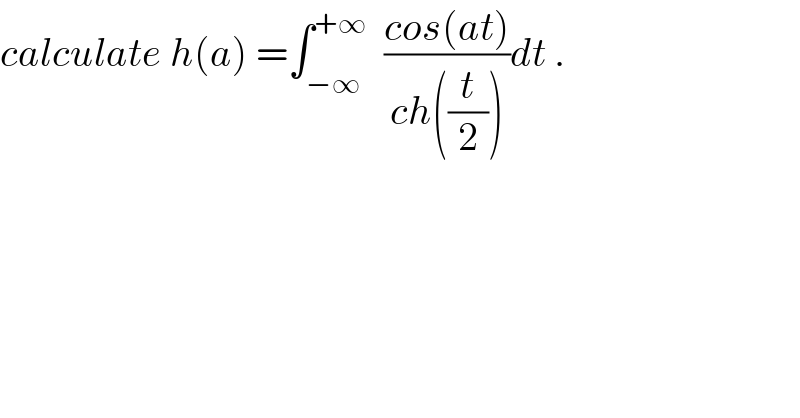
Commented by Abdo msup. last updated on 08/Feb/19
![h(a)=_((t/2)=x) 2 ∫_(−∞) ^(+∞) ((cos(2ax))/(ch(x)))dx =4 ∫_0 ^∞ ((cos(2ax))/((e^x +e^(−x) )/2))dx =8 ∫_0 ^∞ ((e^(−x) cos(2ax))/(1+e^(−2x) ))dx =8 ∫_0 ^∞ e^(−x) cos(2ax)(Σ_(n=0) ^∞ (−1)^n e^(−2nx) )dx =8 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)x) cos(2ax)dx let A_n =∫_0 ^∞ e^(−(2n+1)x) cos(2ax)dx ⇒ A_n =Re( ∫_0 ^∞ e^(−(2n+1)x) e^(2iax) dx) but ∫_0 ^∞ e^((−(2n+1)+2ia)x) dx=[(1/(−(2n+1)+2ia)) e^((−(2n+1)+2ia)x) ]_0 ^(+∞) = (1/(−(2n+1)+2ia)) =−(1/((2n+1)−2ia)) =−((2n+1 +2ia)/((2n+1)^2 +4a^2 )) ⇒ A_n =−((2n+1)/((2n+1)^2 +4a^2 )) ⇒ h(a)=8 Σ_(n=0) ^∞ (−1)^(n+1) ((2n+1)/((2n+1)^2 +4a^2 )) and this serie can be calculated by fourier series ...be continued...](Q54638.png)
| ||
Question and Answers Forum | ||
Question Number 54374 by maxmathsup by imad last updated on 02/Feb/19 | ||
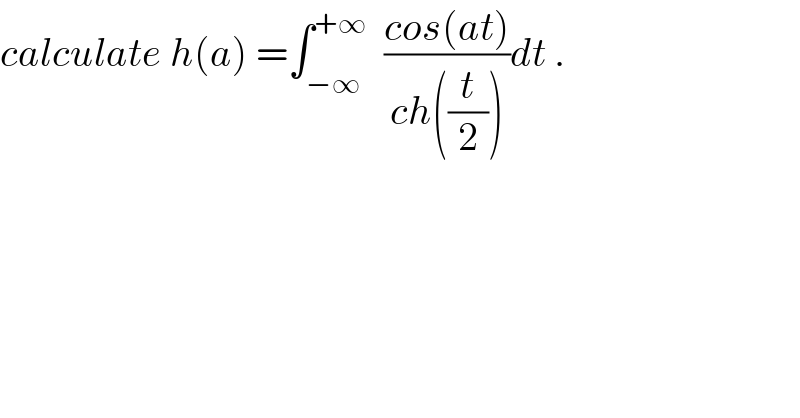 | ||
Commented by Abdo msup. last updated on 08/Feb/19 | ||
![h(a)=_((t/2)=x) 2 ∫_(−∞) ^(+∞) ((cos(2ax))/(ch(x)))dx =4 ∫_0 ^∞ ((cos(2ax))/((e^x +e^(−x) )/2))dx =8 ∫_0 ^∞ ((e^(−x) cos(2ax))/(1+e^(−2x) ))dx =8 ∫_0 ^∞ e^(−x) cos(2ax)(Σ_(n=0) ^∞ (−1)^n e^(−2nx) )dx =8 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)x) cos(2ax)dx let A_n =∫_0 ^∞ e^(−(2n+1)x) cos(2ax)dx ⇒ A_n =Re( ∫_0 ^∞ e^(−(2n+1)x) e^(2iax) dx) but ∫_0 ^∞ e^((−(2n+1)+2ia)x) dx=[(1/(−(2n+1)+2ia)) e^((−(2n+1)+2ia)x) ]_0 ^(+∞) = (1/(−(2n+1)+2ia)) =−(1/((2n+1)−2ia)) =−((2n+1 +2ia)/((2n+1)^2 +4a^2 )) ⇒ A_n =−((2n+1)/((2n+1)^2 +4a^2 )) ⇒ h(a)=8 Σ_(n=0) ^∞ (−1)^(n+1) ((2n+1)/((2n+1)^2 +4a^2 )) and this serie can be calculated by fourier series ...be continued...](Q54638.png) | ||