Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 54376 by Abdo msup. last updated on 02/Feb/19

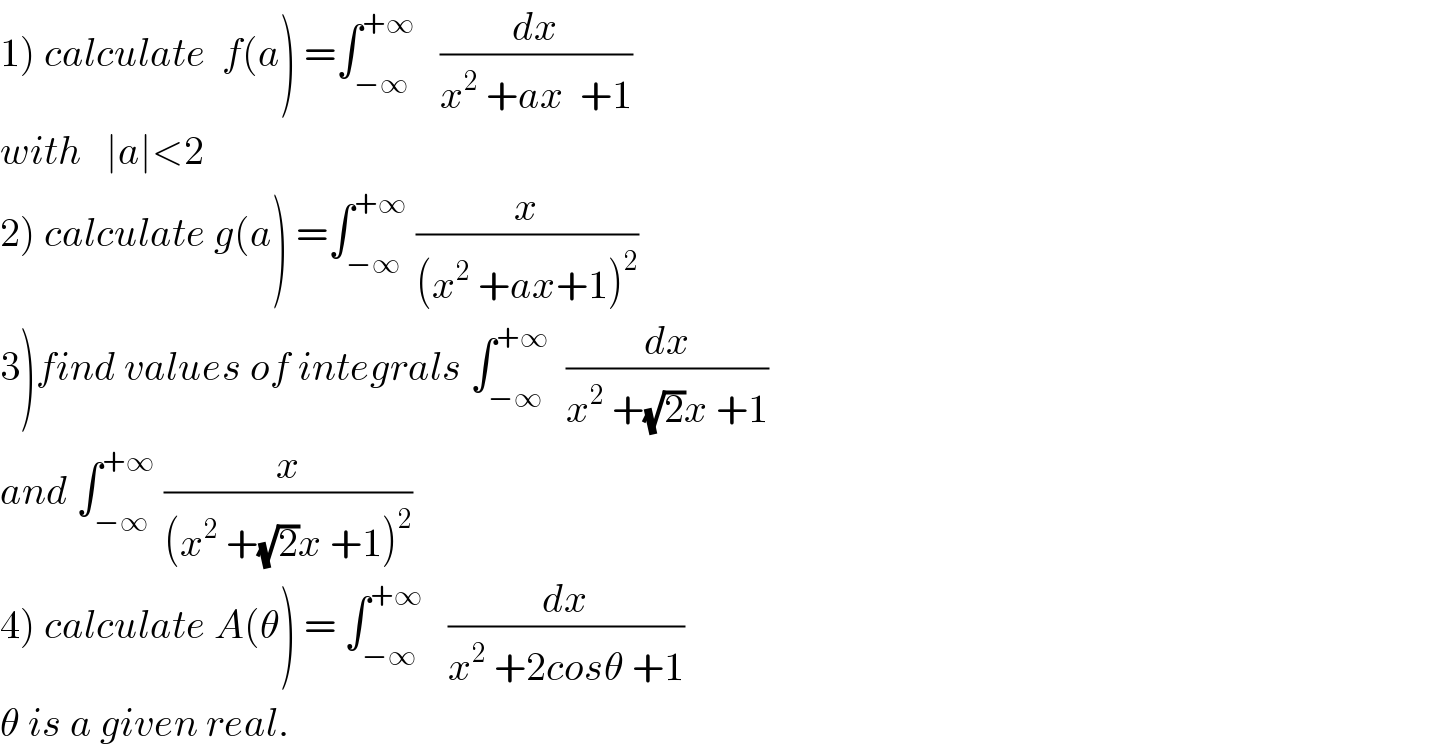
1) calculate f(a) =∫_(−∞) ^(+∞) (dx/(x^2 +ax +1)) with ∣a∣<2 2) calculate g(a) =∫_(−∞) ^(+∞) (x/((x^2 +ax+1)^2 )) 3)find values of integrals ∫_(−∞) ^(+∞) (dx/(x^2 +(√2)x +1)) and ∫_(−∞) ^(+∞) (x/((x^2 +(√2)x +1)^2 )) 4) calculate A(θ) = ∫_(−∞) ^(+∞) (dx/(x^2 +2cosθ +1)) θ is a given real.

$$\left.\mathrm{1}\right)\:{calculate}\:\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{ax}\:\:+\mathrm{1}} \\ $$ $${with}\:\:\:\mid{a}\mid<\mathrm{2} \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:{g}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{x}}{\left({x}^{\mathrm{2}} \:+{ax}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{3}\right){find}\:{values}\:{of}\:{integrals}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}} \\ $$ $${and}\:\int_{−\infty} ^{+\infty} \:\frac{{x}}{\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{4}\right)\:{calculate}\:{A}\left(\theta\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{cos}\theta\:+\mathrm{1}} \\ $$ $$\theta\:{is}\:{a}\:{given}\:{real}. \\ $$

Commented bymaxmathsup by imad last updated on 03/Feb/19

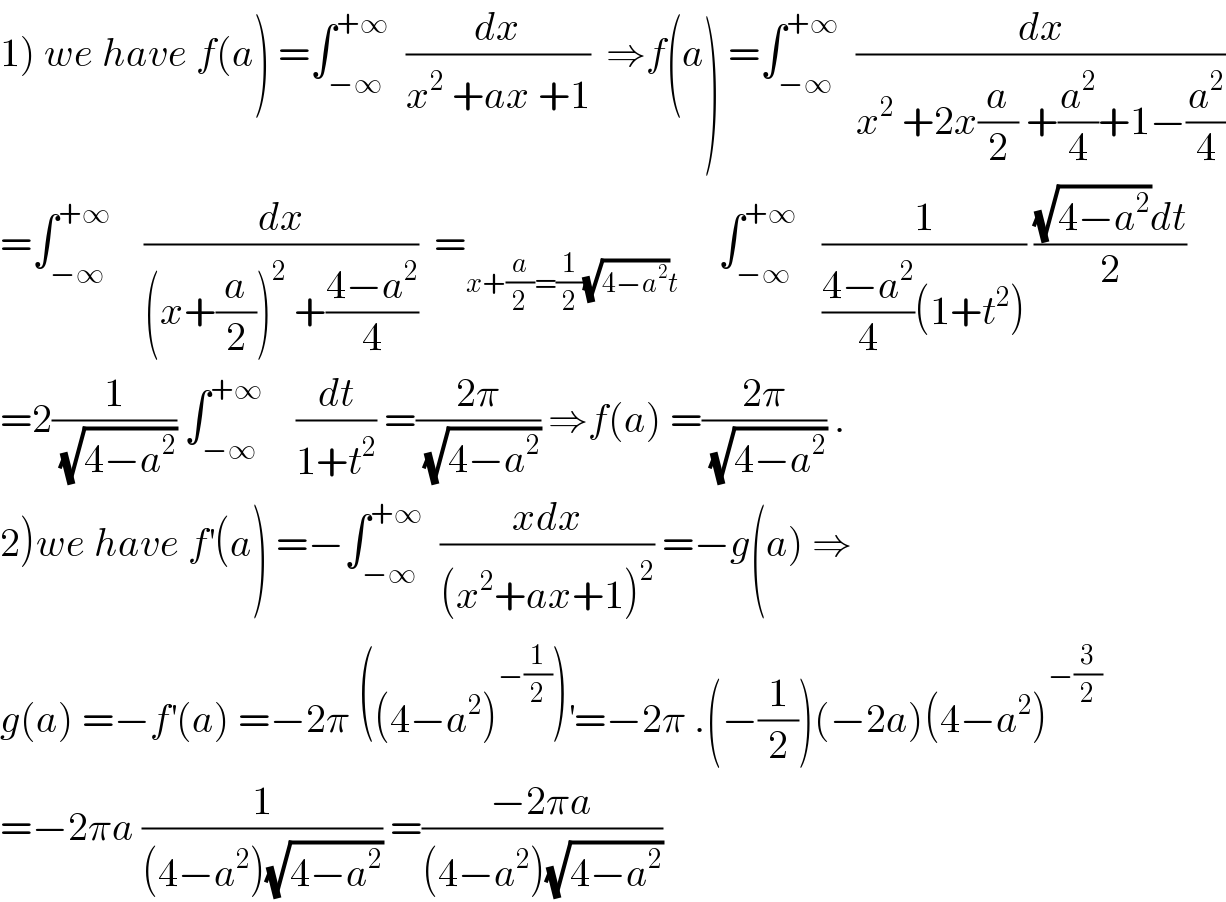
1) we have f(a) =∫_(−∞) ^(+∞) (dx/(x^2 +ax +1)) ⇒f(a) =∫_(−∞) ^(+∞) (dx/(x^2 +2x(a/2) +(a^2 /4)+1−(a^2 /4))) =∫_(−∞) ^(+∞) (dx/((x+(a/2))^2 +((4−a^2 )/4))) =_(x+(a/2)=(1/2)(√(4−a^2 ))t) ∫_(−∞) ^(+∞) (1/(((4−a^2 )/4)(1+t^2 ))) (((√(4−a^2 ))dt)/2) =2(1/(√(4−a^2 ))) ∫_(−∞) ^(+∞) (dt/(1+t^2 )) =((2π)/(√(4−a^2 ))) ⇒f(a) =((2π)/(√(4−a^2 ))) . 2)we have f^′ (a) =−∫_(−∞) ^(+∞) ((xdx)/((x^2 +ax+1)^2 )) =−g(a) ⇒ g(a) =−f^′ (a) =−2π ((4−a^2 )^(−(1/2)) )^′ =−2π .(−(1/2))(−2a)(4−a^2 )^(−(3/2)) =−2πa (1/((4−a^2 )(√(4−a^2 )))) =((−2πa)/((4−a^2 )(√(4−a^2 ))))

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{ax}\:+\mathrm{1}}\:\:\Rightarrow{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}\frac{{a}}{\mathrm{2}}\:+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$ $$=\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}}\:\:=_{{x}+\frac{{a}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }{t}} \:\:\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }{dt}}{\mathrm{2}} \\ $$ $$=\mathrm{2}\frac{\mathrm{1}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\:\Rightarrow{f}\left({a}\right)\:=\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\:. \\ $$ $$\left.\mathrm{2}\right){we}\:{have}\:{f}^{'} \left({a}\right)\:=−\int_{−\infty} ^{+\infty} \:\:\frac{{xdx}}{\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)^{\mathrm{2}} }\:=−{g}\left({a}\right)\:\Rightarrow \\ $$ $${g}\left({a}\right)\:=−{f}^{'} \left({a}\right)\:=−\mathrm{2}\pi\:\left(\left(\mathrm{4}−{a}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{'} =−\mathrm{2}\pi\:.\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\mathrm{2}{a}\right)\left(\mathrm{4}−{a}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$ $$=−\mathrm{2}\pi{a}\:\frac{\mathrm{1}}{\left(\mathrm{4}−{a}^{\mathrm{2}} \right)\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\:=\frac{−\mathrm{2}\pi{a}}{\left(\mathrm{4}−{a}^{\mathrm{2}} \right)\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }} \\ $$

Commented bymaxmathsup by imad last updated on 03/Feb/19

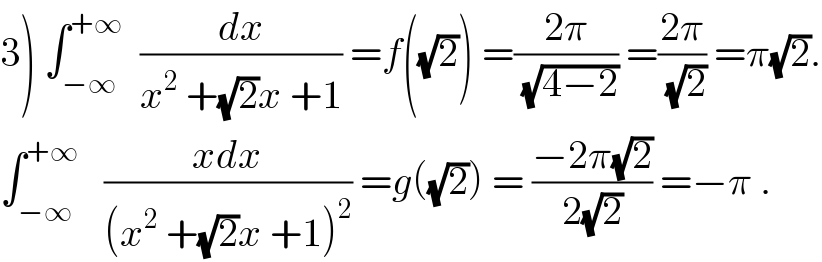
3) ∫_(−∞) ^(+∞) (dx/(x^2 +(√2)x +1)) =f((√2)) =((2π)/(√(4−2))) =((2π)/(√2)) =π(√2). ∫_(−∞) ^(+∞) ((xdx)/((x^2 +(√2)x +1)^2 )) =g((√2)) = ((−2π(√2))/(2(√2))) =−π .

$$\left.\mathrm{3}\right)\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\:={f}\left(\sqrt{\mathrm{2}}\right)\:=\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}−\mathrm{2}}}\:=\frac{\mathrm{2}\pi}{\sqrt{\mathrm{2}}}\:=\pi\sqrt{\mathrm{2}}. \\ $$ $$\int_{−\infty} ^{+\infty} \:\:\:\frac{{xdx}}{\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\:={g}\left(\sqrt{\mathrm{2}}\right)\:=\:\frac{−\mathrm{2}\pi\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=−\pi\:. \\ $$

Commented bymaxmathsup by imad last updated on 03/Feb/19

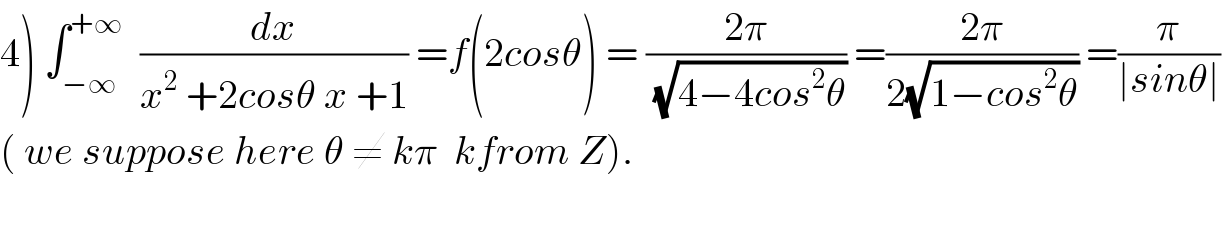
4) ∫_(−∞) ^(+∞) (dx/(x^2 +2cosθ x +1)) =f(2cosθ) = ((2π)/(√(4−4cos^2 θ))) =((2π)/(2(√(1−cos^2 θ)))) =(π/(∣sinθ∣)) ( we suppose here θ ≠ kπ kfrom Z).

$$\left.\mathrm{4}\right)\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{cos}\theta\:{x}\:+\mathrm{1}}\:={f}\left(\mathrm{2}{cos}\theta\right)\:=\:\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}−\mathrm{4}{cos}^{\mathrm{2}} \theta}}\:=\frac{\mathrm{2}\pi}{\mathrm{2}\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \theta}}\:=\frac{\pi}{\mid{sin}\theta\mid} \\ $$ $$\left(\:{we}\:{suppose}\:{here}\:\theta\:\neq\:{k}\pi\:\:{kfrom}\:{Z}\right). \\ $$ $$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

2)(1/2)∫((2x+a−a)/((x^2 +ax+1)^2 ))dx (1/2)∫((d(x^2 +ax+1))/((x^2 +ax+1)^2 ))dx−(a/2)∫(dx/([(x+(a/2))^2 +((√(1−(a^2 /4))) )^2 ]^2 )) (1/2)×((−1)/((x^2 +ax+1)))−(a/2)I_2 I_2 let (x+(a/2))=(√(1−(a^2 /4))) tanθ=ktanθ dx=k sec^2 θdθ so I_2 =∫((ksec^2 θdθ)/([k^2 tan^2 θ+k^2 ]^2 )) ∫((ksec^2 θ)/(k^4 sec^4 θ))dθ (1/k^3 )∫(((1+cos2θ)/2))dθ (1/(2k^3 ))θ+(1/(4k^3 ))sin2θ+c (1/(2k^3 ))tan^(−1) (((x+(a/2))/k))+(1/(4k^3 ))×((2(((x+(a/2))/k)))/(1+(((x+(a/2))/k))^2 ))+c so ((−1)/(2(x^2 +ax+1)))−(a/2)[(1/(2k^3 ))tan^(−1) (((x+(a/2))/k))+(1/(2k^3 ))×(((((x+(a/2))/k)))/(1+(((x+(a/2))/k))^2 ))] ∣((−1)/(2(x^2 +ax+1)))−(a/(4k^3 ))[tan^(−1) (((x+(a/2))/k))+(((x+(a/2))/k)/(1+(((x+(a/2))/k))^2 ))]∣_(−∞) ^∞ =0−(a/(4k^3 ))[{tan^(−1) (∞)−tan^(−1) (−∞)}+0] =−(a/(4k^3 ))×(π/1)=((−aπ)/(4(1−(a^2 /4))^(3/2) )) 3)second part =((−(√2) π)/(4(1−(1/2))^(3/2) ))=((−(√2) π)/4)×(√2) ×(√2) ×(√2) =−π answer

$$\left.\mathrm{2}\right)\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}+{a}−{a}}{\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)^{\mathrm{2}} }{dx}−\frac{{a}}{\mathrm{2}}\int\frac{{dx}}{\left[\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:\right)^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}}×\frac{−\mathrm{1}}{\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)}−\frac{{a}}{\mathrm{2}}{I}_{\mathrm{2}} \\ $$ $${I}_{\mathrm{2}} \:\:{let}\:\left({x}+\frac{{a}}{\mathrm{2}}\right)=\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:{tan}\theta={ktan}\theta \\ $$ $${dx}={k}\:{sec}^{\mathrm{2}} \theta{d}\theta \\ $$ $${so}\:{I}_{\mathrm{2}} =\int\frac{{ksec}^{\mathrm{2}} \theta{d}\theta}{\left[{k}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$ $$\int\frac{{ksec}^{\mathrm{2}} \theta}{{k}^{\mathrm{4}} {sec}^{\mathrm{4}} \theta}{d}\theta \\ $$ $$\frac{\mathrm{1}}{{k}^{\mathrm{3}} }\int\left(\frac{\mathrm{1}+{cos}\mathrm{2}\theta}{\mathrm{2}}\right){d}\theta \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{3}} }\theta+\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{3}} }{sin}\mathrm{2}\theta+{c} \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{3}} }{tan}^{−\mathrm{1}} \left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)+\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{3}} }×\frac{\mathrm{2}\left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)}{\mathrm{1}+\left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)^{\mathrm{2}} }+{c} \\ $$ $${so}\: \\ $$ $$\frac{−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)}−\frac{{a}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{3}} }{tan}^{−\mathrm{1}} \left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)+\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{3}} }×\frac{\left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)}{\mathrm{1}+\left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)^{\mathrm{2}} }\right] \\ $$ $$\mid\frac{−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)}−\frac{{a}}{\mathrm{4}{k}^{\mathrm{3}} }\left[{tan}^{−\mathrm{1}} \left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)+\frac{\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}}{\mathrm{1}+\left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{{k}}\right)^{\mathrm{2}} }\right]\mid_{−\infty} ^{\infty} \\ $$ $$=\mathrm{0}−\frac{{a}}{\mathrm{4}{k}^{\mathrm{3}} }\left[\left\{{tan}^{−\mathrm{1}} \left(\infty\right)−{tan}^{−\mathrm{1}} \left(−\infty\right)\right\}+\mathrm{0}\right] \\ $$ $$=−\frac{{a}}{\mathrm{4}{k}^{\mathrm{3}} }×\frac{\pi}{\mathrm{1}}=\frac{−{a}\pi}{\mathrm{4}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$ $$ \\ $$ $$\left.\mathrm{3}\right){second}\:{part}\:=\frac{−\sqrt{\mathrm{2}}\:\pi}{\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{−\sqrt{\mathrm{2}}\:\pi}{\mathrm{4}}×\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:=−\pi\:{answer} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

1)∫(dx/(x^2 +2x(a/2)+(a^2 /4)+1−(a^2 /4)))dx ∫(dx/(((√(1−(a^2 /4))) )^2 +(x+(a/2))^2 )) so answer is ∣(1/((√(1−(a^2 /4))) ))tan^(−1) (((x+(a/2))/(√(1−(a^2 /4)))))∣_(−∞) ^∞ [(a^2 /4)<1] =(1/(√(1−(a^2 /4))))×{(π/2)−(−(π/2))}=(π/(√(1−(a^2 /4)))) 3)(π/(√(1−(2/4))))=π(√2)

$$\left.\mathrm{1}\right)\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}\frac{{a}}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}{dx} \\ $$ $$\int\frac{{dx}}{\left(\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:\right)^{\mathrm{2}} +\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$ $${so}\:{answer}\:{is} \\ $$ $$\mid\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:}{tan}^{−\mathrm{1}} \left(\frac{{x}+\frac{{a}}{\mathrm{2}}}{\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}\right)\mid_{−\infty} ^{\infty} \:\left[\frac{{a}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{1}\right] \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}×\left\{\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right\}=\frac{\pi}{\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$ $$\left.\mathrm{3}\right)\frac{\pi}{\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{4}}}}=\pi\sqrt{\mathrm{2}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

4)∫_(−∞) ^∞ (dx/(x^2 +b^2 )) [[[b^2 =1+2cosθ] (1/b)∣tan^(−1) ((x/b))∣_(−∞) ^∞ (1/b)[tan^(−1) (∞)−tan^(−1) (−∞)] =(1/(√(1+2cosθ)))×{(π/2)−((−π)/2)} =(π/(√(1+2cosθ)))

$$\left.\mathrm{4}\right)\int_{−\infty} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\left[\left[\left[{b}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{cos}\theta\right]\right.\right. \\ $$ $$\frac{\mathrm{1}}{{b}}\mid{tan}^{−\mathrm{1}} \left(\frac{{x}}{{b}}\right)\mid_{−\infty} ^{\infty} \\ $$ $$\frac{\mathrm{1}}{{b}}\left[{tan}^{−\mathrm{1}} \left(\infty\right)−{tan}^{−\mathrm{1}} \left(−\infty\right)\right] \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{2}{cos}\theta}}×\left\{\frac{\pi}{\mathrm{2}}−\frac{−\pi}{\mathrm{2}}\right\} \\ $$ $$=\frac{\pi}{\sqrt{\mathrm{1}+\mathrm{2}{cos}\theta}} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com