
Question and Answers Forum
Question Number 54420 by gunawan last updated on 03/Feb/19
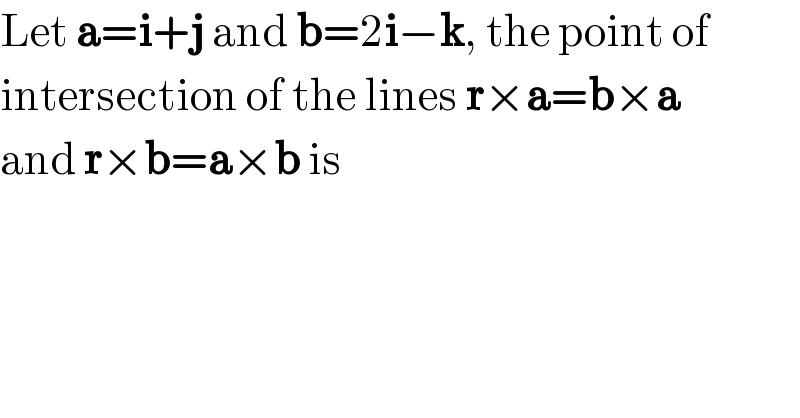
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19
![r=ix+jy+kz r×a=[i j k ] =i(0−z)−j(0−z)+k(x−y) [x y z ] [1 1 0] b×a=[i j k ]=i(0+1)−j(0+1)+k(2) [2 0 −1] [1 1 0] so (−z)=1 (−z)=1 x−y=2 [ z=−1]] r×b=[i j k ]=i(−y−0)−j(−x−2z)+k(0−2y) [x y z ] [2 0 −1] a×b=−(b×a)=−i+j−2k so −y=−1 [y=1] x+2z=1 x=1−2(−1)=3 x−y=2 x=2+1=3 [x=3 y=1 z=−1] r=3i+j−k pls write question clearly....](Q54434.png)
| ||
Question and Answers Forum | ||
Question Number 54420 by gunawan last updated on 03/Feb/19 | ||
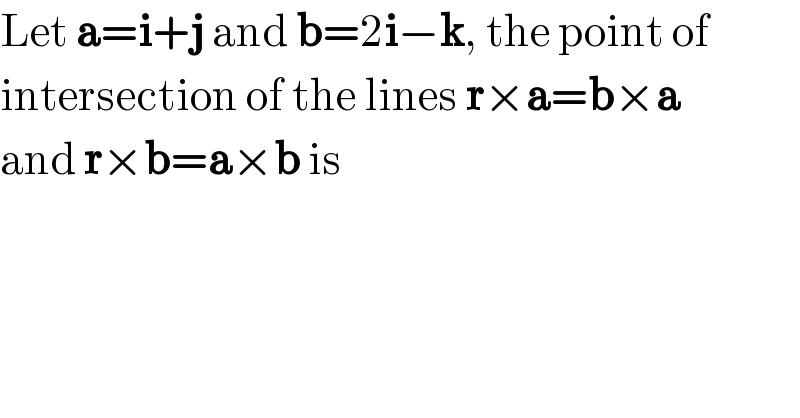 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19 | ||
![r=ix+jy+kz r×a=[i j k ] =i(0−z)−j(0−z)+k(x−y) [x y z ] [1 1 0] b×a=[i j k ]=i(0+1)−j(0+1)+k(2) [2 0 −1] [1 1 0] so (−z)=1 (−z)=1 x−y=2 [ z=−1]] r×b=[i j k ]=i(−y−0)−j(−x−2z)+k(0−2y) [x y z ] [2 0 −1] a×b=−(b×a)=−i+j−2k so −y=−1 [y=1] x+2z=1 x=1−2(−1)=3 x−y=2 x=2+1=3 [x=3 y=1 z=−1] r=3i+j−k pls write question clearly....](Q54434.png) | ||
| ||