Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 54447 by ajfour last updated on 03/Feb/19

Commented by ajfour last updated on 14/Feb/19

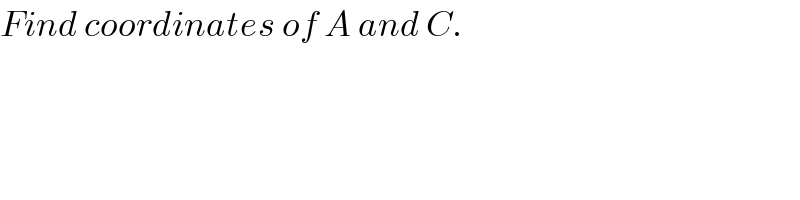
Find coordinates of A and C.

$${Find}\:{coordinates}\:{of}\:{A}\:{and}\:{C}.\:\:\:\:\:\:\:\: \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

solve x^2 =ry and (x−r)^2 +(y−r)^2 =r^2 (x−r)^2 +((x^2 /r)−r)^2 =r^2 x^2 −2xr+r^2 +(x^4 /r^2 )−2x^2 +r^2 =r^2 (x^4 /r^2 )−x^2 −2xr+r^2 =0 x^4 −r^2 x^2 −2xr^3 +r^4 =0 on solving we get four value of x so corresponding four value of y thus we can get co iridinate of point A and C ok le t try to solve... let (x/r)=k (x^4 /r^4 )−(x^2 /r^2 )−((2x)/r)+1=0 k^4 −k^2 −2k+1=0 f(k)=k^4 −k^2 −2k+1=k^4 −k^2 −2k−1+2=k^4 +2−(k+1)^2 f(0)>0 f(1)<0 f(0.5)=(1/(16))−(1/4)−(2/2)+1<0 f(0.4)=0.0256+2−1.96>0 so value of [0.5 >k>0.4] thus 0.5>(x/r)>0.4 so 0.5r>x>0.4r thus x=(0.4+ε)r ε=is a small number...

$${solve}\:\:{x}^{\mathrm{2}} ={ry}\:{and}\:\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +\left(\frac{{x}^{\mathrm{2}} }{{r}}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xr}+{r}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{{r}^{\mathrm{2}} }−\mathrm{2}{x}^{\mathrm{2}} +{r}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{4}} }{{r}^{\mathrm{2}} }−{x}^{\mathrm{2}} −\mathrm{2}{xr}+{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} −{r}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{xr}^{\mathrm{3}} +{r}^{\mathrm{4}} =\mathrm{0} \\ $$$${on}\:{solving}\:\:{we}\:{get}\:{four}\:{value}\:{of}\:{x} \\ $$$${so}\:{corresponding}\:{four}\:{value}\:{of}\:{y} \\ $$$${thus}\:{we}\:{can}\:{get}\:{co}\:{iridinate}\:{of}\:\:{point}\:{A}\:{and}\:{C} \\ $$$${ok}\:{le}\:{t}\:{try}\:{to}\:{solve}... \\ $$$${let}\:\frac{{x}}{{r}}={k} \\ $$$$\frac{{x}^{\mathrm{4}} }{{r}^{\mathrm{4}} }−\frac{{x}^{\mathrm{2}} }{{r}^{\mathrm{2}} }−\frac{\mathrm{2}{x}}{{r}}+\mathrm{1}=\mathrm{0} \\ $$$${k}^{\mathrm{4}} −{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}=\mathrm{0} \\ $$$${f}\left({k}\right)={k}^{\mathrm{4}} −{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}={k}^{\mathrm{4}} −{k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{1}+\mathrm{2}={k}^{\mathrm{4}} +\mathrm{2}−\left({k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${f}\left(\mathrm{0}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{5}\right)=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{2}}{\mathrm{2}}+\mathrm{1}<\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{4}\right)=\mathrm{0}.\mathrm{0256}+\mathrm{2}−\mathrm{1}.\mathrm{96}>\mathrm{0} \\ $$$${so}\:{value}\:{of}\:\left[\mathrm{0}.\mathrm{5}\:>{k}>\mathrm{0}.\mathrm{4}\right] \\ $$$${thus}\:\:\:\:\mathrm{0}.\mathrm{5}>\frac{{x}}{{r}}>\mathrm{0}.\mathrm{4} \\ $$$${so}\:\:\:\mathrm{0}.\mathrm{5}{r}>{x}>\mathrm{0}.\mathrm{4}{r} \\ $$$${thus}\:\:{x}=\left(\mathrm{0}.\mathrm{4}+\epsilon\right){r}\:\:\:\epsilon={is}\:{a}\:{small}\:{number}... \\ $$

Commented by ajfour last updated on 03/Feb/19

why not solve it, Sir ?

$${why}\:{not}\:{solve}\:{it},\:{Sir}\:? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19

i can not solve without numirical value.. if numirical value present i can use calculus.. but general eqn...i can not solve...

$${i}\:{can}\:{not}\:{solve}\:{without}\:{numirical}\:{value}.. \\ $$$${if}\:{numirical}\:{value}\:{present}\:{i}\:{can}\:{use}\:{calculus}.. \\ $$$${but}\:{general}\:{eqn}...{i}\:{can}\:{not}\:{solve}... \\ $$

Commented by ajfour last updated on 03/Feb/19

it can be converted to one like numerical value, but still let us not use calculator.

$${it}\:{can}\:{be}\:{converted}\:{to}\:{one}\:{like} \\ $$$${numerical}\:{value},\:{but}\:{still}\:{let}\:{us}\:{not} \\ $$$${use}\:{calculator}. \\ $$

Commented by ajfour last updated on 03/Feb/19

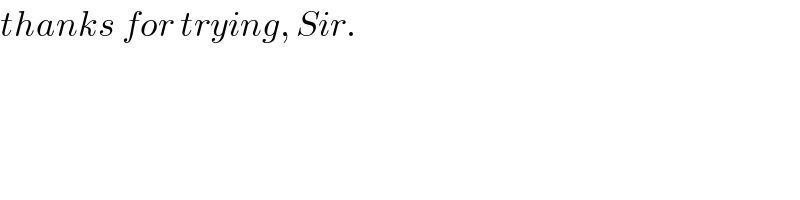
thanks for trying, Sir.

$${thanks}\:{for}\:{trying},\:{Sir}. \\ $$

Answered by ajfour last updated on 04/Feb/19

(x−r)^2 +(y−r)^2 =r^2 (circle eq.) y=x^2 /r (parabola eq.) for x= x_A , x_C x^2 −2rx+(x^4 /r^2 )−2x^2 +r^2 =0 (x^4 /r^2 )−x^2 −2rx+r^2 =0 if x/r =t ⇒ t^4 −t^2 −2t+1=0 ....(i) let us assume equivalently (t^2 −pt+q)(t^2 +pt+(1/q))=0 ⇒ t^4 +(q+(1/q)−p^2 )t^2 +(pq−(p/q))t+1=0 comparing with (i) q+(1/q)= p^2 −1 and q−(1/q)=−(2/p) ⇒ (p^2 −1)^2 −(4/p^2 ) = 4 let us call p^2 =s ⇒ s(s−1)^2 −4s−4=0 let s−1= u ⇒ (u+1)u^2 −4(u+2)=0 ⇒ u^3 +u^2 −4u−8=0 let u=z−1/3 ⇒ z^3 −z^2 _− +(z/3)−(1/(27))+z^2 _− −((2z)/3)+(1/9) −4z+(4/3)−8=0 or z^3 −((13)/3)z−((178)/(27))=0 z= (((89)/(27))+(√(((89^2 )/(27^2 ))−((13^3 )/(27^2 )))) )^(1/3) +(((89)/(27))−(√((((89)/(27^2 ))−((13^3 )/(27^2 )))) )^(1/3) =(1/3){(89+6(√(159)))^(1/3) +(89−6(√(159)))^(1/3) now p^2 =s=u+1 = z+(2/3) since t_A >0 and t_C >0 let′s first choose (t^2 −pt+q)=0 with p_1 >0 p_1 =(√((2+(89+6(√(159)))^(1/3) +(89−6(√(159)))^(1/3) )/3)) ≈ 1.81226 (D/4)= (p^2 /4)−q as q= (((p^2 −1))/2)−(1/p) (D/4)=(1/2)+(1/p)−(p^2 /4) ≈ 0.23073 if it is positive then __________________________ with p_1 =(√((2+(89+6(√(159)))^(1/3) +(89−6(√(159)))^(1/3) )/3)) x_A =r( (p_1 /2)−(√((1/2)+(1/p_1 )−(p_1 ^2 /4)))) ⇒ x_A ≈ 0.4258 r , y_A =x_A ^2 /r x_C =r( (p_1 /2)+(√((1/2)+(1/p_1 )−(p_1 ^2 /4)))) ⇒ x_C ≈ 1.3865 r , y_C =x_C ^2 /r __________________________■

$$\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:\:\left({circle}\:{eq}.\right) \\ $$$${y}={x}^{\mathrm{2}} /{r}\:\:\:\:\:\:\:\:\:\:\:\:\:\left({parabola}\:{eq}.\right) \\ $$$${for}\:{x}=\:{x}_{{A}} ,\:{x}_{{C}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{rx}+\frac{{x}^{\mathrm{4}} }{{r}^{\mathrm{2}} }−\mathrm{2}{x}^{\mathrm{2}} +{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\frac{{x}^{\mathrm{4}} }{{r}^{\mathrm{2}} }−{x}^{\mathrm{2}} −\mathrm{2}{rx}+{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${if}\:\:\:{x}/{r}\:={t} \\ $$$$\:\Rightarrow\:\:\:{t}^{\mathrm{4}} −{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}=\mathrm{0}\:\:\:\:\:\:....\left({i}\right) \\ $$$${let}\:{us}\:{assume}\:{equivalently} \\ $$$$\:\:\:\:\:\left({t}^{\mathrm{2}} −{pt}+{q}\right)\left({t}^{\mathrm{2}} +{pt}+\frac{\mathrm{1}}{{q}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}^{\mathrm{4}} +\left({q}+\frac{\mathrm{1}}{{q}}−{p}^{\mathrm{2}} \right){t}^{\mathrm{2}} +\left({pq}−\frac{{p}}{{q}}\right){t}+\mathrm{1}=\mathrm{0} \\ $$$${comparing}\:{with}\:\left({i}\right) \\ $$$$\:\:\:\:\boldsymbol{{q}}+\frac{\mathrm{1}}{\boldsymbol{{q}}}=\:\boldsymbol{{p}}^{\mathrm{2}} −\mathrm{1}\:\:\:{and}\:\:\boldsymbol{{q}}−\frac{\mathrm{1}}{\boldsymbol{{q}}}=−\frac{\mathrm{2}}{\boldsymbol{{p}}} \\ $$$$\Rightarrow\:\:\left({p}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{4}}{{p}^{\mathrm{2}} }\:=\:\mathrm{4} \\ $$$${let}\:{us}\:{call}\:\:{p}^{\mathrm{2}} ={s} \\ $$$$\Rightarrow\:\:{s}\left({s}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{s}−\mathrm{4}=\mathrm{0} \\ $$$${let}\:{s}−\mathrm{1}=\:{u} \\ $$$$\Rightarrow\:\:\left({u}+\mathrm{1}\right){u}^{\mathrm{2}} −\mathrm{4}\left({u}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{4}{u}−\mathrm{8}=\mathrm{0} \\ $$$${let}\:\:{u}={z}−\mathrm{1}/\mathrm{3} \\ $$$$\Rightarrow\:\:{z}^{\mathrm{3}} −\underset{−} {{z}}^{\mathrm{2}} +\frac{{z}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{27}}+\underset{−} {{z}}^{\mathrm{2}} −\frac{\mathrm{2}{z}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{z}+\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{8}=\mathrm{0} \\ $$$${or}\:\:\:{z}^{\mathrm{3}} −\frac{\mathrm{13}}{\mathrm{3}}{z}−\frac{\mathrm{178}}{\mathrm{27}}=\mathrm{0} \\ $$$$\:\:\:\:{z}=\:\left(\frac{\mathrm{89}}{\mathrm{27}}+\sqrt{\frac{\mathrm{89}^{\mathrm{2}} }{\mathrm{27}^{\mathrm{2}} }−\frac{\mathrm{13}^{\mathrm{3}} }{\mathrm{27}^{\mathrm{2}} }}\:\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\frac{\mathrm{89}}{\mathrm{27}}−\sqrt{\left(\frac{\mathrm{89}}{\mathrm{27}^{\mathrm{2}} }−\frac{\mathrm{13}^{\mathrm{3}} }{\mathrm{27}^{\mathrm{2}} }\right.}\:\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left\{\left(\mathrm{89}+\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{89}−\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} \right. \\ $$$${now}\:\:\:{p}^{\mathrm{2}} ={s}={u}+\mathrm{1}\:=\:{z}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${since}\:{t}_{{A}} >\mathrm{0}\:{and}\:{t}_{{C}} \:>\mathrm{0} \\ $$$${let}'{s}\:{first}\:{choose}\:\:\left({t}^{\mathrm{2}} −{pt}+{q}\right)=\mathrm{0} \\ $$$${with}\:{p}_{\mathrm{1}} >\mathrm{0}\: \\ $$$${p}_{\mathrm{1}} =\sqrt{\frac{\mathrm{2}+\left(\mathrm{89}+\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{89}−\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} }{\mathrm{3}}} \\ $$$$\:\:\:\:\approx\:\mathrm{1}.\mathrm{81226} \\ $$$$\frac{{D}}{\mathrm{4}}=\:\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}\: \\ $$$$\:{as}\:\:{q}=\:\frac{\left({p}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{1}}{{p}} \\ $$$$\frac{{D}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{p}}−\frac{{p}^{\mathrm{2}} }{\mathrm{4}}\:\approx\:\mathrm{0}.\mathrm{23073} \\ $$$${if}\:{it}\:{is}\:{positive}\:{then} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${with}\: \\ $$$${p}_{\mathrm{1}} =\sqrt{\frac{\mathrm{2}+\left(\mathrm{89}+\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{89}−\mathrm{6}\sqrt{\mathrm{159}}\right)^{\mathrm{1}/\mathrm{3}} }{\mathrm{3}}} \\ $$$$\:\:{x}_{{A}} ={r}\left(\:\frac{{p}_{\mathrm{1}} }{\mathrm{2}}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{p}_{\mathrm{1}} }−\frac{{p}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}}\right) \\ $$$$\Rightarrow\:\:{x}_{{A}} \approx\:\mathrm{0}.\mathrm{4258}\:{r}\:\:\:,\:\:\:{y}_{{A}} ={x}_{{A}} ^{\mathrm{2}} /{r} \\ $$$$\:\:\:\:\:\:{x}_{{C}} ={r}\left(\:\frac{{p}_{\mathrm{1}} }{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{p}_{\mathrm{1}} }−\frac{{p}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}}\right) \\ $$$$\Rightarrow\:\:{x}_{{C}} \:\approx\:\mathrm{1}.\mathrm{3865}\:{r}\:\:\:,\:\:\:\:{y}_{{C}} ={x}_{{C}} ^{\mathrm{2}} /{r}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\blacksquare \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com