Question Number 54585 by peter frank last updated on 07/Feb/19
$${show}\:{that}\:\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{6}} }{dx}=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
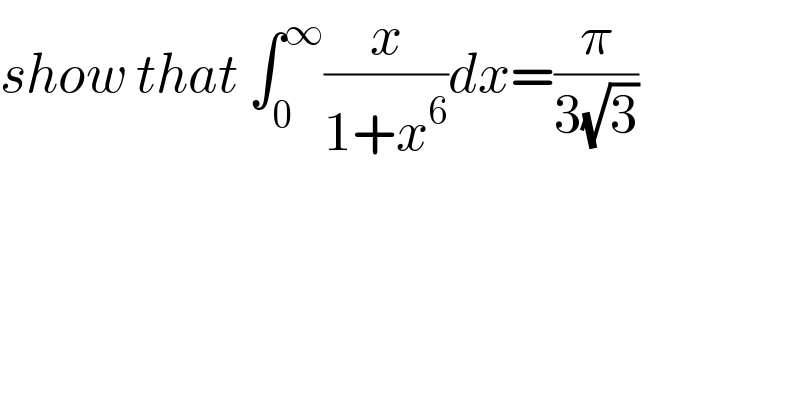
Commented by maxmathsup by imad last updated on 07/Feb/19
$${let}\:\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:\:\:{changement}\:\:{x}^{\mathrm{6}} ={t}\:{give}\:{x}\:={t}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{6}}} }{\mathrm{1}+{t}}\:\frac{\mathrm{1}}{\mathrm{6}}\:{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt}\:\:{but}\:{we}\:{have}\:{proved}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:\:\:{with}\:\mathrm{0}<{a}<\mathrm{1}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\pi}{\mathrm{6}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:. \\ $$
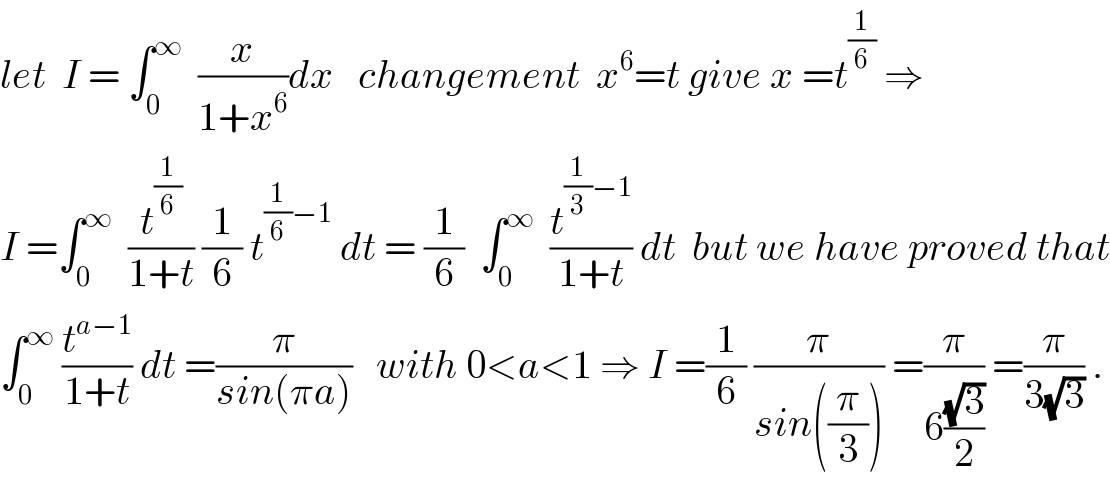
Answered by arvinddayama00@gmail.com last updated on 08/Feb/19
$${x}^{\mathrm{2}} ={t}\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{0},{t}=\mathrm{0} \\ $$$$\mathrm{2}{xdx}={dt}\:\:\:{x}=\infty,{t}=\infty\:\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}\:} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{3}} } \\ $$$$\because\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\alpha} }=\frac{\pi}{\alpha{sin}\left(\frac{\pi}{\alpha}\right)}\bigstar\bigstar \\ $$$${so}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{3}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${pls}..\:{cheak}..... \\ $$$$\:\:\:\:\: \\ $$
Commented by peter frank last updated on 07/Feb/19
$${right}\:{sir} \\ $$
Commented by rahul 19 last updated on 08/Feb/19
$${Sir},\:{how}\:\int_{\mathrm{0}} ^{\:\infty} \frac{{dx}}{\mathrm{1}+{x}^{\alpha} }\:=\:\frac{\pi}{\alpha\mathrm{sin}\:\left(\frac{\pi}{\alpha}\right)}\:? \\ $$
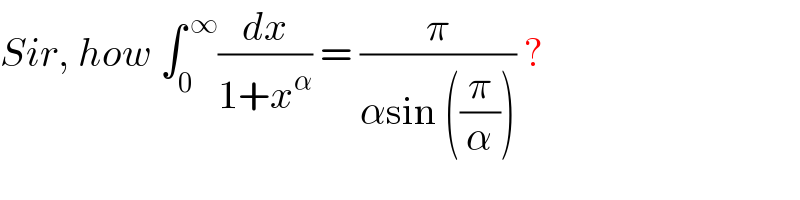
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Feb/19
![x^α =tan^2 θ x=(tanθ)^(2/α) dx=(2/α)(tanθ)^((2/α)−1) (sec^2 θ)dθ ∫_0 ^(π/2) (2/α)(tanθ)^((2/α)−1) dθ (2/α)∫_0 ^(π/2) (sinθ)^((2/α)−1) (cosθ)^(1−(2/α)) dθ now gamma beta function formula 2∫_0 ^(π/2) (sinθ)^(2p−1) (cosθ)^(2q−1) dθ=((⌈(p)⌈q))/(⌈(p+q))) now here 2p−1=(2/α)−1 so p=(1/α) 2q−1=1−(2/α) so q=(1−(1/α)) now answer is=(1/α)×((⌈((1/α))⌈(1−(1/α)))/(⌈(1)))=(1/α)×(π/(sin((π/α)))) [again formula ⌈(a)⌈(1−a)=(π/(sin(aπ)))]](Q54623.png)
$${x}^{\alpha} ={tan}^{\mathrm{2}} \theta\:\:\:{x}=\left({tan}\theta\right)^{\frac{\mathrm{2}}{\alpha}} \\ $$$${dx}=\frac{\mathrm{2}}{\alpha}\left({tan}\theta\right)^{\frac{\mathrm{2}}{\alpha}−\mathrm{1}} \left({sec}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}}{\alpha}\left({tan}\theta\right)^{\frac{\mathrm{2}}{\alpha}−\mathrm{1}} {d}\theta \\ $$$$\frac{\mathrm{2}}{\alpha}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\frac{\mathrm{2}}{\alpha}−\mathrm{1}} \left({cos}\theta\right)^{\mathrm{1}−\frac{\mathrm{2}}{\alpha}} {d}\theta \\ $$$${now}\:{gamma}\:{beta}\:{function}\:{formula} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\mathrm{2}{p}−\mathrm{1}} \left({cos}\theta\right)^{\mathrm{2}{q}−\mathrm{1}} {d}\theta=\frac{\left.\lceil\left({p}\right)\lceil{q}\right)}{\lceil\left({p}+{q}\right)} \\ $$$${now}\:{here}\:\mathrm{2}{p}−\mathrm{1}=\frac{\mathrm{2}}{\alpha}−\mathrm{1}\:\:{so}\:{p}=\frac{\mathrm{1}}{\alpha} \\ $$$$\mathrm{2}{q}−\mathrm{1}=\mathrm{1}−\frac{\mathrm{2}}{\alpha}\:{so}\:{q}=\left(\mathrm{1}−\frac{\mathrm{1}}{\alpha}\right) \\ $$$${now}\:{answer}\:{is}=\frac{\mathrm{1}}{\alpha}×\frac{\lceil\left(\frac{\mathrm{1}}{\alpha}\right)\lceil\left(\mathrm{1}−\frac{\mathrm{1}}{\alpha}\right)}{\lceil\left(\mathrm{1}\right)}=\frac{\mathrm{1}}{\alpha}×\frac{\pi}{{sin}\left(\frac{\pi}{\alpha}\right)} \\ $$$$\left[{again}\:{formula}\:\lceil\left({a}\right)\lceil\left(\mathrm{1}−{a}\right)=\frac{\pi}{{sin}\left({a}\pi\right)}\right] \\ $$