Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 54699 by rahul 19 last updated on 09/Feb/19

$$\int e^{2x}(\frac{1}{x}-\frac{1}{2x^2})dx$$$$\int e^{2x}\left(\frac{1+\sin 2x}{1+\cos 2x}\right)dx.$$$$SolveaboveQuestionsbyusingthe$$$$formulae:$$$$\int e^{kx}\{f\left(kx\right)+f{}^{\prime }\left(kx\right)\}dx=e^{kx}f\left(kx\right)+c.$$

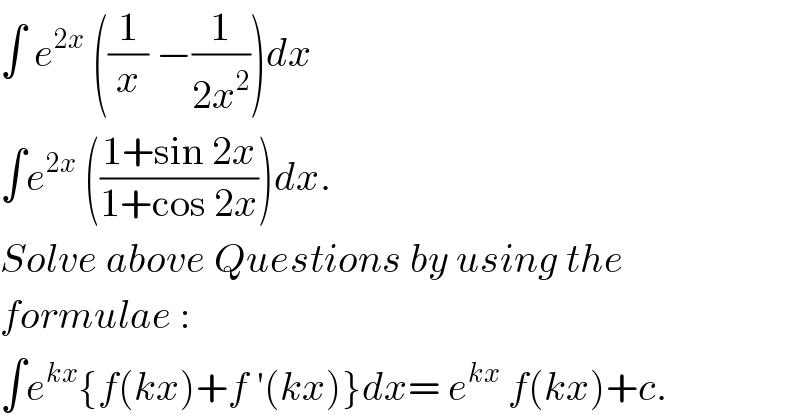
Commented by maxmathsup by imad last updated on 10/Feb/19

$$letI=\int (\frac{1}{x}-\frac{1}{2x^2})e^{2x}dx\Rightarrow I=\int \frac{e^{2x}}{x}dx-\int \frac{e^{2x}}{2x^2}bypsrts$$$$\int \frac{e^{2x}}{x}dx=\frac{1}{2x}{e}^{2x}-\int -\frac{1}{2x^2}{e}^{2x}=\frac{1}{2x}{e}^{2x}+\int \frac{e^{2x}}{2x^2}\Rightarrow$$$$I=\frac{e^{2x}}{2x}+\int \frac{e^{2x}}{2x^2}-\int \frac{e^{2x}}{2x^2}dx+c\Rightarrow I=\frac{e^{2x}}{2x}+c.$$

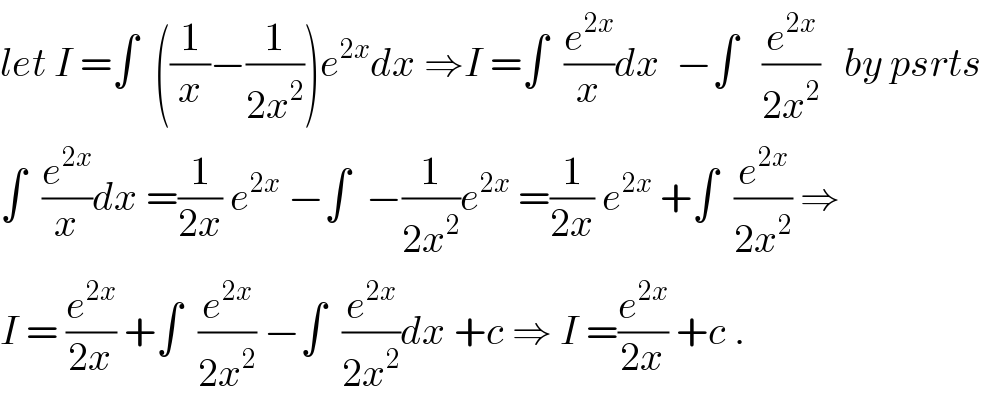
Commented by rahul 19 last updated on 10/Feb/19

thank you profAbdo .

Commented by maxmathsup by imad last updated on 11/Feb/19

$$youarewelcomesir.$$

Answered by kaivan.ahmadi last updated on 09/Feb/19

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{2}{\mathrm{x}}\Rightarrow \mathrm{f}\left(2\mathrm{x}\right)=\frac{1}{\mathrm{x}}\Rightarrow {\mathrm{f}}^{\prime }\left(\mathrm{x}\right)=\frac{-2}{{\mathrm{x}}^2}\Rightarrow$$$${\mathrm{f}}^{\prime }\left(2\mathrm{x}\right)=\frac{-1}{{2\mathrm{x}}^2}$$$$\int {\mathrm{e}}^{2\mathrm{x}}(\frac{1}{\mathrm{x}}-\frac{1}{{2\mathrm{x}}^2})\mathrm{dx}={\mathrm{e}}^{2\mathrm{x}}\mathrm{f}\left(2\mathrm{x}\right)+\mathrm{c}=\frac{{\mathrm{e}}^{2\mathrm{x}}}{\mathrm{x}}+\mathrm{c}$$$$$$$$$$$$$$

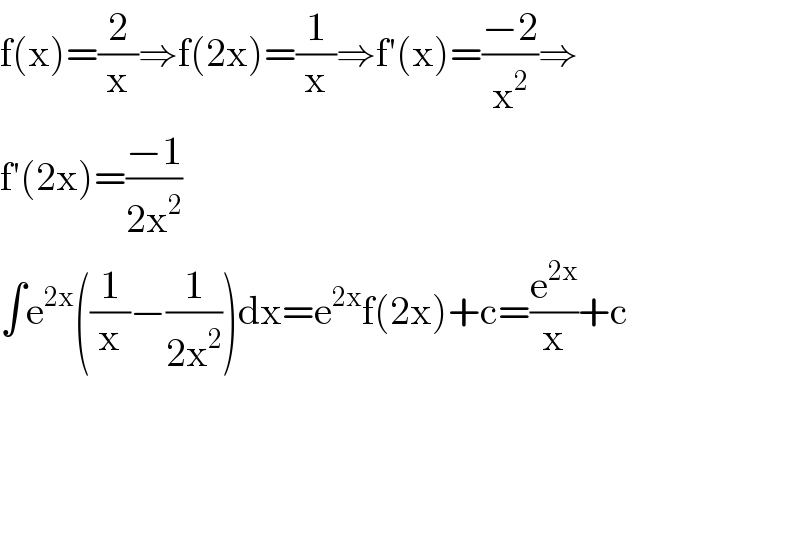
Commented by rahul 19 last updated on 09/Feb/19

$$Sir,iff\left(2x\right)=\frac{1}{x}thenf{}^{\prime }\left(2x\right)shouldbe$$$$\frac{-1}{x^2}?{Isn}^{\prime }tit?$$

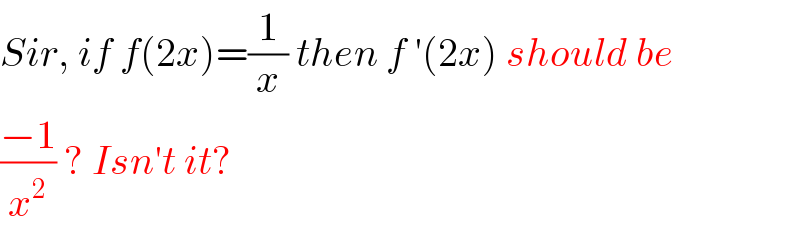
Commented by kaivan.ahmadi last updated on 09/Feb/19

$$\mathrm{yes}\mathrm{it}\mathrm{is},\mathrm{thank}\mathrm{you}.\mathrm{the}\mathrm{answer}\mathrm{of}\mathrm{your}\mathrm{integral}\mathrm{is}\mathrm{not}\mathrm{true},\mathrm{because}$$$${\left({\mathrm{e}}^{\mathrm{kx}}\mathrm{f}\left(\mathrm{kx}\right)\right)}^{{}^{\prime }}={\mathrm{ke}}^{2\mathrm{x}}(\mathrm{f}\left(\mathrm{kx}\right)+{\mathrm{f}}^{\prime }\left(\mathrm{kx}\right))$$$$$$$$$$$$$$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Feb/19

$$1)\frac{1}{2}\int [\frac{1}{x}\times \frac{d}{dx}\left(e^{2x}\right)+e^{2x}\frac{d}{dx}\left(\frac{1}{x}\right)]dx$$$$\frac{1}{2}\int \frac{d}{dx}\left(\frac{1}{x}{e}^{2x}\right)dx$$$$\frac{1}{2}\left(\frac{e^{2x}}{x}\right)+c$$$$2)\int e^{2x}\left(\frac{1+2sinxcosx}{2{cos}^{2}x}\right)$$$$\int e^{2x}(\frac{1}{2}{sec}^{2}x+tanx)dx$$$$\frac{1}{2}\int [e^{2x}\times \frac{d}{dx}\left(tanx\right)+tanx\times \frac{d}{dx}\left(e^{2x}\right)]dx$$$$=\frac{1}{2}\int \frac{d}{dx}\left(e^{2x}tanx\right)dx$$$$\frac{e^{2x}tanx}{2}+c$$

Commented by rahul 19 last updated on 10/Feb/19

thank you sir �� but how to do by using given formulae ?

Terms of Service

Privacy Policy

Contact: info@tinkutara.com